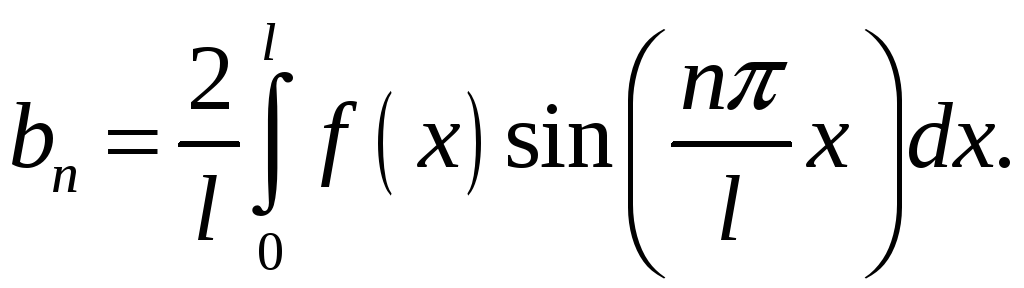Шпаргалка. Ряди

Типові ряди:

1. Геометрична прогресія: 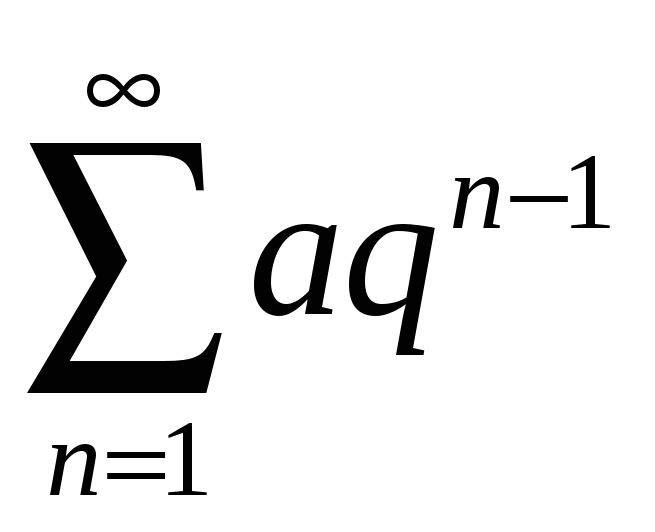, при : ряд збіжний і 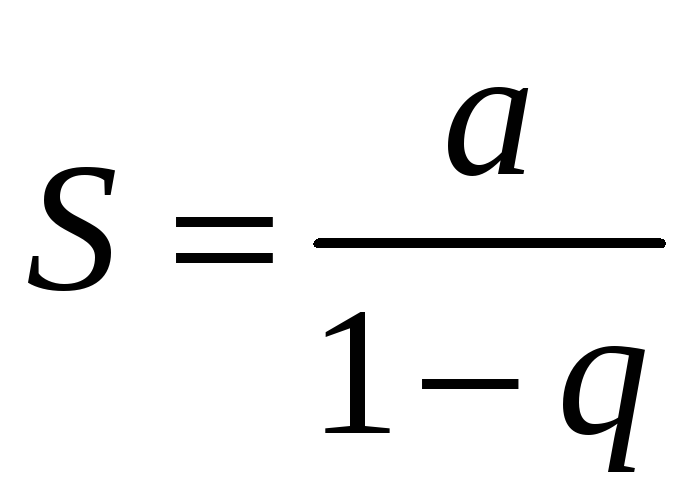, при : ряд розбіжний.

2. Гармонійний ряд: - ряд розбіжний.

3. Ряд Дирихле: , при : ряд розбіжний і при : ряд збіжний.

Необхідна ознака збіжності рядів: . Якщо необхідна ознака не виконується, то ряд розбіжний, якщо виконується: ряд потрібно далі досліджувати.

К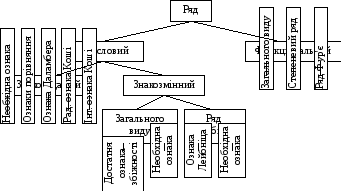ласифікація рядів

Достатні ознаки збіжності знакододатніх рядів:

1.Ознаки порівняння:

Ряд порівнюємо із рядом збіжність якого ми знаємо

а) перша ознака порівняння: якщо ряд збіжний і , то ряд також збіжний;

б) друга ознака порівняння: якщо ряд розбіжний і , то ряд також розбіжний;

в) гранична ознака порівняння: якщо 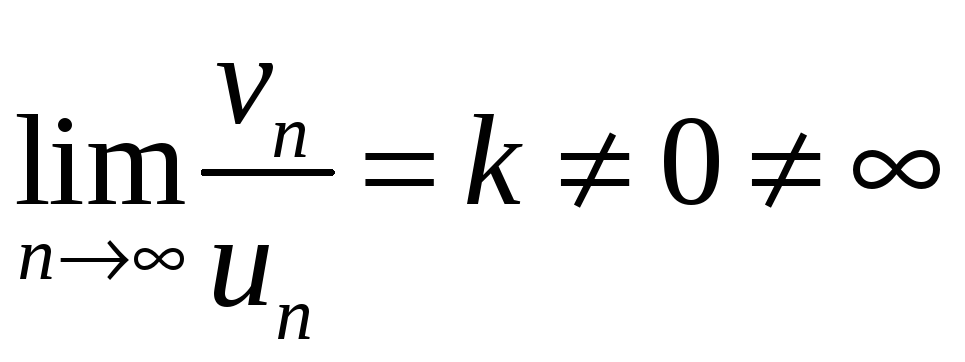, то ряди і збіжні або розбіжні одночасно.

2. Ознака Даламбера: якщо 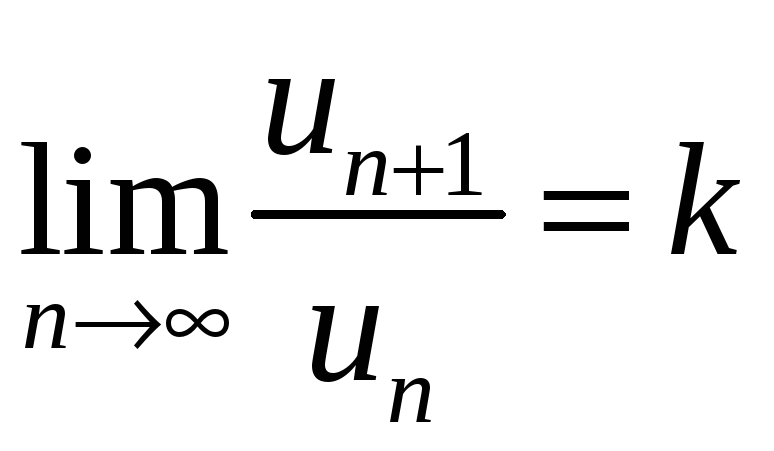, то при - ряд розбіжний, - ряд збіжний, при - ряд потрібно досліджувати далі.

3. Радикальна ознака Коші: якщо , то при - ряд розбіжний, - ряд збіжний, при - ряд потрібно досліджувати далі.

4. Інтегральна ознака Коші: якщо для ряда , , - неперервна на проміжку , то інтеграл і ряд збіжні або розбіжні одночасно.

Схема дослідження знакододатніх рядів

1. Візуально оцінити виконання необхідної умови збіжності рядів. Якщо загальний член є часткою многочленів або ірраціональних виразів, то необхідна умова не виконується, якщо старший степінь чисельника більше або дорівнює старшому степеню знаменника. Якщо необхідна умова не виконується, то ряд є розбіжним і відповідний висновок необхідно записати. Якщо необхідна умова виконується, то необхідно продовжити дослідження.

2. Якщо загальний член є часткою многочленів або ірраціональних виразів, то необхідно використати граничну ознаку порівняння із рядом Дирихле , де - різниця між старшим степенем знаменника і старшим степенем чисельника.

3. Якщо загальний член ряду містить факторіал чи інший добуток членів деякої послідовності, то необхідно використати ознаку Даламбера.

4. Якщо загальний член ряду можна представити у вигляді , то використовується радикальна ознака Коші.

5. Якщо загальний член ряду можна представити у вигляді 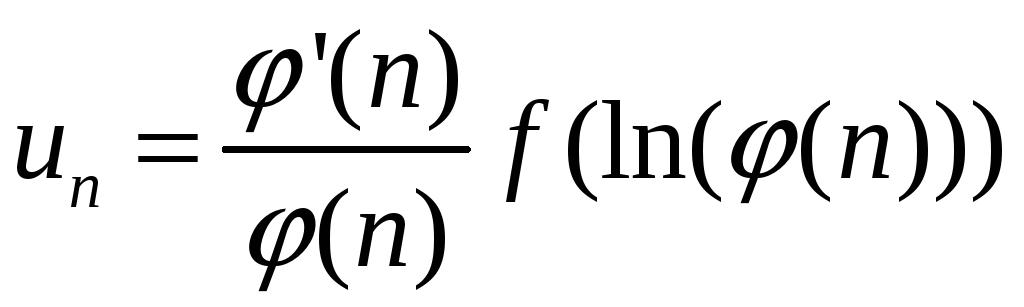або , де - функція, від якої береться інтеграл, то використовується інтегральна ознака Коші

6. Якщо жодна рекомендація не підходить, то перебирають послідовно усі ознаки починаючи із ознаки Даламбера. Далі можна спробувати граничну ознаку порівняння із рядом Дирихле , де вибирають за умови рівності границі 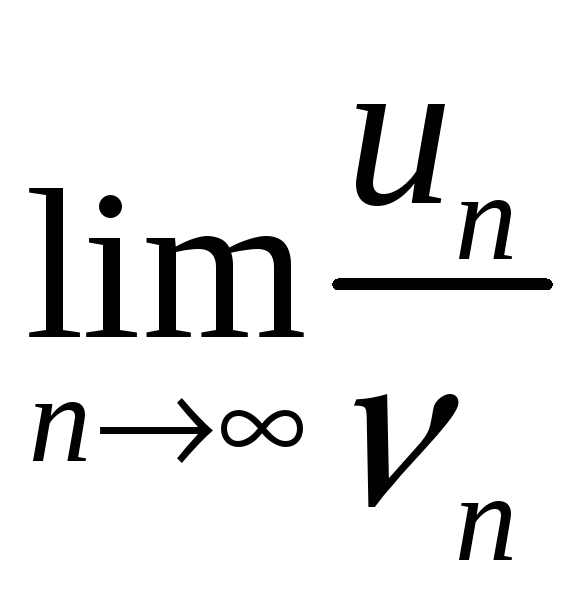числу . Також потрібно не забути про необхідну ознаку збіжності і розглянути її більш уважно.

Схема дослідження знакозмінних рядів загального виду

1. Складаємо ряд із модулів членів знакозмінного ряду. Якщо отриманий знакододатній ряд збіжний, то і сам знакозмінний ряд абсолютно збіжний. Якщо ряд з модулів розбіжний – то знакозмінний ряд потрібно далі досліджувати.

2. Перевіряємо виконання необхідної ознаки збіжності. Якщо не виконується – ряд розбіжний, якщо виконується – потрібно досліджувати далі.

Схема дослідження рядів Лейбніца

1. Досліджуємо ряд за ознакою Лейбніца, яка має дві умови:

а)

б) , де (здебільшого - загальний член ряду без ).

Якщо обидві умови виконуються, то ряд збіжний. Якщо друга умова не виконується, то автоматично не виконується необхідна ознака збіжності рядів і ряд є розбіжний.

2. Якщо ряд збіжний, то він може бути абсолютно збіжним або умовно збіжним. Для дослідження на умовну та абсолютну збіжність потрібно скласти ряд із модулів членів ряду (здебільшого загальний член цього ряду дорівнює загальному члену ряду Лейбніца без ). Якщо отриманий ряд збіжний, то сам ряд Лейбніца абсолютно збіжний, якщо ряд з модулів розбіжний – то ряд Лейбніца умовно збіжний.

Схема визначення області збіжності степових рядів

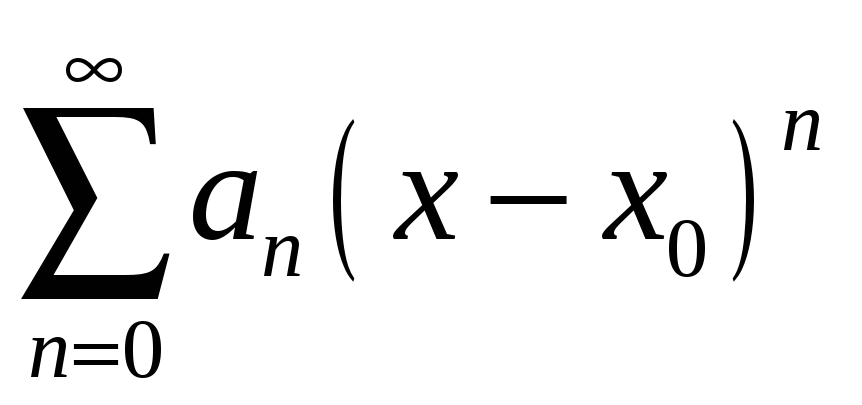
1. Область збіжності:

2. - визначаємо безпосередньо із загального виду ряду. Якщо степеневий ряд виду 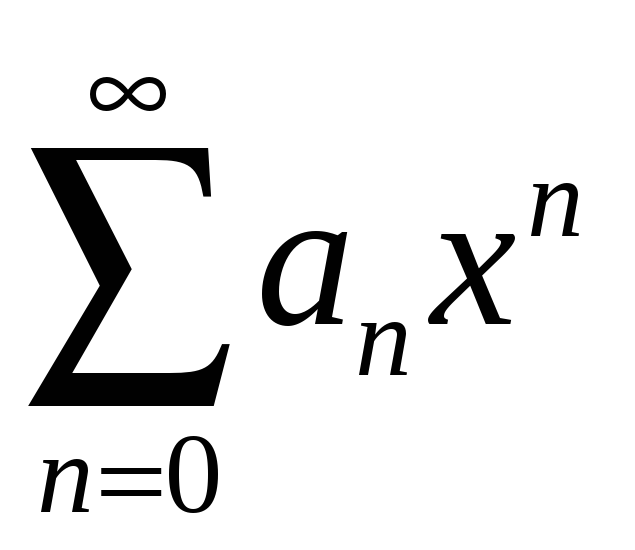, то .

3. Радіус збіжності визначаємо за однією з формул:

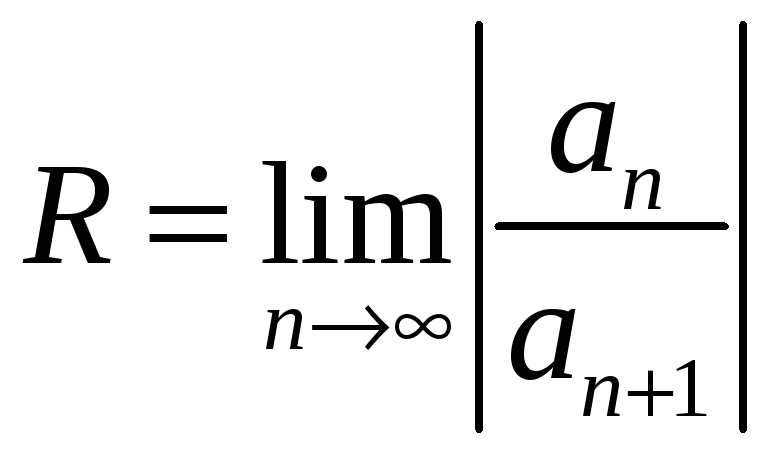або .

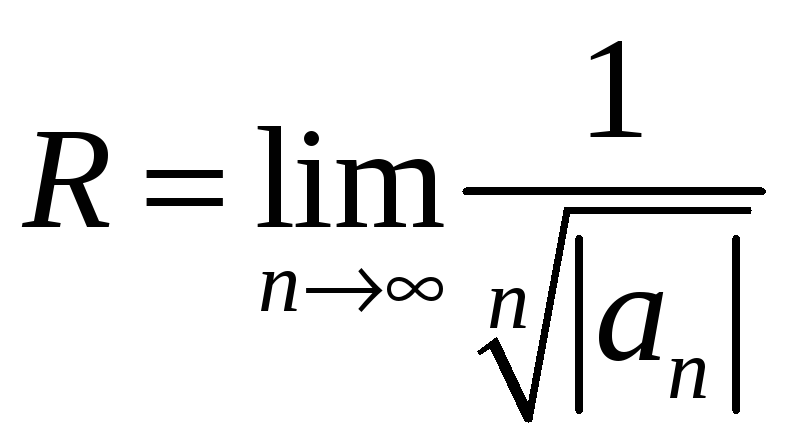4. Досліджуємо ряд на кінцях інтервалу збіжності.

Наближене обчислення суми ряду із точністю

, де - вибирають з умови

Наближене обчислення суми ряду Лейбніца із точністю

, де - вибирають з умови

Розклад функцій у ряд Тейлора

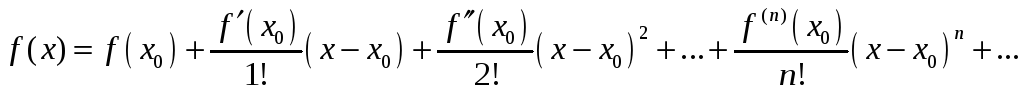
Розклад функцій у ряд Маклорена

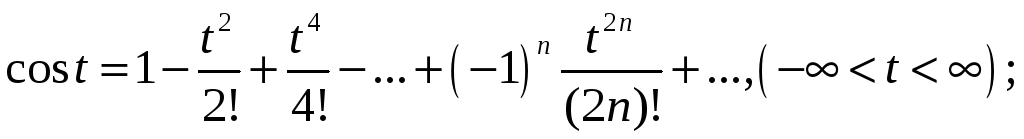
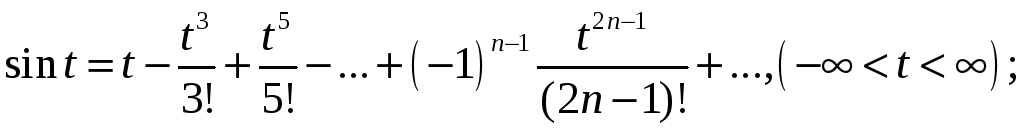
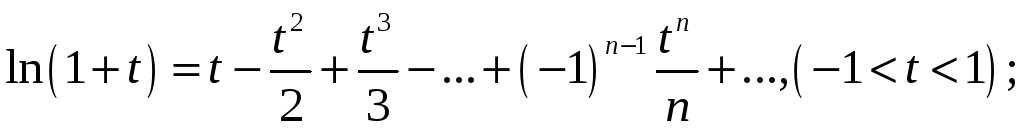
Ряди Фур'є

Для -періодичної функції:

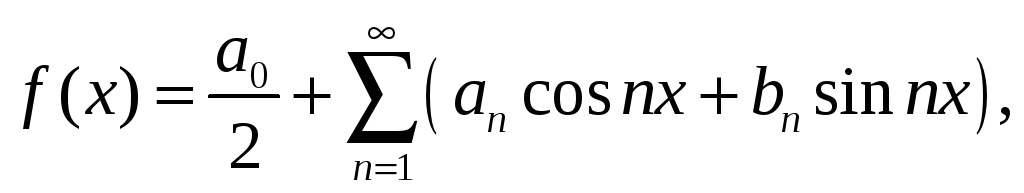
де

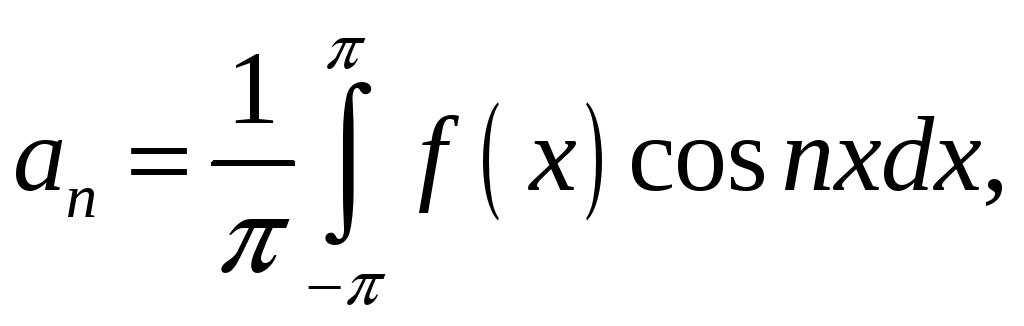
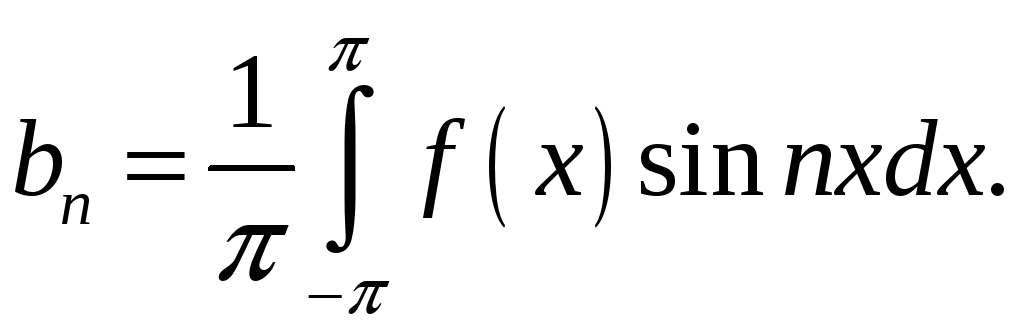
Для -періодичної функції:

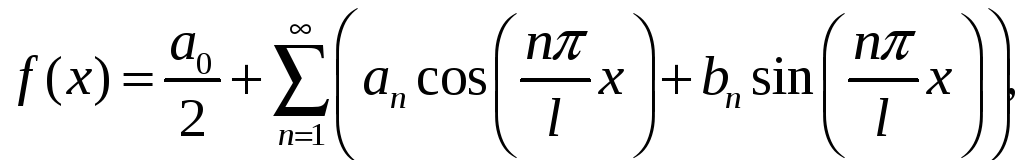
де

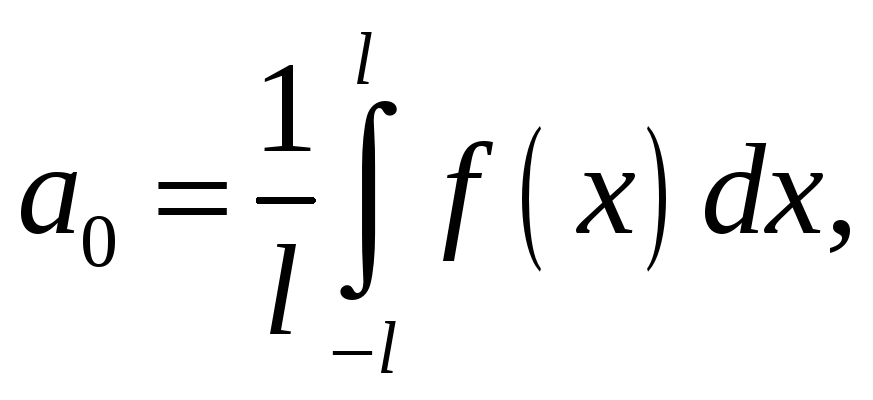
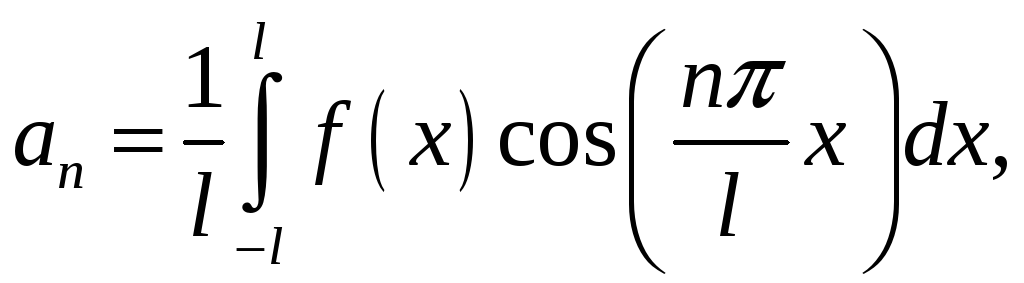
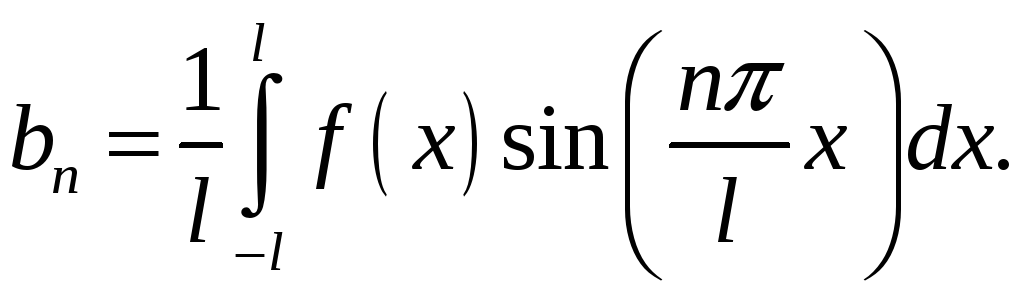
Для парної -періодичної функції:

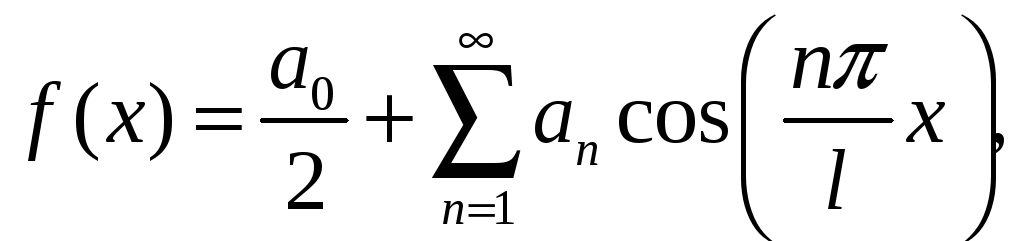
де

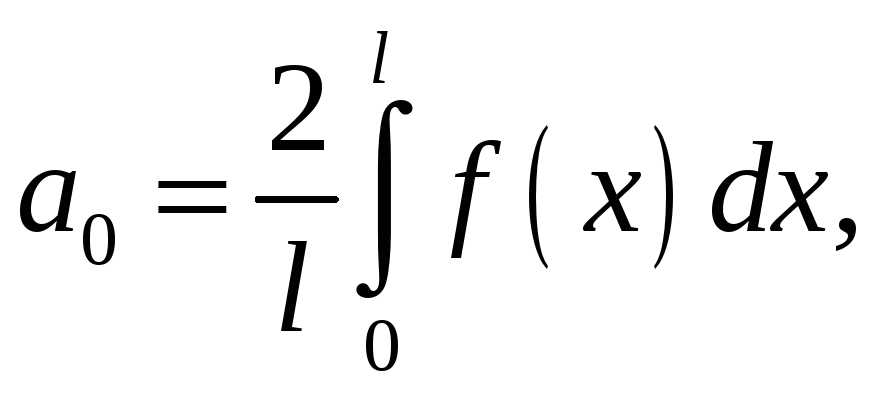
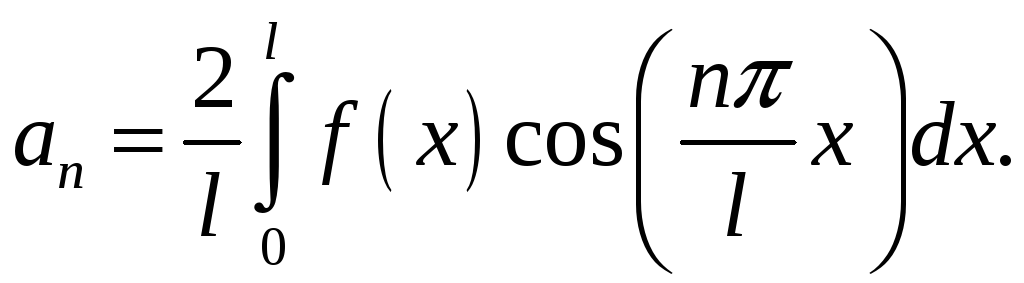
Для непарної -періодичної функції:

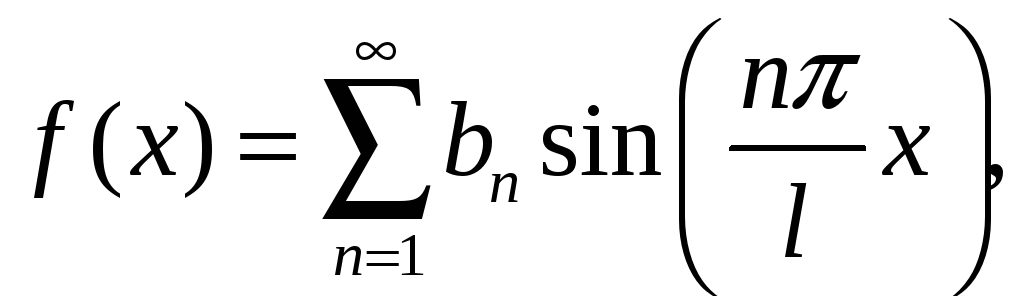
де