Коливання струни
Коливання тонкої пружної струни описуються одновимірним хвильовим рівнянням. Граничні умови полягають у рівності нулю переміщень закріплених кінців струни. Початкові умови визначаються амплітудою і положенням точки, у якій струну відтягнули у нульовий момент часу. Припустимо, струна має довжину 70 см і її відтягнули на 0,1 см у точці, віддаленій на 20 см від одного кінця. У такому випадку початкові умови будуть мати такий вигляд:
;
.
Для стійкості різницевої схеми коефіцієнт у різницевому рівнянні повинен дорівнювати 1
.
Заміна цього коефіцієнта одиницею також спрощує саме різницеве рівняння
.
Сила
натягу струни визначає швидкість хвилі,
яка біжить у ній, що у свою чергу задає
співвідношення між кроками за часом і
за просторовою координатою. Наприклад,
якщо розтягання
струни задає швидкість хвилі, рівну
см/с, кроки за часом і простором будуть
співвідноситися так
.
Оскільки
крок по просторовій координаті
складає
10см, то крок за часом
повинен
дорівнювати
с.
З початкових умов відомо, що в нульовий момент часу струну відтягнули на деяку величину, не додаючи початкової швидкості. Тому значення функції на першому кроці повинне дорівнювати її значенню в момент
.
Внесемо це значення в різницеве рівняння для першого кроку
.
Хід роботи
Побудуємо таблицю для розрахунку коливань струни, описуваних приведеними співвідношеннями.
Створіть новий лист і назвіть його ЛР№ 17.
Включіть режим автоматичного перерахування сторінки.
Виділіть стовпці В:М і зробіть їхню ширину рівною 6. Ширину стовпця А зробіть рівною 9.
В комірці А1 введіть заголовок Коливання струни; гіперболічне рівняння.
В комірці С2 введіть заголовок Зміщення відтягнутої струни.
Введемо в таблицю значення моментів часу з кроком 210–4с і просторові координати вузлів сітки з кроком 10 см.
В комірці А3 введіть заголовок Час і вирівняйте його по центру.
В комірці А4 введіть напис (с) і вирівняйте його по центру.
В комірці А5 введіть 0, а в комірці А6 – 0,0002; виділіть комірки А5:А6 і перетягніть маркер заповнення в комірку А35.
Зробіть формат комірок А5:А35 експонентним з одною цифрою після коми.
В комірці В3 введіть заголовок Гр. умови і вирівняйте його по центру.
В комірці Е3 введіть заголовок Довжина (см).
В комірці B3 уведіть заголовок Гр. умови і вирівняйте його по центру.
Введіть в комірці В4 значення 0, в комірці С4 – значення 10; виділіть комірки В4:С4 і перетягніть маркер заповнення в комірку I4.
Введемо в таблицю початкові умови для струни, відтягнутої на 0,1см у точці, яка знаходиться на 20 см від кінця. Значення переміщень змінюються від зазначеної точки до кінців струни за лінійним законом.
Введіть у зазначених комірках таки значення:
B5 – 0 |
C5 – 0,05 |
D5 – 0,1 |
E5 – 0,08 |
F5 – 0,05 |
G5 – 0,04 |
H5 – 0,02 |
I5 – 0 |
J5 – Поч. умови |
Введемо в таблицю граничні умови уздовж її бічних стовпців.
В комірці В6 введіть формулу =В5 і скопіюйте її в комірки В7:В35.
В комірці I6 введіть формулу =I5 і скопіюйте її в комірки I7:I35.
Введемо в таблицю спеціальне різницеве рівняння для першого кроку, що містить передбачуване значення шуканої функції на першому кроці.
В комірці С6 введіть формулу =0,5*(В5+В5) і скопіюйте її в комірки D6:Н5.
Завершимо побудову таблиці, вносячи в неї стандартне різницеве рівняння.
В комірці С7 введіть формулу =В6+В6-С5 і скопіюйте її в комірки С8:Н35.
Зробіть формат комірок В5:Н35 числовим із двома значущими цифрами після коми
Побудована таблиця повинна виглядати так, як на рис. 29.
Якщо простежити зміни в положенні струни, можна помітити, що вона коливається з періодом 2,810–3c або частотою 357 Гц. Аналітичний вираз для частоти коливань дає той же результат
Гц,
де f – частота,
l – довжина струни.
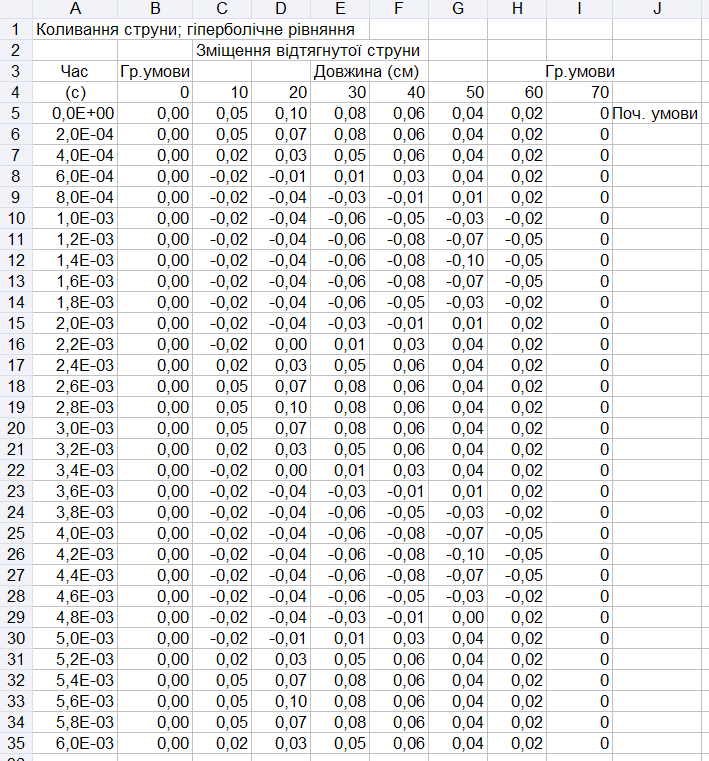
Рисунок 29