Контрольні питання

1. У чому сутність методу простої ітерації?

2. Яка умова збіжності ітераційного процесу?

3. Як виглядає ітераційний процес при 0<<1, якщо x₀<?

4. Як виглядає ітераційний процес при 0<<1, якщо x₀>?

5. Як виглядає ітераційний процес при –1<<0?

6. Як виглядає ітераційний процес при >1?

7. Як виглядає ітераційний процес при <–1?

2 Розв’язання алгебраїчних рівнянь вищих стЕпе­нів і трансцендентних рівнянь методом Ньютона

Мета роботи – вивчення ітераційних методів і набуття навичок розв'язання нелінійних алгебраїчних і трансцендентних рівнянь методом Ньютона із застосуванням Microsoft Excel'2000.

План проведення роботи

1. Відповідно до порядкового номера бригади студентів в журналі академгрупи виписати рівняння з таблиці 2.

2. Розв'язати рівняння методом Ньютона з точністю  = 10^–5.

3. Зробити висновки.

Таблиця 2

Варіант	Рівняння	Відрізок, що містить корінь
	sin x – x*cos x = 0	[4; 5]
		[0,8; 1,6]
		[2,5; 4,0]
		[0,5; 2,0]
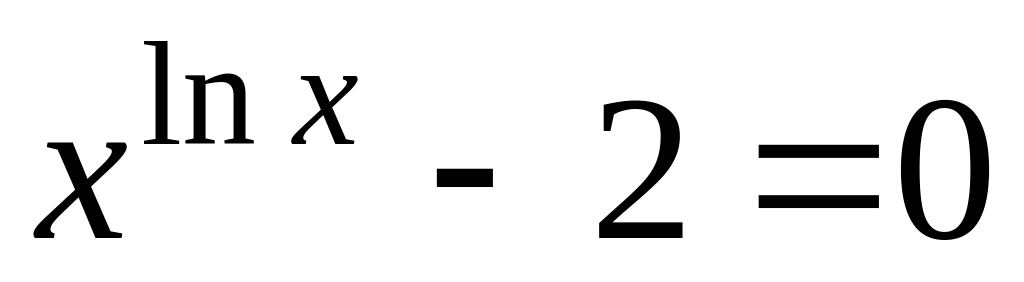
		[1,5; 3,0]
		[2; 3]
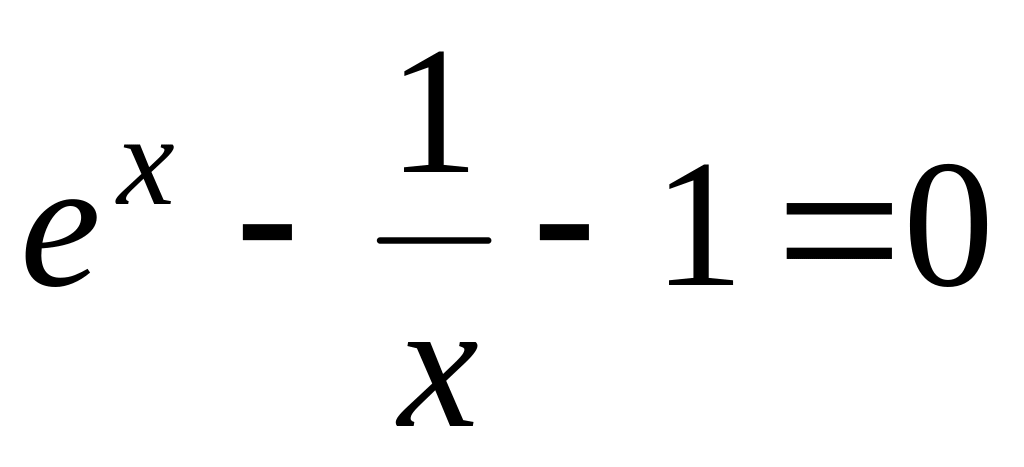
		[0,5; 1]
		[0,2; 1,0]
		[2,8; 3,2]
	– cos (1 – x) = 0	[0,5; 2]

Хід роботи

Для застосування методу Ньютона перепишемо рівняння в неявній формі

F(x) = cos(x) – x = 0.

Потім розрахуємо похідну функції, яка стоїть в лівій частині рівняння.

F'(x) = – sin(x) –1.

Для розв’язання рівняння необхідно.

1. Відкрити новий робочий лист та назвати його ЛР№2.

2. Вибрати команду Сервис=>Параметры. Відкрити вкладку Вычисления включити режим Вручную зробити значення поля Предельное число итераций рівним 1 та заберіть відмітку з перемикача Пересчет перед сохранением. Натисніть кнопку ОК (Рис. 3).

3. Зробити ширину стовпця А рівною 38.

4. Ввести в комірку А1 текст cos(x) – x = 0; метод Ньютона.

5. В комірки А3:В4 ввести наведені нижче значення. Вирівняти вправо вміст комірок А3:А4.

Комірка	Значення	Комірка	Значення
А3	Поч. значення	В3	0
А4	Поч. прапорець	В4	ИСТИНА

В комірці В6 буде виконуватись перевірка чи рівна ИСТИНА значенню комірки В4. Якщо це так, х буде встановлено рівним початковому значенню, а в іншому випадку – рівним комірці В9, тобто x₀–F(x₀)/F'(x₀).

6. Введіть вказані нижче значення та формули в комірки А6:В9. Вирівняйте вправо їх зміст.

Комірка	Значення	Комірка	Формула
А6		В6	= ЕСЛИ(В4;В3;В9)
А7		В7	= COS(B6)-B6
А8		В8	= –SIN(B6) – 1
А9		В9	= B6–B7 / B8

7. В комірку А11 введіть текст Похибка та вирівняйте її по правому краю.

8. В комірку В11 введіть формулу = В9-В6.

7. Перетворіть комірку В9 в експоненціальний формат з двома цифрами після коми.

Тепер організуємо друге циклічне посилання – для підрахунку кількості ітерацій.

10. В комірку А13 введіть Ітерації та вирівняйте її по правому краю.

11. В комірку В13 введіть =ЕСЛИ (В4;0;В14+1).

12. В комірку В14 введіть =В13

13. Відключіть лінії сітки.

14. Для виконання обчислювання встановіть значення початкового прапорця в комірці В4 рівним ИСТИНА та натисніть клавішу <F9> (Вычислить) для запуску процесу розв’язання задачі.

15. Змініть значення початкового прапорця на ЛОЖЬ та знову натисніть клавішу <F9>.

При кожному натисканні клавіші <F9> виконується одна ітерація та обчислюється наступне приблизне значення х.

16. Натискайте клавішу <F9> до тих пір, поки значення х не досягне необхідної точності.

Точність отриманого приблизного значення х₀ перевіряється шляхом його порівняння із значенням х₁; різниця між ними відображається в комірці В11. До цього моменту робочий лист повинен виглядати так, як на рис. 4. Значення х яке є коренем рівняння, наведене в комірках В6 та В9.