Контрольні питання

1. Класифікація методів розв’язання диференціальних рівнянь у частинних похідних.

2. Постановка задачі розв’язання диференціальних рівнянь у частинних похідних.

3. Сутність скінченнорізницевого методу розв’язання рівнянь еліптичного типу.

4. Постановка задачі Діріхле для рівняння Пуасона.

5. Оцінювання похибки розв’язання рівнянь еліптичного типу.

15 Розв’язання параболічних рівнянь у частинних похідних методом послідовного обчислення таблиці значень

Мета роботи – надбання практичних навичок розв'язання параболічних рівнянь у частинних похідних методом послідовного обчислення таблиці значень із застосуванням Microsoft Excel.

План роботи

1. Відповідно до порядкового номера бригади студентів в журналі академгрупи вибрати рівняння з таблиці 17.

2. Розв'язати рівняння теплопровідності 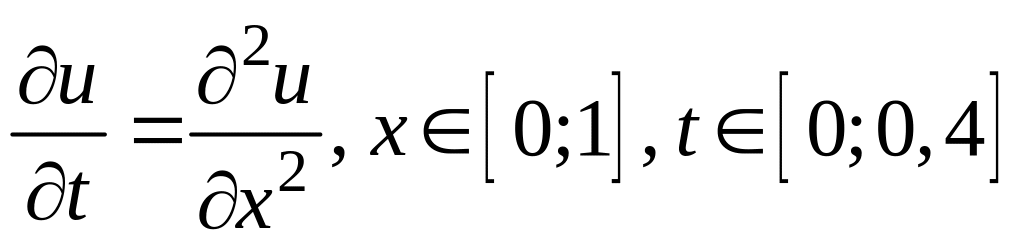з початковою умовою u(x;0)=f(x), 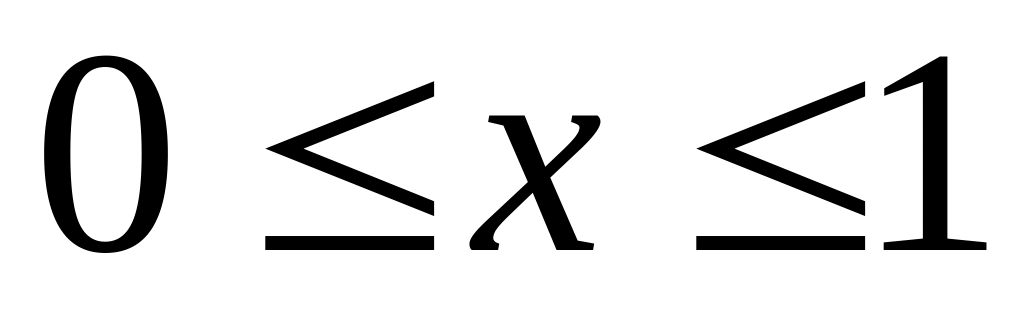і крайовими умовами u(0; t) = a, u(1; t) = b з точністю  = 10^–5.

3. Зробити висновки.

Таблиця 17

Варіант	f(x)	a	b	c
		1,1	3,0	0,05
		1,2	3,5	0,15
		1,3	4,0	0,25
		1,4	4,5	0,35
		1,5	5,0	0,45
		1,6	5,5	0,55
		1,7	6,0	0,65
		1,8	6,5	0,75
		1,9	7,0	0,85
		2,0	8,0	0,95

Короткі теоретичні відомості

Лінійне рівняння в частинних похідних другого порядку називається параболічним, якщо його дискримінант, тобто комбінація коефіцієнтів , дорівнює нулю. Параболічні рівняння звичайно виникають у задачах, пов'язаних з дифузією і плином рідини. Як правило, такі рівняння містять першу похідну за часом і другу похідну за просторовою координатою від концентрації будь-якої скалярної фізичної величини (щільності заряду, температури, концентрації хімікату і т.п.). Найбільш важливим з цих рівнянь є рівняння нерозривності.

Рівняння нерозривності

Рівняння нерозривності в загальному вигляді – це математичний запис закону збереження маси або твердження про те, що швидкість зміни концентрації фізичної величини у певному об’ємі дорівнює швидкості припливу величини в об’єм мінус швидкість витоку її з об’єму, плюс інтенсивність генерування цієї величини в об’ємі і мінус інтенсивність її поглинання там же. Якщо позначити швидкість потоку цієї величини через , одержимо таке рівняння в частинних похідних

.

Тут дивергентний член (перший доданок у правій частині) описує приплив і виток величини в нескінченно малому об’ємі, доданок G описує генерування, А – поглинання щільності.

Рівняння нерозривності широко поширене у фізиці і техніці, будучи досить загальним для опису різного роду процесів. Рух усякої речовини або фізичної величини, що може переміщатися у відведеному об’ємі, описується, у числі інших співвідношень, рівнянням нерозривності. Загальний вигляд рівняння залишається, як правило, одним і тим же для всіх фізичних субстанцій.