8 Розв’язання звичайних диференціальних рівнянь методами Ейлера
Мета роботи – ввчити наближені методи розв’язання звичайних диференціальних рівнянь методами Ейлера та набути навичок їх розв'язання із застосуванням Microsoft Excel'2000.
План роботи
Виписати з таблиці завдань диференціальне рівняння, початкове та кінцеве значення незалежної змінної, значення функції
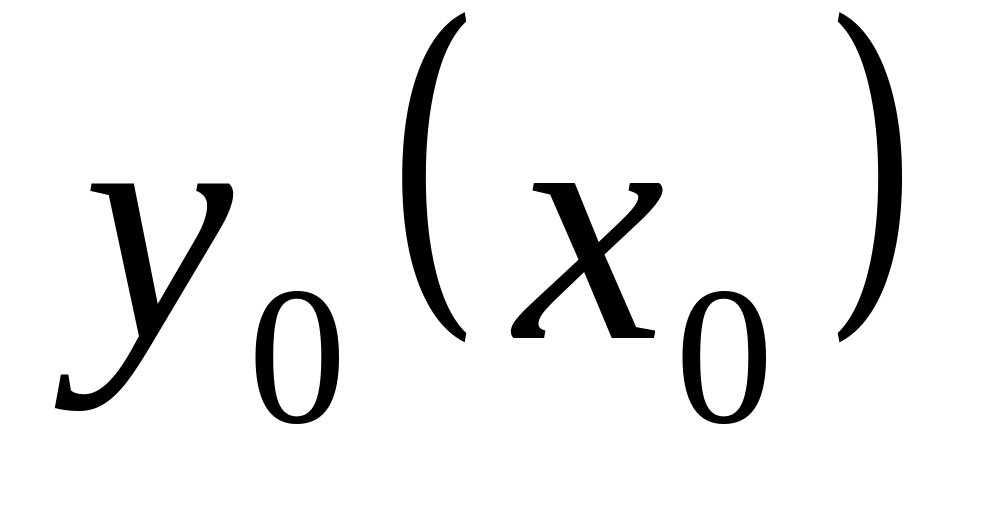при відомому значенні аргументу
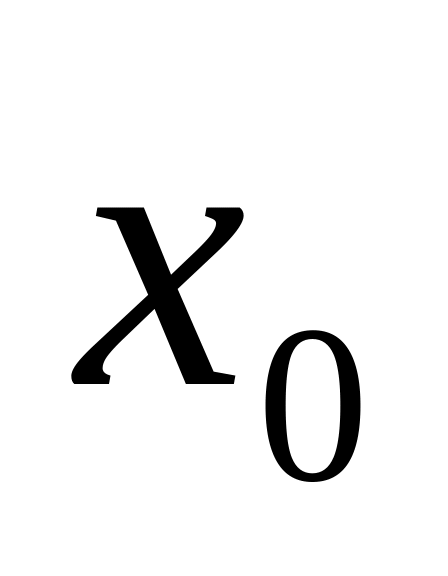згідно з номером бригади студентів в
журналі академгрупи.За правилом Рунне визначити шаг інтегрування, якій задовольняє заданої точності .
Розв'язати рівняння методом Ейлера та модифікованим методом Ейлера.
Проаналізувати отримані результати рішення та оцінити їх похибку.
Таблиця 9
Варіант |
Диференціальне рівняння |
Інтервал |
|
Точність |
|
1 |
|
0 |
1 |
0,12 |
0,0002 |
2 |
|
0 |
1,2 |
0 |
0,00005 |
3 |
|
0 |
0,7 |
0 |
0,0005 |
4 |
|
2 |
4 |
2 |
0,002 |
5 |
|
0 |
0,8 |
5,6 |
0,0002 |
6 |
|
1 |
2 |
3,54 |
0,02 |
7 |
|
2 |
3,5 |
0,12 |
0,002 |
8 |
|
0 |
2 |
0,8 |
0,001 |
9 |
|
3 |
4 |
2,15 |
0,0008 |
10 |
|
0,5 |
2 |
0 |
0,0005 |
Хід роботи
Розглянемо таке звичайне диференціальне рівняння першого порядку
з початковою умовою u(0) = 0.
Метод Ейлера дозволяє усунути необхідність в обчисленні похідних завдяки урізанню ряду Тейлора до члена з першою похідною. Для того щоб це спрацювало необхідно вибирати малі значення h та після кожного кроку перераховувати значення першої похідної на початку нового малого інтервалу
Розв’яжемо диференціальне рівняння методом Ейлера на листі електронної таблиці.
Створіть новий робочий лист та назвіть його ЛР№ 8.
Введіть в комірку А1 текст Звичайні диференціальні рівняння; методи Ейлера.
В комірки А3 введіть текст х, а в комірку В3 – u(x).
В комірку А5 введіть значення 0, а в комірку А6 введіть 0,01, виділіть комірки А5:А6 та перетягніть маркер заповнення в комірку А25.
Знайдемо чисельне розв’язання рівняння методом Ейлера.
5. В комірці В4 введіть За Ейлером.
6. В комірці В5 введіть 0.
7. В комірці В6 введіть таку формулу =В5+(A6-A5)*(A5-В5) /КОРЕНЬ(1+A5^2) та скопіюйте її в комірки В7:В25.
Оскільки на початку кожного кроку для визначення значення шуканої функції на другому кінці інтервалу береться приблизне значення похідної, яке до того ж підставляється в грубе наближення для ряду Тейлора, за ходом інтегрування неперервно зростає та накопичується похибка. Більш прийнятним способом є отримання значення функції з використанням середнього на кроці значення похідної
Складність застосування цієї модифікації методу полягає в тому, що похідна на дальньому кінці інтегралу невідома. В модифікованому методі Ейлера (методі «предиктор-коректор» або «передбачення-уточнення») для початкового значення функції використовують звичайний метод Ейлера. З використанням цього положення обчислюється похідна на дальньому кінці інтервалу. Маючи значення похідної на початку та оцінку її значення в кінці інтервалу, можна точніше оцінити значення шуканої функції. Для уточнення отриманого значення можна застосувати даний метод ще раз, але при великій кількості ітерацій похибка методу перекриває будь-які поправки в точності.
Перерахуємо лист таблиці модифікованим методом Ейлера. Спочатку обчислимо перше наближення до розв’язання, використовуючи звичайний метод Ейлера.
Введіть в комірку С3 текст Модиф. метод Ейлера.
Виділіть комірки Е3:D3 та клацніть на кнопці Объединить и поместить в центре на панелі інструментів EXСEL.
В комірку С4 введіть ПРЕДИКТОР та вирівняйте надпис по центру комірки.
В комірці С5 введіть таку формулу =D5+(A6-A5)*(A5-D5)/ КОРЕНЬ(1+A5^2) та скопіюйте її в комірки C6:C24.
Отримане початкове наближення (предиктор) буде використовуватися для обчислення похідної в проміжній точці та обчислення скоректованого значення (коректора ) шуканої функції.
В комірку D4 введіть КОРЕКТОР та вирівняйте надпис по центру комірки.
В комірці D5 введіть 0.
В комірці D6 введіть таку формулу =D5+((A6-A5)/2)*((A5-D5)/ КОРЕНЬ(1+A5^2)+(A6-С5)/КОРЕНЬ(1+A6^2)) та скопіюйте її в комірки D7:D25
Зробіть формат комірок C5:D25 експоненціальним з двома значущими десятковими цифрами.
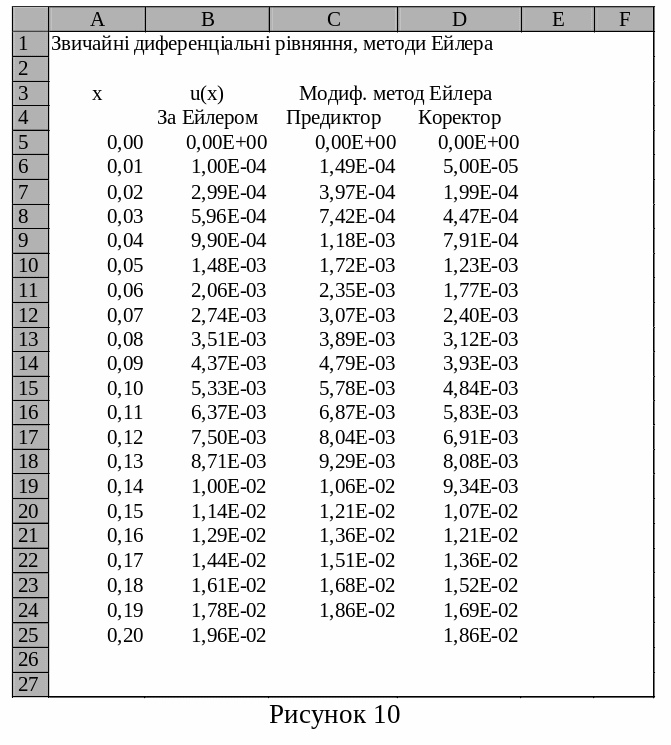
В результаті виконаних дій електронна таблиця повинна мати такий вигляд, як на рис. 10.
