Контрольні питання
В чому полягає задача чисельного диференціювання?
Як знайти помилку чисельного диференціювання?
Як використовуються для чисельного диференціювання скінченні різниці?
Яку похибку має ліва різницева формула?
Яку похибку має права різницева формула?
Яку похибку має центральна різницева формула?
7 Чисельне інтегрування Мета роботи – вивчити чисельні методи обчислення визначених інтегралів та набути навичок обчислення визначених інтегралів із застосуванням Microsoft Excel'2000. План роботи
Відповідно до порядкового номера бригади студентів в журналі академгрупи виписати підінтегральну функцію з таблиці 8.
Обчислити визначений інтеграл за формулами прямокутників, трапецій, Ромберга і Симпсона.
Зробити висновки.
Таблиця 8
-
Варіант
Підінтегральна функція
Межі
нижня
верхня
1
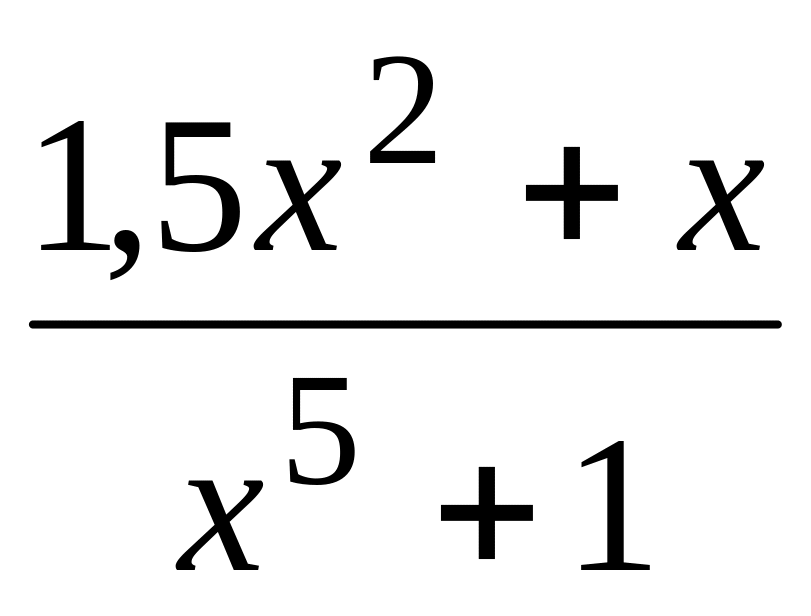
0
1,2
2
2
4,4
3
1
2,2
4
0
1,2
5
0
1,2
6
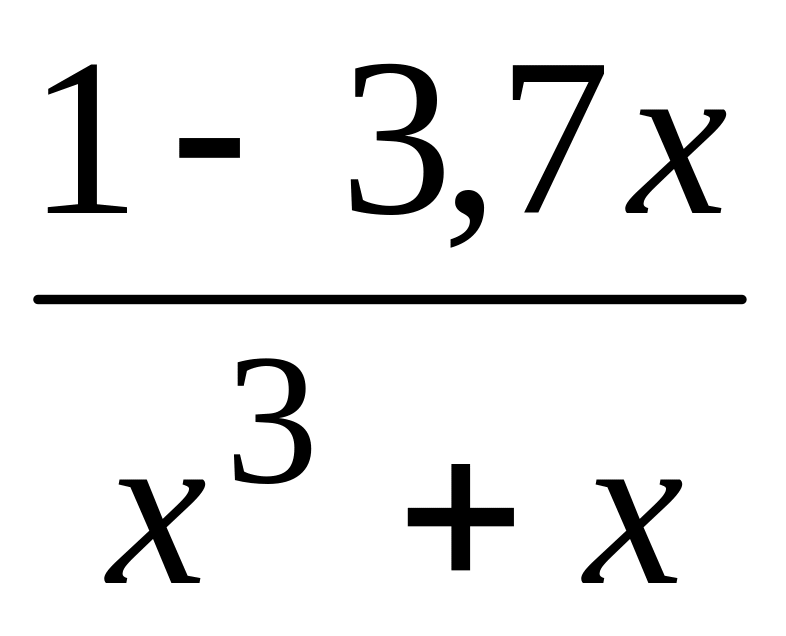
2
4,4
7
1
2,8
8
1
3,4
9
1
2,2
10
0
1,8
Короткі теоретичні відомості
Інтегрування дискретних даних включає в себе апроксимацію цих даних відомою функцією із наступним її інтегруванням. В більшості випадків не вдається підібрати одну функцію для апроксимації на всьому інтервалі, причому область інтегрування розділяється на велику кількість підінтервалів, на кожному з яких використовується проста функція типу лінійної, квадратичної або кубічної. Після чого результати для окремих підінтервалів додаються разом для отримання повного інтеграла.
Найбільш часто при чисельному інтегруванні використовують формули прямокутників, правило трапецій, Ромберга, Сімпсона та Гауса. Кожен із цих методів є більш точним, ніж попередній, оскільки проводить апроксимацію даних більш складною кривою.
Формула прямокутників. Згідно з формулою прямокутників, область між точками заповнюється прямокутниками, висота яких відповідає координаті у одній із точок, а ширина дорівнює відстані між точками. Значення інтеграла визначається за такою формулою
Таке наближення може здаватися дуже грубим, однак при малій ширині інтервалу та гладкій функції результат отримується досить точним. Крім того, такий метод дуже просто реалізовувати, оскільки достатньо просто перемножити дані в кожній точці на ширину інтервалу та підрахувати результати.
Формула трапецій. Згідно з цією формулою, кожна пара сусідніх точок з'єднується прямою лінією, яка утворює послідовність трапецій. Площа трапеції дорівнює півсумі основи помноженої на висоту – відстань між точками в даному випадку. Загальний інтеграл дорівнює сумі площ всіх трапецій
Формула Ромберга. Інтегрування за формулою трапецій можна покращити за допомогою формули Ромберга, використовуючи дві різні оцінки для екстраполяції значення інтеграла. При обчисленні першої оцінки використовують формулу трапецій для кожної точки, а при обчисленні другої оцінки використовують правило трапеції для кожної другої точки.
Отримані оцінки відповідають різним інтервалам між точками. Згідно з методом Ромберга, похибка при обчисленні інтеграла пропорційна квадрату відстані між точками,
I = I1 + Ch2, I = I2 + C(2h2)2,
де С – постійна. Розв’язання цих двох рівнянь приводить до такого виразу для інтеграла
I = I1 +(I1 – I2)/3.
Формула Сімпсона. Згідно з формулою Сімпсона, для апроксимації даних використовують рівняння параболи за трьома точками (правило 1/3) чи за чотирьома точками (правило 3/8)
