§ 14. Смешанное произведение векторов

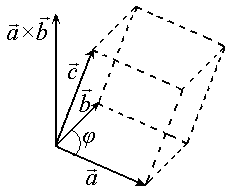
Смешанным (векторно-скалярным) произведением векторов , и называется скалярное произведение вектора × на вектор , т.е. ( × )∙ .

В силу определения скалярного произведения:

( × )∙ = | × | = (| |∙| | ) .

Свойства смешанного произведения:

1⁰. Смешанное произведение трех векторов равно нулю, если:

а) хоть один из перемножаемых векторов нулевой;

б) два из перемножаемых векторов коллинеарны;

в) три ненулевых вектора параллельны одной и той же плоскости или принадлежат одной плоскости.

2⁰. Смешанное произведение не изменится, если в нем поменять местами знаки векторного и скалярного произведений, т.е.

( × )∙ = ∙( × ).

В силу этого свойства смешанное произведение векторов , и можно записать в виде

.

3⁰. Смешанное произведение не изменится, если переставлять перемножаемые векторы в круговом порядке:

= = .

4⁰. При перестановке любых двух векторов смешанное произведение меняет знак:

= − , = − , = − .

Если известны координаты векторов , и :

= (а_х, а_у, a_z) = а_х + а_у + a_z , = (b_х, b_y, b_z) = b_х + b_y + b_z и

= (с_х, с_у, с_z) = с_х + с_у + с_z , то смешанное произведение векторов , и можно вычислить по формуле

= . (1)

Объем параллелепипеда, построенного на векторах , и :

V = | |. (2)

Объем пирамиды, построенной на векторах , и :

V = | |. (3)

Признак компланарности

Для того, чтобы три ненулевых векторы , и были компланарны, необходимо и достаточно, чтобы = 0.

Пример. Показать, что

( + )∙(( + )× ) = − .

□ Раскроем скобки:

( + )∙(( + )× ) = ( + )∙( × + × ) = ∙( × ) + ∙( × )+

+ ∙( × ) + ∙( × ).

Согласно свойству 2⁰ последнее выражение можно записать в виде

+ + + .

Здесь в первом слагаемом два коллинеарных вектора и , в третьем и четвертом слагаемых по два коллинеарных вектора. Значит, смешанные произведения , и равны нулю. Поэтому

( + )∙ (( + )× ) = .

По свойству 4⁰ имеем = − .

Окончательно,

( + )∙(( + )× ) = − . ■

§ 15. Линейный оператор

Если задан закон (правило), по которому каждому вектору линейного пространства Rⁿ ставится в соответствие единственный вектор линейного пространства R^m, то говорят, что задан оператор

(преобразование, отображение) А, действующий из Rⁿ в R^m, и записывают

= А .

Здесь Rⁿ и R^m − линейные пространства размерности n и m соответственно.

Если пространства Rⁿ и R^m совпадают, то оператор А отображает пространство Rⁿ в себя. Поэтому вместо Rⁿ можно писать просто R.

Оператор (преобразование) называется линейным, если для любых векторов и пространство R и любого числа выполняются соотношения:

А( + ) = А + А , А( ) = А (1)

Вектор = А называется образом вектора , а сам вектор прообразом вектора .

Линейный оператор (линейное преобразование) называется тождественным, если он преобразует любой вектор пространства R в самого себя:

Е = .

Нулевой оператор переводит все векторы пространства R в нулевые векторы: 0 = .

Пусть в линейном пространстве R , базис которого , ,…, , задан линейный оператор А. Так как А , А ,…, А − векторы пространства R, то каждый из них можно разложить единственным способом по векторам базиса:

А = а₁₁ +a₂₁ +…+ a_n1 ,

А = a₁₂ +a₂₂ +…+ a_n2 ,

. . . . . . . . . . . . . . . . . . . . . . . . . . (2)

А = a_1n +a_2n +…+ a_nn .

Матрица (3)

называется матрицей линейного оператора А в базисе , ,…, . Возьмем в пространстве R какой-нибудь вектор

= х₁ + х₂ +. . . + х_n .

Так как = А R, то и вектор А можно разложить по векторам базиса:

= А = у₁ + y₂ +. . . + y_n .

Координаты ( y_1, y₂,…, y_n ) вектора А выражаются через координаты ( х_1, х₂,…, х_n ) вектора по формулам:

(4)

Связь между векторами и = А в матричной форме:

Y = AX , (5)

где А – матрица линейного оператора, Х = (х_1, х₂,…, х_n)^т, Y = (y_1, y₂,…, y_n)^т.

Обобщая, можно сказать, что оператор А – это матрица А, с помощью которой каждому вектору = (х_1, х₂,…, х_n )  R ставится в соответствие вектор = (y_1, y₂,…, y_n)  R, компоненты которого вычисляются по формулам (4).

Пример. Оператор А в линейном пространстве R определен равенством А = + , где  R − фиксированный ненулевой вектор. Является ли оператор линейным?

□ Оператор А будет линейным, если выполняются условия (1). Следовательно, необходимо проверить выполнение этих условий. Согласно условию задачи

А = + , А = + , А( + ) = ( + ) + .

Согласно (1) А( + ) = А + А = ( + ) + ( + ). Значит, должно выполняться равенство

( + ) + = ( + ) + ( + ) или + + = + + 2 .

Равенство будет выполняться только при = , что противоречит условию задачи. Следовательно, оператор А не является линейным. ■

Пример. Дано линейное пространство геометрических векторов. Оператор А осуществляет замену каждого вектора его составляющей по оси Ох, т. е. А = . Является ли этот оператор линейным?

□ Пусть = + + и = + + – произвольные векторы, а λ – произвольное действительное число.

Для проверки условий (1) найдем сумму

+ =

и произведение λ = λ + λ + λ .

Тогда А( + ) = = + = А +А ,

А(λ ) = λ = λ А .

Следовательно, А − линейный оператор. ■

Действия над линейными операторами

Суммой двух линейных операторов А и В называется оператор

(А + В), определяемый равенством:

(А + В) = А + В .

Произведением линейного оператора А на число λ называется оператор λА, определяемый равенством:

(λА) = λ(А ).

Произведением линейных операторов А и В называется оператор АВ, определяемый равенством:

(АВ) = А( В ).

При сложении линейных операторов выполняется коммутативный закон; в общем случае АВ ≠ ВА..

Свойства операций:

А(ВС) = (АВ)С; АЕ = ЕА = А; (А+В)С = АС+ВС; С(А+В) = СА+СВ.

Если ВА = Е и АС = Е, то В = С.

В этом случае обозначают В = С = А⁻¹, линейный оператор А⁻¹ называют обратным линейным оператором по отношению к линейному оператору А, т. е. А⁻¹·А = А· А⁻¹ = Е.

Линейный оператор А в конечномерном пространстве называют невырожденным, если определитель матрицы этого оператора отличен от нуля. Каждый невырожденный оператор имеет только один обратный оператор.

Если невырожденный линейный оператор А в координатной форме определяется равенствами

(6)

то обратный оператор А⁻¹ имеет вид:

( 7 )

Здесь А_{i j} − алгебраическое дополнение элемента а_ij матрицы А, |А| − определитель матрицы А.

Матрица линейного оператора А⁻¹ является обратной по отношению к матрице А и определяется равенством

А⁻¹ = (8)

Теорема. Матрицы А и А^* линейного оператора А в базисах , ,…, и , ^*,…, ^* связаны соотношением

А^*= С⁻¹АС, (9)

где С − матрица перехода от старого базиса к новому.

Пример. Операторы (преобразования) А и В заданы равенствами

(A) и (B)

Найти операторы АВ и ВА.

□ Матрицы данных операторов имеют вид

А = , В = .

Найдем произведение этих матриц:

АВ = , ВА = .

В данном случае АВ = ВА, поэтому линейные операторы совпадают. Координатная форма оператора АВ записывается следующим образом:

■

Пример. Найти матрицу линейного оператора А⁻¹, если линейный оператор А имеет матрицу:

А = .

□ 1 способ. Матрица А определяет оператор =А , приводящий в соответствие каждому вектору = (х₁; х₂; х₃) вектор = (у₁; у₂; у₃) при помощи равенств:

Решая систему относительно х₁, х₂, х₃, получим

Эта система (равенства) определяет оператор =А⁻¹ , обратный к оператору А. Матрица этого оператора

А⁻¹ = .

2 способ. Элементы матрицы А⁻¹ можно получить путем вычислений по формуле (8). Имеем

,

, , ,

, , ,

, , .

Таким образом,

А⁻¹= . ■

Пример. В базисе , оператор (преобразование) А имеет матрицу А = . Найти матрицу оператора А в базисе ^*= +2 ; ^*= −2 + .

□ Здесь матрица перехода от старого базиса к новому имеет вид

С = . Обратная к ней матрица С⁻¹ = .

Следовательно, по формуле (9) имеем

А^*= С⁻¹АС = · · = . ■

Собственные векторы и собственные значения

линейного оператора

Вектор называется собственным вектором линейного оператора А, если найдется такое число , что

А = (10)

Число  называется собственным значением (характеристическим числом) оператора А (матрицы А ), соответствующим вектору .

Матричная запись равенства (10):

АХ = Х.

Если линейный оператор (линейное преобразование) А в базисе , ,…, имеет матрицу

,

то собственными числами линейного оператора А служат действительные корни ₁, ₂, …,_п уравнения n-й степени, которое имеет вид

.

Оно называется характеристическим уравнением, а его левая часть- характеристическим многочленом линейного оператора А (матрицы А). Собственным вектором , соответствующим собственному значению (характеристическому числу) _к, является любой вектор ₁ + ₂ +…+ + _n , координаты которого удовлетворяют системе линейных уравнений

Теорема. Характеристический многочлен линейного оператора не зависит от выбора базиса.

Теорема. Если матрица линейного оператора А является симметрической, то все корни характеристического уравнения – действительные числа.

Пример. Найти собственные значения и собственные векторы линейного оператора А, заданного матрицей А = .

□ Составим характеристическое уравнение или .

Тогда собственные значения линейного оператора А: λ₁= −5, λ₂ = 7.

Для каждого значения составим систему линейных уравнений и найдем координаты собственного вектора.

Пусть λ = −5, тогда или

или .

Таким образом, значения ξ₁ и ξ₂ должны удовлетворять уравнению , или ξ₂ = −1,5ξ₁. Следовательно, решение этой системы имеет вид: ξ₁ = С₁, ξ₂ = −1,5С₁, где С₁ − произвольное число, . Поэтому собственному значению λ = −5 соответствует семейство собственных векторов , т.е.

.

Значение λ = 7 приводит к системе

или

Значит, значения и должны удовлетворять уравнению , или ξ₂ = 1,5ξ₁. Следовательно, ξ₁ = С₂, ξ₂ = 1,5С₂ , где С₂ − произвольная величина, . Собственному значению λ = 7 соответствует семейство собственных векторов

.

Итак, придавая в равенствах , величинам С₁ и С₂ всевозможные числовые значения, будем получать всевозможные собственные векторы оператора А. ■

Пример. Найти характеристические числа и собственные векторы линейного оператора А, определяемого уравнениями

□ Матрица оператора запишется так: А = .

Характеристическое уравнение: или

;

характеристические числа (собственные значения): λ₁ = 1, λ₂ = 13.

Для λ = 1 система уравнений имеет вид

или

Значит, значения и должны удовлетворять уравнению , или ξ₂ = − ξ₁. Следовательно, ξ₁ = С₁, ξ₂ = − С₁. Поэтому собственному значению λ = 1 соответствует семейство собственных векторов .

Для λ = 13 система уравнений имеет вид

или

Значит, значения и должны удовлетворять уравнению , или ξ₂ = 2ξ₁. Следовательно, ξ₁ = С₂, ξ₂ = 2С₂. Поэтому собственному значению λ = 13 соответствует семейство собственных векторов .

Придавая в равенствах , величинам С₁ и С₂ всевозможные ненулевые числовые значения, будем получать всевозможные собственные векторы линейного оператора А. ■