§ 12. Скалярное произведение векторов

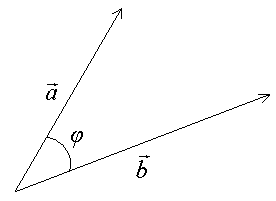
Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

= ∙ = ( , ) = | |∙| | . (1)

Очевидно:

∙ = | | = | | .

Свойства скалярного произведения:

1⁰. ∙ = = | |² − скалярный квадрат;

2⁰. ∙ = 0, если = , либо = , либо ;

3⁰. ∙ = ∙ (коммутативный закон);

4⁰. ∙( + ) = ∙ + ∙ (дистрибутивный закон);

5⁰. (т )∙ = ∙(т ) = т( ∙ ) (ассоциативный закон по отношению к скалярному множителю).

Механический смысл скалярного произведения:

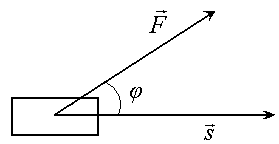
Если тело под действием силы передвинулось прямолинейно вдоль вектора , то работа А, выполненная силой равна

А = | |∙| | .

Скалярное произведение ортов осей координат:

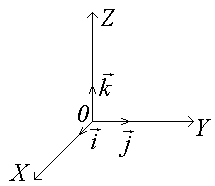
∙ = ∙ = ∙ = 1, ∙ = ∙ = ∙ = 0. (2)

Пусть заданы векторы = а_х + а_у + a_z и = b_х + b_y + b_z . Найдем их скалярное произведение:

∙ = (а_х + а_у + a_z )∙( b_х + b_y + b_z ) = а_хb_х( ∙ ) + а_хb_у( ∙ ) +

+ а_хb_z( ∙ ) + а_yb_х( ∙ ) + а_yb_y( ∙ ) + а_yb_z( ∙ ) + а_zb_х( ∙ ) +

+ а_zb_y( ∙ ) + а_zb_z( ∙ ) = а_хb_х + а_yb_y + а_zb_z .

Таким образом, если известны координаты векторов и , то

∙ = а_хb_х + а_yb_y + а_zb_z . (3)

Из формул (1) и (3) вытекает формула нахождения угла между векторами:

= = . (4)

Ненулевые векторы и называются ортогональными, если

∙ = 0.

Отсюда следует признак ортогональности :

для того, чтобы ненулевые векторы и были ортогональны, необходимо и достаточно, чтобы угол между ними был равен φ = .

Пример. Найти скалярное произведение (5 + 3 )∙(2 − ), если | | = 2, | | = 3, .

□ Используя свойства скалярного произведения и данные условия, получим:

(5 +3 )∙(2 − ) = 5 ∙2 −5 ∙ + 3 ∙2 − 3 ∙ = 10 − 5( ∙ ) +

+ 6( ∙ ) − 3 = 10 − 3 = 10∙2² − 3∙3² = 40 − 27 = 13. ■

§ 13. Векторное произведение векторов

Векторным произведением вектора на вектор называется третий вектор = × = [ , ], который:

1. имеет модуль, численно равный площади параллелограмма, построенного на векторах и ( | | = | |∙| | , где φ − угол между векторами и );

2. перпендикулярен векторам и ;

3. направлен в ту сторону, из которой кратчайшее вращение от к происходит против часовой стрелки.

Свойства векторного произведения:

1⁰. × = − × ;

2⁰. × = , если = , либо = , либо || ;

3⁰. (т ) × = × (т ) = т( × ) (ассоциативный закон по отношению к скалярному множителю);

4⁰. × ( + ) = × + × (дистрибутивный закон).

Механический смысл векторного произведения:

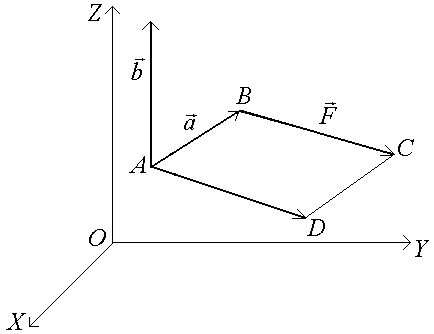
Пусть заданы две точки А и В. Пусть к точке В приложена сила . Пусть = . Моментом силы относительно точки А есть векторное произведение вектора на вектор :

= × .

Векторное произведение ортов осей координат:

× = × = × = , (1)

× = − × = , × = − × = , × = − × = . (2)

Вообще произведение любых векторов в последовательности

дает следующий вектор со знаком (+), а в обратной последовательности − со знаком (−).

Если известны координаты векторов и :

= (а_х, а_у, a_z) = а_х + а_у + a_z и = (b_х, b_y, b_z) = b_х + b_y + b_z ,

то векторное произведение векторов и можно вычислить по формуле

× = . (3)

Площадь параллелограмма, построенного на векторах и :

S = | × |. (4)

Площадь треугольника, построенного на векторах и :

S_Δ = | × |. (5)

Признак коллинеарности

Для того, чтобы ненулевые векторы и были коллинеарны, необходимо и достаточно, чтобы × = .

В этом случае из (3) следует, что координаты векторов и пропорциональны, т.е.

= = .

Пример. Вычислить площадь параллелограмма, построенного на векторах + 3 и 3 + , если | | = | | = 1, угол между векторами φ = 30⁰.

□ Так как площадь параллелограмма равна модулю векторного произведения данных векторов, то найдем это векторное произведение, учитывая свойства векторного произведения:

( + 3 ) × (3 + ) = 3 × + × + 9 × + 3 × = 3∙ + × −

−9 × + 3∙ = −8 × .

Тогда

S = |−8 × | = 8| × | = 8∙| |∙| | = 8∙1∙1∙ = 4(кв. ед.). ■