Глава 3. Аналитическая геометрия на плоскости

§ 1. Уравнение линии

Уравнение линии в прямоугольной системе координат

Уравнением линии (кривой) на плоскости ОХY называется уравнение

F(x, y) = 0,

которому удовлетворяют координаты х и у каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

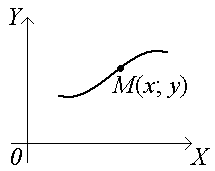
Если точка М(х; у) передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты х и у точки М(х; у) называют текущими координатами.

Пример. Составить уравнение геометрического места точек, одинаково удаленных от начала координат и от точки А(−5; 3).

□ Пусть точка М(х; у) является произвольной точкой геометрического места точек. Из условия задачи следует, что АМ = ОМ:

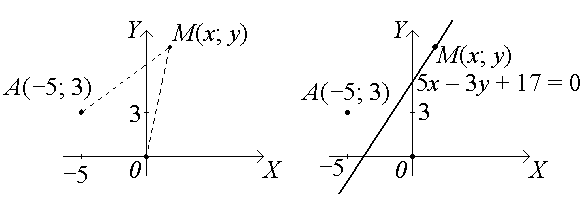
Учитывая, что расстояние d между точками М₁(х₁; у₁) и М₂(х₂; у₂) определяется по формуле

d = ,

получим

АМ = ,

ОМ = .

Тогда,

= .

Сделаем преобразования:

(х + 5)² + (у − 3)² = х² + у²,

х² + 10х + 25 + у² − 6у + 9 = х² + у²,

10х − 6у +34 = 0.

Окончательно, получим уравнение геометрического места точек (уравнение линии):

5х − 3у +17 = 0.

Линией является прямая. ■

Уравнение линии в полярной системе координат

Говорят, что на плоскости заданна полярная система координат, если заданы: некоторая точка О, называемая полюсом; некоторый луч L, исходящий из точки О, называемый полярной осью.

Полярными координатами точки М, не совпадающей с полюсом О, являются два числа: полярный радиус ρ = | | > 0 и полярный угол φ – угол между полярной осью и вектором . При этом φ > 0, если угол отсчитывается против часовой стрелки, и φ < 0 в противном случае

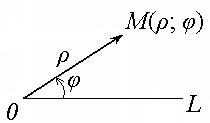
Если совместить полюс О с началом координат OXY, а полярную ось с положительной полуосью абсцисс, то координаты (х; у) точки М и ее полярные координаты (ρ; φ) будут связаны зависимостями:

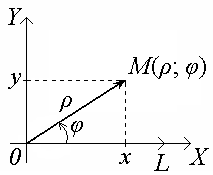
Уравнение линии в полярной системе координат можно получить либо непосредственно из геометрических свойств кривой, либо переводом уравнения этой линии, заданного в декартовой системе координат.

Пример. Записать уравнение линии у = х в полярных координатах.

□ Подставим в заданное уравнение уравнения перехода

х = ρcosφ, y = ρsinφ.

В результате получим

ρsinφ = ρcosφ или tgφ = 1.

Окончательно, φ = − искомое уравнение линии. ■

Параметрические уравнения линии

Пусть х и у координаты некоторой точки М. Рассмотрим две функции аргумента t: х = φ(t), y = ψ(t).

При изменении t величины х и у будут также меняться, следовательно, точка М будет перемещаться. Написанные равенства называются параметрическими уравнениями линии, которая является траекторией точки М; аргумент t называют параметром.

Если из равенств можно исключить параметр t, то получим уравнение траектории точки М в виде F(x; y)= 0.

Пример. Составить параметрические уравнения окружности с центром в начале координат.

□ Рассмотрим окружность радиуса r с центром в начале координат.

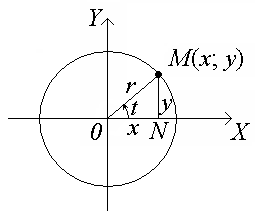
Возьмем на ней произвольную точку М(х; у) . Примем за параметр t угол, образованный с осью абсцисс радиусом ОМ = r. Из треугольника OMN следует, что

х = rcost, y = rsint.

Эти уравнения и являются параметрическими уравнениями окружности.

Исключив из этих уравнений параметр t, получим уравнение окружности в прямоугольной системе координат OXY. Для этого возведем каждое уравнение в квадрат и полученные уравнения сложим:

х² + у² = r²cos²t + r²sin²t = r²(cos²t + sin²t),

т.е.

х² + у² = r².

Это уравнение является уравнением окружности радиуса r с центром в начале координат. ■