§ 5. Классификация кривых второго порядка
Пусть задано общее уравнение кривой второго порядка
Ах2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0. (1)
Если:
1. АС − В2 > 0, то уравнение (1) представляет собой эллипс, точку
(х2 + у2 = 0) или мнимую кривую. В этом случае говорят, что кривая принадлежит к эллиптическому типу;
2. АС − В2 < 0, то уравнение (1) представляет собой гиперболу или пару пересекающихся прямых (а2х2 − b2у2 = 0, а,b > 0). В этом случае говорят, что кривая принадлежит к гиперболическому типу;
3. АС − В2 = 0, то уравнение (1) представляет собой параболу, пару параллельных или совпадающих прямых (х2 − а2 = 0, а ≥ 0) или мнимую кривую. В этом случае говорят, что кривая принадлежит к параболическому типу.
Пример. К какому типу относится кривая второго порядка
17x2 + 12xy + 8у2 − 80 = 0.
□ Имеем А
= 17,
= 6, С
= 8. Тогда
АС − В2 = 17· 8 − 62 = 136 − 36 = 100 > 0.
Следовательно, заданная кривая относится к эллиптическому типу. ■
§ 6. Приведение общего уравнения кривой второго порядка к каноническому виду
При совершении этой операции необходимо знать формулы преобразования координат.
Параллельный перенос:
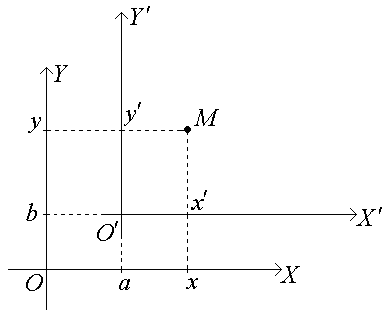
При
переходе от системы координат OXY
к новой системе координат
связь между старыми и новыми координатами
некоторой точки М
плоскости определяется формулами:
х
=
+ а,
у
=
+ b,
(1)
= х − а, = у − b. (2)
Новое
начало координат:
= (а;
b).
Поворот осей координат:
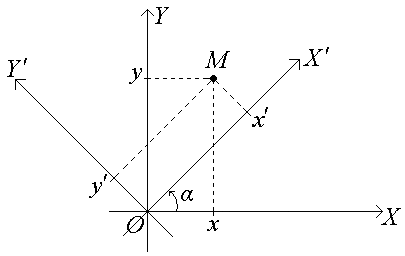
Угол
α отсчитывается
против часовой стрелки. Связь между
старыми координатами х,
у
и новыми координатами
,
некоторой точки М
определяется по формулам:
х = − , у = + , (3)
=
х
+ у
,
=
−х
+ у
.
(4)
Поворот осей координат позволяет удалить из уравнения кривой второго порядка член с произведением координат, т.е. произведение ху.
Пример. Привести к каноническому виду уравнение
х2 − 2ху + у2 −10x −6y + 25 = 0.
□ Здесь А = 1, В = −1, С = 1. Тогда
АС − В2 = 1∙1 − (−1)2 = 0.
Значит, кривая является параболического типа.
Исключим из уравнения произведение ху. Для этого преобразуем уравнение с помощью формул поворота осей:
(
−
)2
−
2(
−
)∙(
+
)
+
+ ( + )2 − 10( − ) − 6( + ) +
+ 25 = 0
или
(
−2
+
)
+
(
+
2
+
)
+
+
2(
−
)
−
(10
+6
)
+
(10
−
6
)
+
+ 25= 0.
Приравнивая нулю коэффициент при , получим
2( − ) = 0.
Откуда
= 1, т.е.
или
.
Возьмем
,
отсюда α
=
и
=
,
=
.
Тогда, уравнение примет вид
2
− 8
+ 2
+ 25 = 0
или
2( + ) − 8 + 25 = 0.
Дополним выражение в скобках до полного квадрата:
2(
+
)2
= 8
− 24
или
(
+
)2
= 4
(
−
).
Совершим параллельный перенос:
новое начало координат ( ; − ), новые координаты
=
−
,
=
+
.
Тогда, получим
= 4
.
Таким
образом, получили уравнение параболы.
Схематичное расположение параболы
относительно координат
,
и OXY:
■
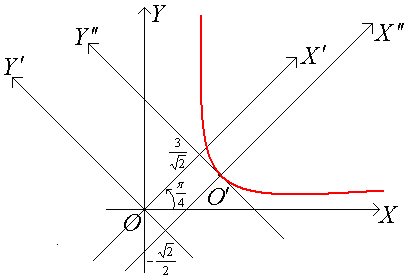
Замечание. Если в выражении кривой второго порядка отсутствует произведение ху, то при приведении уравнения к каноническому виду сразу используется параллельный перенос координат.
Пример. Привести к каноническому виду уравнение
9x2 – 6x – y + 2 = 0.
□ Здесь A = 9, B = 0, C = 0. Тогда AC – B2 = 9·0 – 02 = 0, т.е. кривая параболического типа.
Так как в заданном уравнении не присутствует член xy, то поворот осей совершать не надо.
Выделим полный квадрат в заданном уравнении:
9x2
– 6x – y + 2 = 0, (9x2
–
x)
– y + 2 = 0,
9((x2
–
x
+
)
–
)
– y + 2 = 0,
9(x – )2 – 1 – y + 2 = 0
или
9(x – )2 = y – 1.
В результате получим (x – )2 = (y – 1).
Совершим
параллельный перенос: новое начало
координат
(
;
1),
,
.
Тогда
,
т.е. получили параболу. ■
Иногда для упрощения уравнения кривой можно воспользоваться другими методами.
Пример. Какая линия определяется уравнением
9x2 + 24xy + 16y2 – 25 = 0 ?
□ Здесь A = 9, B = 12, C = 16. Тогда AC – B2 = 9·16 – 122 = 0, т.е. кривая параболического вида.
Если идти по традиционному пути, то мы должны сначала совершить поворот осей, а потом параллельный перенос.
Но можно упростить решение. Заметим, что первые три члена образуют полный квадрат двух чисел:
9x2 + 24xy + 16y2 – 25 = 0,
т.е.
(3x + 4y)2 – 25 = 0.
Теперь слева от равенства стоит разность квадратов:
(3x + 4y + 5)(3x + 4y – 5) = 0.
Полученная запись означает, что заданное уравнение определяет пару параллельных прямых 3x + 4y + 5 = 0 и 3x + 4y – 5 = 0. ■
Пример. Какая линия определяется уравнением
xy + 2x – 4y – 8 = 0 ?
□ Здесь
A = 0, B
=
,
C = 0. Тогда AC
– B2
= 0·0 – (
)2
=
<
0, т.е. кривая гиперболического типа.
Преобразуем заданное уравнение:
xy + 2x – 4y – 8 = 0, x(y + 2) – 4(y + 2) = 0.
Окончательно (x – 4)(y + 2) = 0. Таким образом, заданное уравнение определяет пару пересекающихся прямых x – 4 = 0 и y + 2 = 0 причем одна из них параллельна оси OX, а другая параллельная оси OY. ■
Для приведения к каноническому виду общего уравнения кривой второго порядка можно использовать линейное ортогональное преобразование. Для этого следует:
а) найти линейное ортогональное преобразование, которое приводит квадратичную форму старших членов уравнения кривой к сумме квадратов, и выполнить в уравнении соответствующую замену. В результате из уравнения исчезают члены с произведениями координат;
б) произведя после этого параллельный перенос новых осей координат, приводят уравнение к требуемому виду.
Пример. Привести к каноническому виду уравнение линии
17x2 + 12xy + 8у2 − 80 = 0.
□ Группа старших членов уравнения образует квадратичную форму
f(x,y) = 17x2 + 12xy + 8у2 с матрицей
.
Составим характеристическое уравнение
или
,
т.
е.
Следовательно, квадратичная форма f(x,y) преобразуется к каноническому виду
f
(
,
)
= 5
2
+ 20
2
а данное уравнение – к виду
5 2 + 20 2 − 80 = 0 или
или
т.е. заданная кривая является эллипсом.
Найдем базис, в котором уравнение эллипса принимает канонический вид. Для этого определим собственные векторы.
При
имеем систему уравнений
откуда,
Полагая
,
получим
,
т.е. собственный вектор
При
имеем систему уравнений
откуда,
,
т.е. собственный вектор
Нормируя векторы, получим
,
.
Матрица ортогонального преобразования имеет вид
В =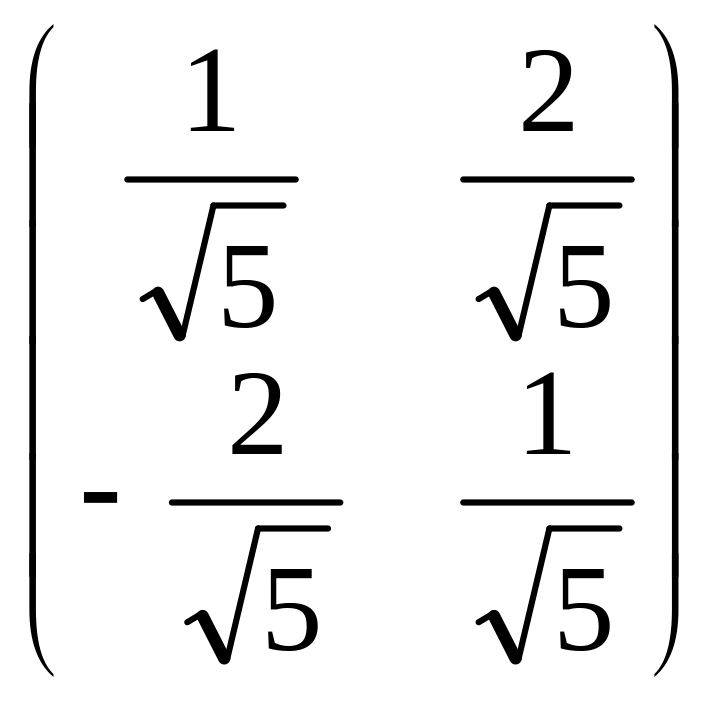
.
Формулы преобразования координат:
Следовательно,
.
■
Пример. Привести к каноническому виду уравнение кривой
9x2 + 24xy + 16y2 − 230x + 110y − 225 = 0.
□ В данном случае f(x,y) = 9x2 + 24xy + 16y2 с матрицей
А =
.
Составим характеристическое уравнение
, или
,
т.е.
.
Для
получим систему
откуда
.
Полагая
получаем
,т.
е. собственный вектор
Для
получаем систему
откуда
.
Полагая
получаем
,т.
е. собственный вектор
Нормируя векторы, получим
,
.
Матрица
ортогонального преобразования: В
=
.
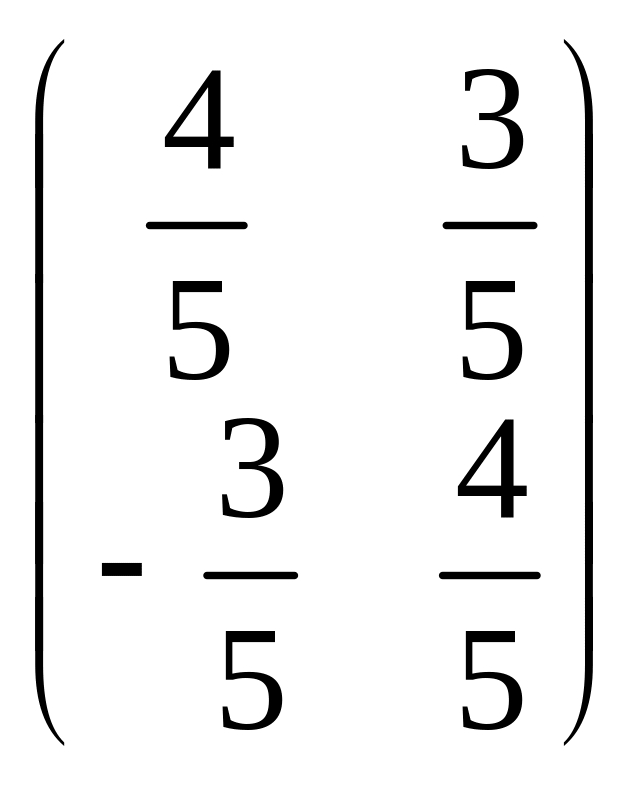Формулы
преобразования координат:
Следовательно, учитывая, что ,
,
т. е.
2 − 10 − 2 − 9 = 0.
Последнее уравнение можно переписать в виде
(
−
1)2 =
10(
+
1 ).
Произведя
параллельный перенос осей, примем за
новое начало координат точку
(−1;1).
В итоге приходим к каноническому
уравнению заданной кривой
,
которая является параболой. ■