Глава 4. Аналитическая геометрия в пространстве

§ 1. Уравнение поверхности

Уравнение

F(x, y, z) = 0

называется уравнением поверхности, которому удовлетворяют координаты каждой точки, лежащей на этой поверхности, и не удовлетворяют координаты никакой точки, не лежащей на ней.

Если точка М(х, у, z) передвигается по поверхности, то ее координаты, изменяясь, удовлетворяют уравнению этой поверхности. Поэтому координаты точки М(х, у, z) называются текущими координатами.

Пример. Установить, какие геометрические образы определяются следующими уравнениями в декартовых прямоугольных координатах пространства:

а) у − 2 = 0; б) ху = 0.

□ Отметим, что в уравнение поверхности входят три переменные: х, у и z.

а) В уравнении поверхности у − 2 = 0 отсутствуют переменные х и z. Это означает, что они могут принимать любые значения (т.к. коэффициенты при этих переменных равны нулю). Так как ордината

у = 2, то заданное уравнение описывает плоскость, параллельную плоскости OXZ и пересекающую ось ОY в точке с ординатой у = 2.

б) В уравнении ху = 0 отсутствует переменная z. Значит, она принимает любые значения. Заданное уравнение имеет два решения: либо х = 0, либо у = 0. Вывод: заданное уравнение описывает две плоскости: OYZ (при х = 0) и OXZ (при у = 0). ■

§ 2. Плоскость

1). Ах + Ву + Сz + D = 0. (1)

Здесь А ≠ 0, В ≠ 0, С ≠ 0 (одновременно).

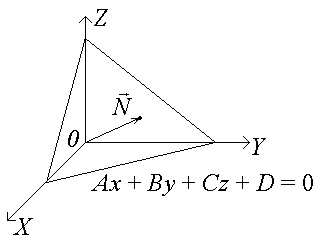
(1) − общее уравнение плоскости.

Коэффициенты А, В и С можно рассматривать как координаты вектора = (А; В; С), перпендикулярного к плоскости. Вектор

= (А; В; С) − нормальный вектор плоскости.

Частные случаи:

1. Если D = 0, то (1) проходит через начало координат;

2. Если С = 0, то (1) представляет собой плоскость, параллельную оси OZ (или, что то же самое, перпендикулярную плоскости OXY);

3. Если С = 0, D = 0, то (1) проходит по оси OZ;

4. Если С = 0, В = 0, то (1) перпендикулярна оси ОХ ( или параллельна плоскости OYZ) и т.д.

Уравнения, вытекающие из уравнения (1), аналогичны уравнениям, вытекающим из общего уравнения прямой Ах + Ву + С = 0 (добавляется аппликата z).

2). А(х − х₀) + В(у − у₀) + С(z − z₀) = 0. (2)

(2) − уравнение плоскости, проходящей через заданную точку М₀(х₀; у₀; z₀) перпендикулярно вектору = (А; В; С).

3). Угол между плоскостями

Пусть заданы две плоскости

А₁х + В₁у + С₁z + D₁ = 0, = (А₁; В₁; С₁),

А₂х + В₂у + С₂z + D₂ = 0, = (А₂; В₂; С₂).

Тогда

cosφ = = . (3)

Условие перпендикулярности плоскостей:

А₁А₂ + В₁В₂ + С₁С₂= 0. (4)

Условие параллельности плоскостей:

= = . (5)

4). Уравнение плоскости в отрезках:

+ + = 1. (6)

5). Пусть вектор является нормальным вектором плоскости. Пусть | |= р.

Уравнение

∙ = р, (7)

где = (х; у; z) − радиус-вектор текущей точки плоскости; = (cosα; cosβ; cosγ) − единичный вектор, направленный в ту же сторону, что и , является векторным уравнением плоскости, а уравнение

х cosα + y cosβ + zcosγ = р (8)

является нормальным уравнением плоскости.

Если плоскость задана общим уравнением (1), то его можно привести к нормальному виду, умножив на нормирующий множитель

М = ,

где знак множителя берется противоположным знаку D в уравнении (1).

6). Расстояние от точки М₀(х₀; у₀; z₀) до плоскости Ах + Ву + Сz + D = 0:

. (9)

7) Пусть заданы три точки М₁(х₁;у₁;z₁), М₂(х₂; у₂; z₂) и М₃(х₃; у₃; z₃), не лежащие на одной прямой. Требуется написать уравнение плоскости, проходящей через эти точки. Так как плоскость проходит через каждую точку, то должны выполняться условия

где А, В, С одновременно не равны нулю. Получили однородную линейную систему уравнений, которой удовлетворяет нетривиальный вектор = (А; В; С). Следовательно, определитель этой системы должен равняться нулю

= 0. (10)

(10) − уравнение плоскости, проходящей через три заданные точки М₁(х₁; у₁; z₁), М₂(х₂; у₂; z₂) и М₃(х₃; у₃; z₃).

Пример. Написать уравнение плоскости, проходящей через точку М(2;−1; 4) параллельно двум векторам = (1; 3; −5) и = (1; 1; 2).

□ Воспользуемся уравнением плоскости, проходящей через заданную точку М₀(х₀; у₀; z₀) перпендикулярно нормальному вектору

= (А; В; С):

А(х − х₀) + В(у − у₀) + С(z − z₀) = 0.

Имеем х₀ = 2, у₀ = −1, z₀ = 4. Так как искомая плоскость параллельна векторам и , то ее нормальный вектор должен быть перпендикулярен этим векторам. Такому условию удовлетворяет векторное произведение этих векторов. Его и примем за = (А;В;С). Итак

= × = = 11 −7 −2 = (11; −7; −2).

Запишем уравнение плоскости

11(х − 2) − 7(у + 1) −2(z − 4) = 0

или

11х − 7у −2z − 21 = 0. ■