§ 17. Квадратические формы

Квадратичной формой действительных переменных называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени.

Если − квадратичная форма, а λ – какое-нибудь действительное число, то

= λ .

Если n = 2, то

.

Если n = 3, то

Далее будем рассматривать квадратичную форму трех переменных.

Матрица

,

у которой , называется матрицей квадратичной формы , а соответствующий определитель − определителем этой квадратичной формы.

Так как А − симметрическая матрица, то корни характеристического уравнения

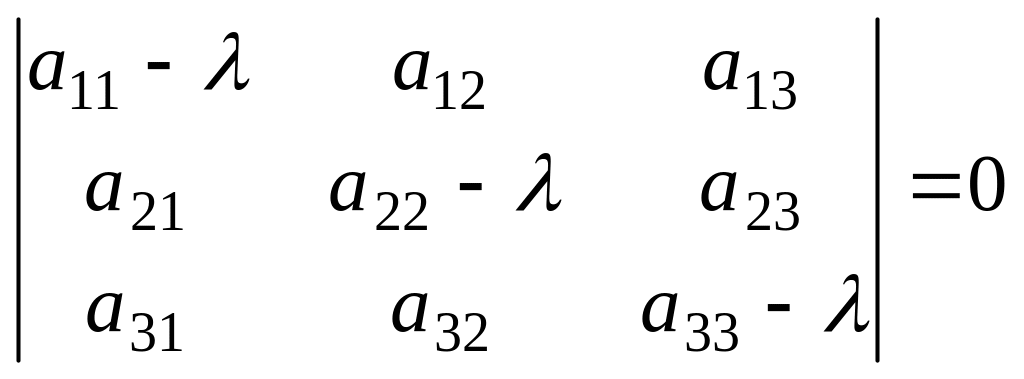
являются действительными числами.

Пусть

нормированные собственные векторы, соответствующие характеристическим числам в ортонормированном базисе . В свою очередь, векторы образуют ортонормированный базис. Матрица

В =

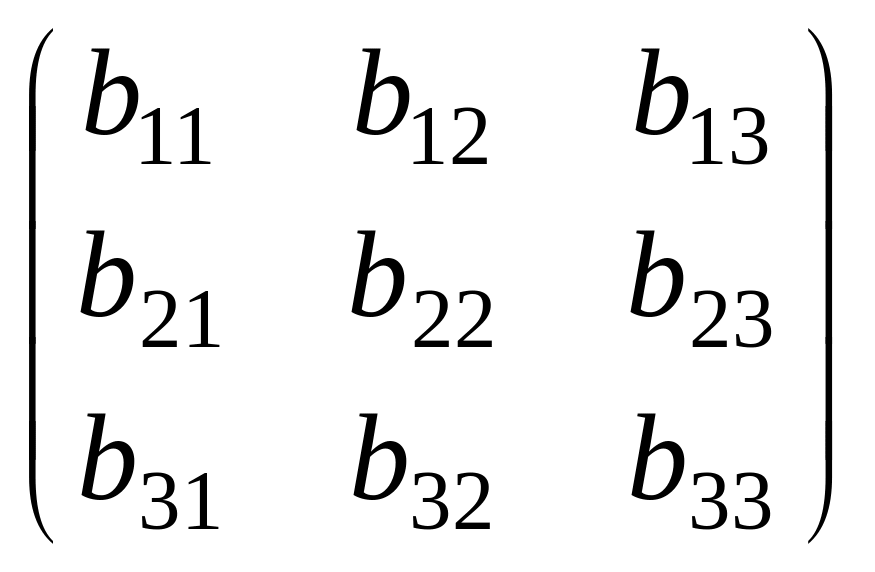
является матрицей перехода от базиса к базису .

Формулы преобразования координат при переходе к новому ортонормированному базису имеют вид

Преобразовав с помощью этих формул квадратичную форму , получаем квадратичную форму

= λ₁ ²+ λ₂ ²+ λ₃ ²

которая не содержит членов с произведениями , , .

Принято говорить, что квадратичная форма приведена к каноническому виду с помощью ортогонального преобразования в.

Пример. Привести к каноническому виду квадратичную форму

.

□ Имеем , , .

Составим характеристическое уравнение:

или .

Решая уравнение, найдем характеристические числа (собственные значения)

Определяем собственные векторы. Если то получаем систему уравнений

Отсюда получим . Полагая , имеем т.е. собственный вектор

Нормируем этот вектор

Если , то получаем систему

В этом случае получаем собственный вектор

.

Нормируя этот вектор, имеем

Итак, найденные нормированные собственные векторы:

Матрица перехода от ортонормированного базиса к ортонормированному базису имеет вид

В = .

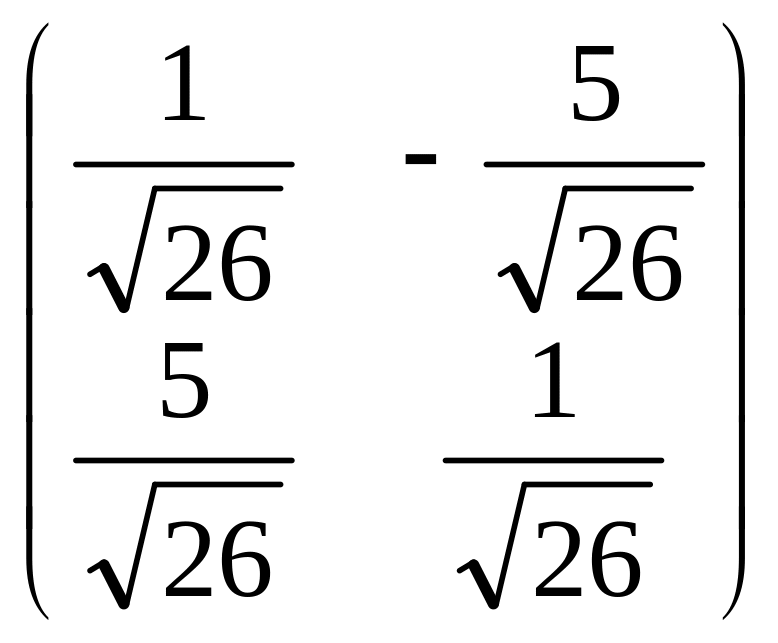Отсюда получаем формулы преобразования координат:

Таким образом,

.

Раскрывая скобки, получим

.

Этот результат можно было получить сразу, так как

. ■

Пример . Привести к каноническому виду квадратичную форму

□ Здесь , , , , , . Решив характеристическое уравнение:

,

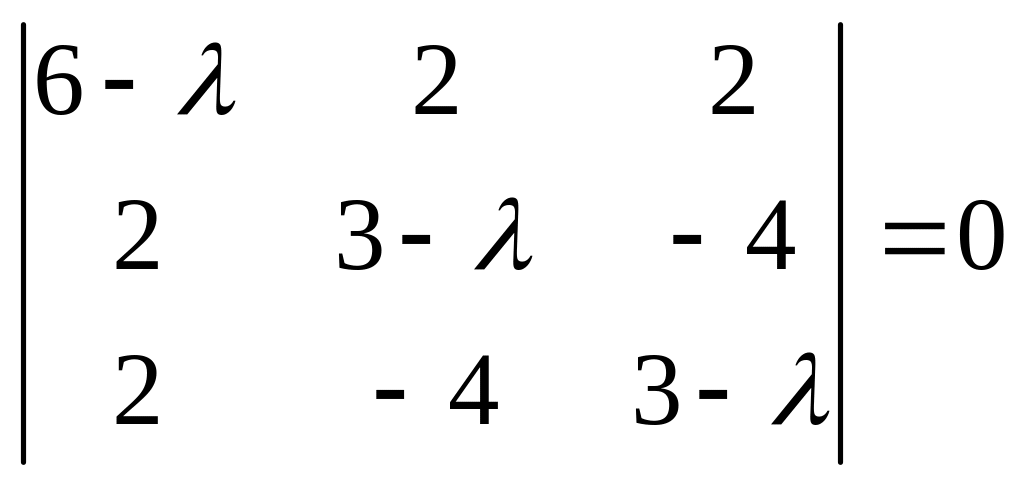получим ; .

При приходим к системе

которая сводится к одному уравнению .

Решение этой системы можно записать в виде , , . В результате получаем семейство собственных векторов

,

зависящее от двух параметров .

При получаем систему

Решив систему, получим , . Таким образом, получим однопараметрическое семейство собственных векторов

Из семейства собственных векторов выделим два каких-нибудь ортогональных вектора. Полагая, например, ,

b = 1, получим собственный вектор

.

Подберем параметры и b так, чтобы выполнялось равенство

.

Тогда получим уравнения

т.е. .

Теперь можно принять , b = − 4; отсюда находим другой собственный вектор рассмотренного семейства:

.

Таким образом, мы получили три попарно ортогональных вектора:

, ,

Собственные векторы , соответствуют характеристическому числу , а собственный вектор − характеристическому числу при С = 1.

Пронормировав эти векторы, получим

, ,

.

Получили новый ортонормированный базис, причем матрица перехода к новому базису имеет вид

В = .

Применив формулы преобразования координат:

к заданной квадратичной форме, получим

. ■