§ 3. Прямая в пространстве
1). Прямую в пространстве можно задать, как линию пересечения двух плоскостей
(1)
где А1, В1, С1 и А2, В2, С2 не пропорциональны.
2).
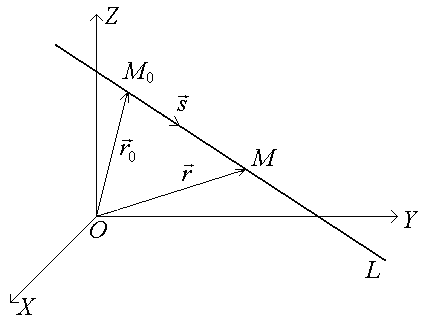
Рассмотрим
в пространстве произвольную прямую L,
проходящую через точку М0(х0;
у0;
z0).
Пусть
= (х0;
у0;
z0)
− радиус-вектор точки М0;
= (т;
п;
р)
− направляющий вектор; М(х;
у;
z)
− текущая точка прямой;
= (х;
у;
z)
− радиус-вектор точки М.
Тогда можно записать
− = t ,
где t − скаляр (число).
Если действительная переменная t пробегает интервал (−∞, +∞), то конец вектора = + t пробегает всю прямую L.
Поэтому, уравнение
− = t , (−∞ < t < +∞) (2)
называют векторным уравнением прямой, проходящей через точку М0(х0; у0; z0). и направленной в сторону вектора = (т; п; р).
3). Запишем (2) в координатной форме
или
(3)
(3) − параметрические уравнения прямой, проходящей через точку М0(х0; у0; z0) ( t − параметр).
4). Исключая из (3) параметр t, получим
=
=
.
(4)
(4) − канонические уравнения прямой, проходящей через точку М0(х0; у0; z0) параллельно направляющему вектору = (т; п; р).
5). Угол между прямыми.
Пусть даны две прямые
=
=
,
=
=
.
Угол
между этими прямыми равен углу между
их направляющими векторами
= (т1;
п1;
р1)
и
=
(т2;
п2;
р2):
=
.
(5)
Условие перпендикулярности прямых:
В этом случае ∙ = 0. Значит,
т1т2 + п1п2 + р1р2= 0. (6)
Условие параллельности прямых:
В этом случае векторы и коллинеарны. Значит,
=
=
.
(7)
6). Уравнения прямой, проходящей через две заданные точки М1(х1; у1; z1) и М2(х2; у2; z2):
=
=
.
(8)
Пример. Записать канонические уравнения прямой
□ Для записи канонических уравнений прямой
= =
необходимо найти координаты направляющего вектора = (т; п; р) и координаты точки М0(х0; у0; z0), лежащей на этой прямой.
За направляющий вектор можно принять векторное произведение нормальных векторов заданных плоскостей: = (1; 2; 3) и = (3; 1; 4). Тогда
=
×
=
=5
+5
−5
= (5; 5; −5).
Координаты точки М0 на прямой найдем, задав z = 0 и решив систему уравнений относительно х и у:
Имеем М0(3; 5; 0).
Подставив полученные данные в канонические уравнения прямой, получим
=
=
или
=
=
.
■