§ 9. Двумерные векторы (векторы на плоскости)

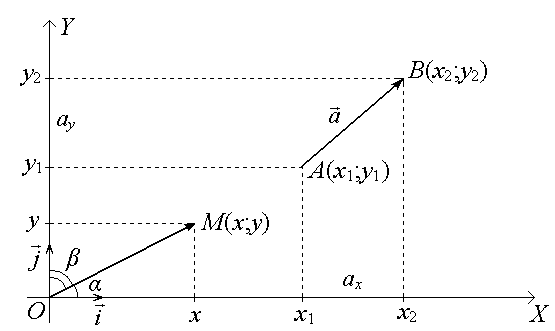
Пусть дана координатная плоскость.

Вектор , начало которого находится в начале координат, а конец в точке М(х; у), называется радиус-вектором точки М и обозначают = .

Радиус-вектор можно записать в виде

= (х; у), (1)

где х, у – проекции вектора на оси координат ОХ и ОY соответственно или прямоугольные координаты радиус-вектора (координаты или компоненты ).

Модуль (длина) :

| | = . (2)

Единичные векторы координатных осей и называются ортами.

Запись радиус-вектора через орты:

= х + у , (3)

где х , у − составляющие вектора по осям координат.

Произвольный вектор , заданный в координатной плоскости OXY, может быть записан в виде

= (а_х; а_у), (4)

где а_х, а_у – проекции вектора на соответствующие оси координат (координаты или компоненты вектора).

Запись (1) или (4) называют записью вектора в координатной форме.

Длина (модуль) вектора :

| | = . (5)

Запись вектора через орты:

= а_х + а_у , (6)

где а_х , а_у − составляющие вектора по осям координат.

Запись (3) или (6) называют разложением вектора по осям координат или разложением по ортам.

Вектор , имеющий начало в точке А(х₁; у₁) и конец в точке В(х₂; у₂), записывается в координатной форме и в разложении по ортам следующим образом:

= (х₂ − х₁; у₂ − у₁) = (х₂ − х₁) + (у₂ − у₁) . (7)

Длина вектора :

| | = . (8)

Направление вектора определяется углами α и β, образованными вектором с осями координат ОХ и ОY соответственно.

Косинусы этих углов называются направляющими косинусами вектора и определяются по формулам:

, . (9)

Свойство направляющих косинусов:

+ = 1.

Если векторы и заданы в координатной форме или в виде разложения по ортам (известны координаты векторов), то

± = (а_х ± b_х; а_y ± b_y) = (а_х ± b_х) + (а_y ± b_y) . (10)

Произведение вектора на скалярный множитель т:

т = (та_х; та_у) = та_х + та_у . (11)

Если т = , то вектор имеет длину, равную единице, и направление, совпадающее с направлением вектора . Этот вектор называют единичным вектором (ортом) вектора и обозначают через ₀.

Нахождение единичного вектора того же направления, что и данный вектор , называется нормированием вектора .

Таким образом,

₀ = . (12)

Очевидно, что координатные орты и имеют следующие координаты :

= (1; 0), = (0; 1).

Пример. На плоскости даны точки А(1; 3) и В(5; 8). Найти:

1) вектор = ; 2) длину вектора ; 3) направляющие косинусы вектора ; 4) нормировать вектор ; 5) вектор = 3 ; 6) вектор

= − .

□ 1) По формуле (7) имеем:

= = (х₂− х₁; у₂− у₁) = (5− 1; 8− 3) = (4; 5) − в координатной форме;

= 4 + 5 − в виде разложения по ортам;

2) по формуле (5) имеем:

| | = = = = ;

3) по формулам (9) имеем:

= , = .

Зная направляющие косинусы, всегда можно найти углы α и β, образованные вектором с осями координат ОХ и ОY , т.е. определить направление вектора ;

4) по формуле (12) имеем:

₀ = = = + ,

В координатной форме:

₀ = ;

5) по формуле (11) имеем:

= 3 = 3(4 + 5 ) = 12 + 15 ;

6) по формуле (10) имеем:

= − = (b_х − a_х; b_y − a_y) = (12 − 4; 15 − 5) = (8; 10) = 8 + 10 . ■