§ 16. Евклидово пространство
Линейное
пространство R
называется евклидовым,
если имеется правило, которое позволяет
для каждых двух векторов
и
из R
построить действительное число,
называемое скалярным произведением
векторов
и
и обозначаемое (
,
),
причем это правило удовлетворяет
условиям:
10
(
,
)
= (
,
);
20
(
,
+
)
= (
,
)
+ (
,
);
30
(λ
,
)
= λ
(
,
)
для любого действительного числа
;
40 ( , ) > 0, если .
Из условий 10 – 40 следует, что:
а) ( + , ) = ( , ) + ( , );
б) ( , λ ) = λ( , )
в) ( , ) = 0 для любого вектора .
Скалярное произведение любого вектора R на себя называется скалярным квадратом.
Длиной (нормой) вектора в евклидовом пространстве называется квадратный корень из скалярного квадрата этого вектора, т. е.
.
Если λ − любое действительное число, а − любой вектор евклидова пространства, то
.
Вектор, длина которого равна единице, называется нормированным. Если R − ненулевой вектор, то
является нормированным вектором.
Для любых двух векторов и в евклидовом пространстве выполняется неравенство
(или
)
− неравенство Коши-Буняковского.
Равенство
имеет место тогда и только тогда, когда векторы и линейно зависимы.
Угол φ между векторами и определяется равенством:
,
где 0
π
Если
и
− ненулевые векторы, а
,
то (
,
)
= 0. В этом случае говорят, что векторы
и
ортогональны,
т.е.
.
Для произвольных векторов и евклидова пространства имеют место важные соотношения:
( неравенство
треугольника ).Пусть φ − угол между векторами и , тогда
(теорема
косинусов).
Если
,
то
.
Заменяя в последнем равенстве на − , получим
(теорема Пифагора).
Пример.
Пусть
множество всевозможных систем
действительных чисел
,
,
,
… является линейным пространством.
Можно
ли скалярное произведение двух
произвольных векторов
и
определить равенством
( для того, чтобы это пространство стало
евклидовым)?
□ Для этого необходимо проверить выполнение условий 10 − 40.
10
Так как
(
,
)=
,
то
.
20
Пусть
.
Тогда
и
30
.
40
,
если
хотя бы одно из чисел
х1, х2 , …, хn отлично от нуля.
Значит, в заданном пространстве с помощью указанного равенства можно определить скалярное произведение. ■
Ортогональный базис
Базис , ,…, евклидова пространства называется ортогональным, если
при
.
Теорема. Во всяком евклидовом пространстве имеется ортогональный базис.
Если ортогональный базис состоит из нормированных векторов, то этот базис называется ортонормированным. Для ортонормированного базиса , ,…, справедливо
Если
в n -
мерном евклидовом пространстве известен
какой-нибудь базис
,
,…,
, то в этом пространстве всегда можно
найти и ортонормированный базис
,
,…,
.
Любой вектор евклидова пространства, заданный в ортонормированном базисе, определяется равенством:
.
Длина вектора находится по формуле
.
Два вектора
и
линейно зависимы ( коллинеарны, пропорциональны) тогда и только тогда, когда
.
Ортогональность двух векторов и :
.
Угол между двумя векторами и :
.
Пример. Нормировать вектор
.
□ Согласно
формуле
,
имеем
■
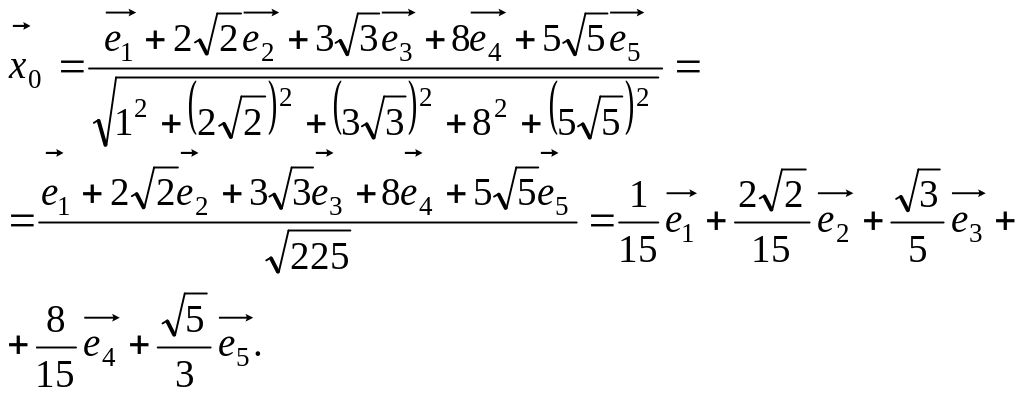
Пример.
Дана
матрица А
=
перехода
от ортонормированного базиса
,
,
к базису
*,
*,
*.
Доказать, что базис
*,
*,
*
ортонормированный.
□ Вспоминая переход к новому базису, можем записать
или
Для ортонормированного базиса , , должны выполняться равенства
Проверим эти равенства для базиса *, *, *:
Так как указанные равенства выполняются, то базис *, *, * − ортонормированный. ■
Пример. При каком значении λ базис, образованный векторами
,
,
,
является ортогональным? Нормировать этот базис.
□ Базис
будет ортогональным, если
при
.
В нашем случае, если
при
.
Пусть, например,
.
Тогда
Отсюда
λ = −1. Следовательно,
,
,
и
Пронормируем векторы полученного ортогонального базиса по формуле
,
где i
= 1,2,3,4.
Длина
равна:
.
Таким образом, векторы
,
,
,
образуют ортонормированный базис. ■
Ортогональные преобразования
Линейное преобразование (линейный оператор) А евклидова пространства называется ортогональным, если оно сохраняет скалярное произведение любых двух векторов и этого пространства, т.е.
.
Длина
вектора
при этом не изменяется, т.е.
.
Таким
образом,
.
Из последнего равенства следует, что ортогональное преобразование А не изменяет угла между любыми двумя векторами и .
Ортогональное преобразование переводит любой ортонормированный базис в ортонормированный. Наоборот, если линейное преобразование переводит какой-нибудь ортонормированный базис в ортонормированный, то оно является ортогональным.
Пример.
При
каком значении λ
преобразование А,
определяемое равенством
,
является ортогональным?
□ Пусть
,
,
,
.
Преобразование будет ортогональным, если
и
,
.
Тогда имеем
.
Это
равенство будет выполняться при
,
т.е. при
.
При таких значениях λ
не изменяются длины векторов
и
:
.
Если
,
то
.
Аналогично,
.
■
Пример.
Является
ли ортогональным преобразование А,
определяемое в каком-нибудь ортонормированном
базисе
матрицей
,
если
,
,
,
,
,
?
□ Составим
векторы
:
,
,
.
Если
,
,
то преобразование А
будет ортогональным. Проверим это
условие:
− по условию;
− по условию;
− по условию.
Значит, преобразование А − ортогональное.
Более того, т. к.
−
по
условию,
−
по
условию,
−
по
условию,
то векторы образуют ортонормированный базис. Это означает, что преобразование А − ортонормированное. ■