§ 10. Трехмерные векторы (векторы в пространстве)

Пусть вектор задан в трехмерном пространстве:

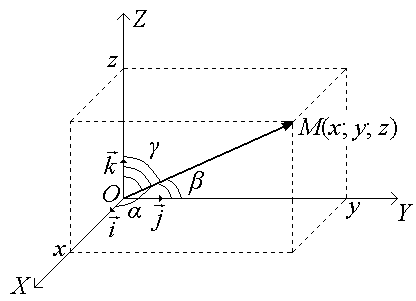
Очевидно, что для трехмерных векторов можно дать аналогичные определения и формулы.

Радиус-вектор:

= = (х; у; z) = х + у + z , (1)

| | = . (2)

Произвольный вектор :

= (а_х; а_у; a_z) = а_х + а_у + a_z , (3)

| | = . (4)

Вектор , имеющий начало в точке А(х₁; у₁; z₁) и конец в точке В(х₂; у₂; z₂):

= (х₂ − х₁; у₂ − у₁; z₂ − z₁) = (х₂ − х₁) + (у₂ − у₁) + (z₂ − z₁) , (5)

| | = . (6)

Направляющие косинусы:

, , , (7)

причем (свойство направляющих косинусов)

+ + = 1.

Сумма и разность векторов:

± = (а_х ± b_х; а_y ± b_y; а_z ± b_z) = (а_х ± b_х) + (а_y ± b_y) + ( а_z ± b_z) . (8)

Произведение вектора на число:

т = (та_х; та_у; та_z) = та_х + та_у + та_z . (9)

Нормирование вектора:

₀ = . (10)

Очевидно, что орты , и имеют следующие координаты:

= (1; 0; 0), = (0; 1; 0), = (0; 0; 1).

Пример. Дана точка М(5; −3; 4). Определить длину и направление ее радиус-вектора.

□ Изобразим в системе координат точку М и радиус-вектор = :

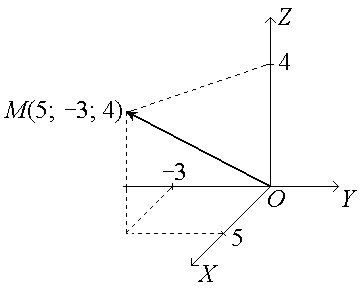
Запишем радиус-вектор :

= = (5; −3; 4) = 5 −3 + 4 .

По формуле ( 2 ) найдем его длину:

| | = = = = .

По формулам ( 7 ) найдем направляющие косинусы:

= = , = , = .

Зная направляющие косинусы, всегда можно найти углы α, β и γ, образованные радиус-вектором с осями координат OX, OY, OZ соответственно, т.е. определить направление вектора . ■

§ 11. Понятие п – мерного вектора. Линейное пространство

Обобщим понятие вектора.

п-мерным вектором называется упорядоченная совокупность п действительных чисел, записываемых в виде = (х₁, х₂,…, х_п), где

x_i – i-ая компонента (координата) вектора .

Сумма двух векторов одинаковой размерности п: если = (х₁, х₂,…, х_п) и = (у₁, у₂,…, у_п), то

= + = (х₁ + у₁, х₂ + у₂,…, х_п + у_п) = (z₁, z₂,…, z_п).

Произведение вектора на действительное число λ:

λ = (λх₁, λх₂,…, λх_п).

Линейные операции над любыми векторами удовлетворяют свойствам:

1⁰. + = + ;

2⁰. ( + ) + = + ( + );

3⁰. α(β ) = (αβ) ;

4⁰. α( + ) = α + α ;

5⁰. (α + β) = α + β ;

6⁰. существует нулевой вектор = (0, 0,…, 0) такой, что + =

для любого вектора ;

7⁰. для любого вектора существует противоположный вектор (− )

такой, что + (− ) = ;

8⁰. 1∙ = для любого вектора .

Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие свойствам 1⁰ − 8⁰, называется векторным пространством R.

Если под , , ,… рассматриваются не только векторы, но и элементы (объекты) любой природы, то такое множество элементов называют линейным пространством R.

Пример. Дано множество всевозможных пар положительных чисел:

= (х₁, х₂), = (у₁, у₂), = (z₁, z₂),… .

Является ли это множество линейным пространством, если сложение двух элементов определяется равенством

+ = (х₁у₁; х₂у₂),

а умножение на действительное число − равенством λ = ( )?

□ Проверим выполнение свойств 1⁰− 8⁰:

1⁰. + =(х₁у₁; х₂у₂), + =( у₁х₁; у₂х₂), т.е. + = + ;

2⁰. ( + ) + = ((х₁у₁)∙z₁; (х₂у₂)∙z₂) = (х₁у₁z₁; х₂у₂z₂),

+ ( + ) = (х₁(у₁z₁); х₂(у₂z₂)) = (х₁у₁z₁; х₂у₂z₂),

т.е. ( + ) + = + ( + );

3⁰. α(β ) = α( ) = ( ) = (αβ) ;

4⁰. α( + ) = ((х₁у₁)^α; (х₂у₂)^α) = (х₁^αу₁^α; х₂^αу₂^α) = α + α ;

5⁰. (α + β) = ( ) = (х₁^αх₁^β; х₂^αх₂^β) = α + β ;

6⁰. Нуль-элементом является пара положительных чисел = (1; 1), т.к.

+ = (х₁∙1; х₂∙1) = (х₁; х₂) = ;

7⁰. + (− ) = ((х₁; х₂) + (х₁⁻¹; х₂⁻¹) = (х₁∙х₁⁻¹; х₂∙х₂⁻¹) = (1; 1) = .

Получили нуль-элемент = (1; 1);

8⁰. 1∙ = (х₁¹; х₂¹) = (х₁; х₂) = .

Все свойства выполняются. Следовательно, заданное множество пар положительных чисел является линейным пространством. ■

Пусть , ,…, , − какие-нибудь векторы линейного пространства R.

Вектор , определенный равенством

= α₁ + α₂ + … + α_т−1 ,

где α₁, α₂,…, α_т−1 − действительные числа, называется линейной комбинацией векторов , ,…, .

Векторы , ,…, линейного пространства R называются

линейно независимыми, если из векторного равенства

α₁ + α₂ +…+ α_т = , (1)

где α₁, α₂,…, α_т − действительные числа, следует

α₁ = α₂ =… = α_т = 0.

Если же равенство (1) может выполняться и в том случае, когда не все числа α₁, α₂,…, α_т равны нулю, то говорят, что векторы , ,…,

линейно зависимы.

Очевидно, что векторы , ,…, линейно зависимы тогда и только тогда, когда один из этих векторов может быть представлен в виде линейной комбинации остальных векторов.

Пример. Являются ли векторы = (1;2) и = (3; 4) линейно независимыми.

□ Составим векторное равенство

α₁ + α₂ = .

Транспонируя строчные матрицы-векторы , , получим

α₁ + α₂ = .

Запишем систему уравнений

Полученная система однородная. Она всегда совместная.

Если определитель системы Δ ≠ 0, то система имеет единственное решение α₁ = α₂ = 0 и заданные векторы линейно независимы.

Если Δ = 0, то система неопределенная (имеет бесчисленное множество решений) и заданные векторы линейно зависимы.

Составим и вычислим определитель системы:

Δ = = 4 − 6 = −2 ≠ 0.

Значит, α₁ = α₂ = 0 и заданные векторы и являются линейно независимыми. ■

Замечание 1. Любые два неколлинеарных вектора на плоскости (двумерные векторы) линейно независимы.

Замечание 2. Любые три некомпланарных вектора в трехмерном пространстве (трехмерные векторы) линейно независимы.

Базис

Линейное пространство R называется п-мерным, если в нем существует п линейно независимых векторов, а любые п + 1 векторов этого пространства линейно зависимы.

Совокупность п линейно независимых векторов п-мерного пространства R называется базисом.

Теорема. Каждый вектор линейного пространства R можно представить и причем единственным способом в виде линейной комбинации векторов базиса.

Так, если , ,…, − базис п-мерного линейного пространства

R, то любой вектор R может быть единственным образом представлен в виде

= х₁ + х₂ + …+ х_п . (2)

Равенство (2) называют разложением вектора по базису , ,…, , а числа х₁, х₂,…, х_п координатами вектора относительно этого базиса.

Пример. В базисе , , заданы векторы = (1; 1; 0),

= (1; −1; 1), = (−3; 5; −6). Показать, что векторы , ,

образуют базис.

□ Векторы , , образуют базис, если они линейно независимы. Составим векторное равенство:

α₁ + α₂ + α₃ = ,

которое распишем в виде

α₁ + α₂ + α₃ = .

Получили систему

Составим и вычислим определитель системы

Δ = = 1∙ −1∙ = 1 + 3 = 4 ≠ 0.

Следовательно, α₁ = α₂ = α₃ = 0. Отсюда следует, что векторы , ,

линейно независимые, поэтому эти векторы образуют базис. ■

Замечание 1. Любой ненулевой вектор на прямой (одномерное пространство) является базисом на этой прямой;

Два неколлинеарных вектора на плоскости (двумерное пространство), взятых в определенном порядке, являются базисом на этой плоскости;

Три некомпланарных вектора в пространстве (трехмерное пространство), взятые в определенном порядке, являются базисом в этом пространстве.

Замечание 2. Координатные орты , на плоскости и , ,

в трехмерном пространстве образуют базисы. Поэтому запись

= а_х + а_у и = а_х + а_у + a_z часто называют разложением вектора по координатному базису.

Переход к новому базису

Пусть в п-мерном линейном пространстве R имеются два базиса: старый , ,…, и новый , ,…, . Пусть вектор

имеет координаты (х₁, х₂,…, х_п) в старом базисе и координаты

(х₁^*, х₂^*,…, х_п^*) в новом базисе. Тогда, если вектор в старом базисе записывается в виде

= х₁ + х₂ + …+ х_п ,

то в новом базисе он будет иметь вид:

= х₁^* + х₂^* + …+ х_п^* . (3)

После транспонирования строчных матриц-векторов , , ,…, получим систему уравнений, в которой неизвестными являются координаты (х₁^*, х₂^*,…, х_п^*) вектора в новом базисе , ,…, . Подставляя в (3) найденные координаты, получим выражение для вектора в новом базисе.

Пример. Вектор = (2; 3) задан в базисе , . Выразить вектор в новом базисе , , если = (1; 1), = (1; 2).

□ Вектор в новом базисе будет иметь координаты b₁^*, b₂^* , т.е.

= b₁^* + b₂^* .

Транспонируя строчные матрицы-векторы , , , получим

= b₁^* + b₂^* .

Составим систему

.

Решив систему, получим

Значит, вектор в новом базисе , будет иметь вид

= + . ■