§ 8. Понятие вектора

Вектором называется направленный отрезок с начальной точкой А и конечной точкой В, который можно перемещать параллельно самому себе

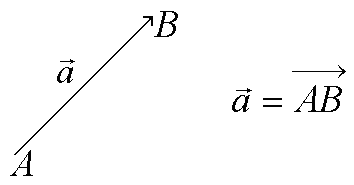
Длиной (модулем) | | вектора называется число, равное длине отрезка АВ, изображающего вектор.

Вектор называется нулевым, если начало и конец вектора совпадают: = , | | = 0.

Вектор называется единичным, если его длина равна 1, т.е. | | = 1.

Произведением вектора на число λ называется вектор = λ , имеющий длину | | = | λ|∙| |, направление которого совпадает с направлением вектора , если λ > 0, и противоположно ему, если λ < 0.

Противоположным вектором − называется произведение вектора на число (−1), т.е. − = (−1) .

Суммой двух векторов и называется вектор = + , начало которого совпадает с началом вектора , а конец − с концом вектора при условии, что начало вектора совпадает с концом вектора (правило треугольника):

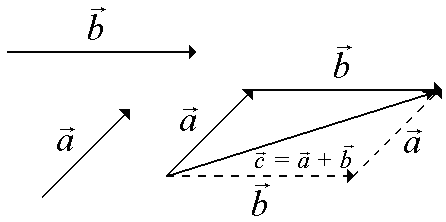
Очевидно, что вектор в этом случае представляет собой диагональ параллелограмма, построенного на векторах и (правило параллелограмма).

Аналогично определяется сумма нескольких векторов (правило многоугольника):

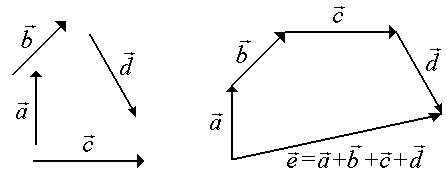
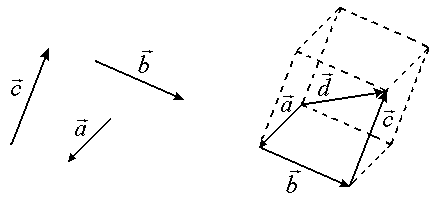
Суммой трех векторов в пространстве можно найти по правилу параллелепипеда. Суммой векторов , и является диагональ параллелепипеда, построенного на этих векторах, т.е. = + + :

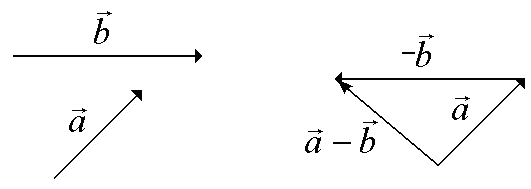
Разностью двух векторов и называется сумма вектора и вектора − , противоположного вектору :

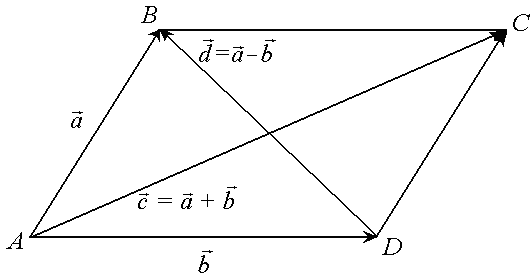
В параллелограмме, построенном на векторах = и = , одна диагональ – вектор = представляет собой сумму векторов и , а другая диагональ – вектор = − их разность:

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.

Векторы, лежащие в одной плоскости или на параллельных плоскостях, называются компланарными.

Два вектора называются равными, если они имеют равные модули, коллинеарны и направлены в одну сторону.

Проекция вектора на координатную ось, например на ось Ох, определяется по формуле:

пр_х = | |∙ ,

где φ − угол между вектором и осью Ох.

Свойства проекций:

пр_х( + ) = пр_х + пр_х ,

пр_х (α ) = α· пр_х , где α − число.

Сложение векторов и умножение вектора на число называются линейными операциями над векторами.

Свойства линейных операций

1⁰. Сложение векторов коммутативно, т.е. для любых векторов и выполняется + = + .

2⁰. Сложение векторов ассоциативно, т.е. для любых векторов и выполняется + ( + ) = ( + ) + .

3⁰. Прибавление нулевого вектора к любому вектору не меняет последнего + = .

4⁰. Для любого вектора вектор (−1) является противоположным, т.е. + (−1) = .

5⁰. Умножение вектора на число ассоциативно, т.е. для любых чисел α и β и любого вектора выполняется (αβ) = α(β ).

6⁰. Умножение вектора на число дистрибутивно по отношению к сложению чисел, т.е. для любых чисел α и β и любого вектора выполняется (α + β) = α + β .

7⁰. Умножение вектора на число дистрибутивно по отношению к сложению векторов, т.е. для любых векторов и и любого числа α выполняется α( + ) = α + α .

8⁰. Умножение вектора на единицу не меняет этого вектора, т.е. 1∙ = .

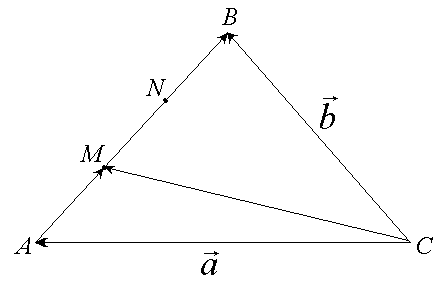
Пример. В ΔАВС сторона АВ точками М и N разделена на три равные части: |AM| = |MN| = |NB|. Найти вектор , если = , = .

□ Определимся еще с двумя векторами, необходимых для решения задачи. Пусть это будут векторы: и (можно было взять векторы и ).

По правилу треугольника имеем = + , т.е. = + . Отсюда = − . Так как |AM| = |MN| = |NB|, то = = . Из векторного треугольника АМС имеем = + = + = . ■