§ 6. Приведение общего уравнения поверхности второго порядка к каноническому виду

В общем случае для приведения общего уравнения поверхности второго порядка к каноническому виду используют квадратичные формы (ортогональные преобразования). Для этого следует:

а) найти линейное ортогональное преобразование, которое приводит квадратичную форму старших членов уравнения поверхности к сумме квадратов, и выполнить в уравнении соответствующую замену. В результате из уравнения исчезают члены с произведениями координат;

б) произведя после этого параллельный перенос новых осей координат (в пространстве иногда приходится, кроме того, делать дополнительный поворот двух осей в одной из координатных плоскостей), приводят уравнение к требуемому виду.

Пример. Привести к каноническому виду уравнение поверхности

3x² + 5y² + 3z² − 2xy + 2xz − 2yz −12x −10 = 0.

□ Здесь

f(x, y, z) = 3x² + 5y² + 3z² −2xy + 2xz − 2yz.

Матрица этой квадратичной формы имеет вид

.

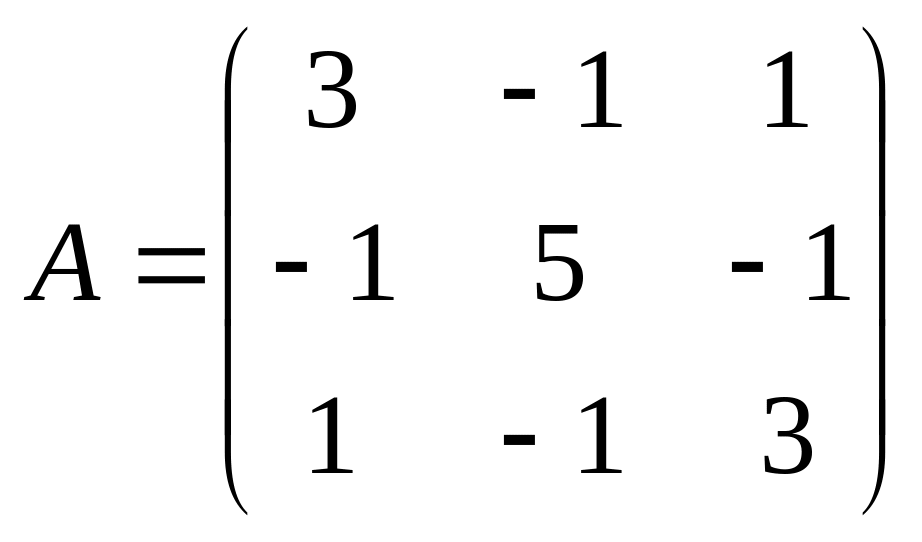Составим характеристическое уравнение

,

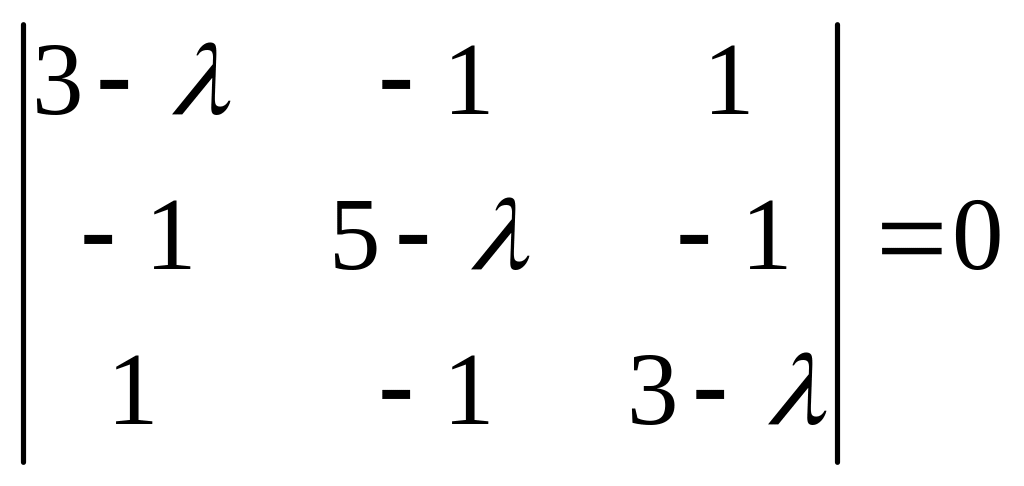которое приводится к виду

.

Отсюда находим .

При получаем систему

откуда получаем собственный вектор

При получаем систему

Отсюда находим собственный вектор

При получаем систему

Отсюда находим собственный вектор

Нормируя векторы, получим

, ,

.

Матрица ортогонального преобразования:

В = .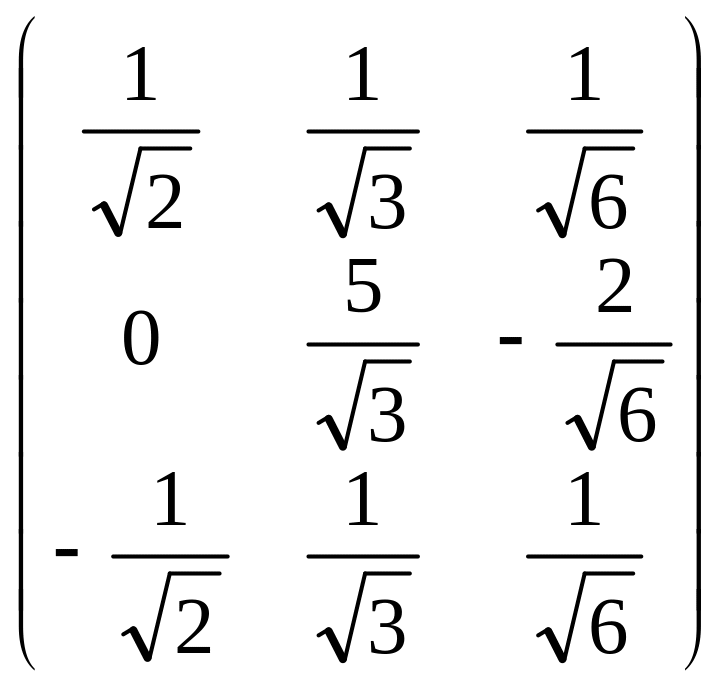

Отсюда получаем формулы преобразования координат:

Подставив выражения для x, y и z в уравнение поверхности, после упрощений получим

.

Коэффициентами при ², ² и ², как и должно быть, являются соответственно числа . Перепишем уравнение в виде:

.

После дополнения выражений в скобках до полных квадратов получим

.

Произведя параллельный перенос осей координат по формулам

, , ,

т. е. приняв за новое начало координат точку и разделив уравнение на 24, приходим к каноническому уравнению эллипсоида

■

Рассмотрим случай, когда уравнение поверхности не содержит произведения координат.

Отметим, что преобразование параллельного переноса декартовых координат в пространстве осуществляется так же, как и на плоскости.

Пример. Привести к каноническому виду уравнение

х² − у² − 4x + 8y −2z = 0.

□ Сгруппируем члены, содержащие х и у:

(х² − 4x) − (у² − 8y) = 2z.

Дополним до полных квадратов выражения в скобках:

(х² − 4x + 4) − (у² − 8y + 16) = 2z + 4 − 16

или

(х − 2)² − (у − 4)² = 2(z − 6).

Проведем параллельный перенос осей координат, приняв за новое начало точку (2; 4; 6). Тогда преобразования координат имеют вид

= х − 2, = у − 4, = z − 6.

В результате получаем уравнение

− = 2 ,

определяющее гиперболический параболоид. ■

Иногда для упрощения уравнения кривой можно воспользоваться другими методами

Пример. Каков геометрический смысл уравнения

?

□ Данное уравнение можно записать в виде

.

Получили квадратное уравнение относительно скобки . Разложив на множители левую часть уравнения, получим

.

Таким образом, заданное уравнение определяет совокупность двух плоскостей:

и . ■

Пример. Какую поверхность определяет уравнение

?

□ Преобразуем заданное уравнение:

, , .

Это уравнение распадается на два: и , т.е. оно определяет две плоскости: координатную OXZ и плоскость , проходящую через ось OX. ■