§ 4. Кривые второго порядка

Уравнение

Ах² + 2Вху + Су² + 2Dx + 2Ey + F = 0, (1)

где А, В, С, D, E, F − заданные действительные числа, при этом А, В, С одновременно не равны нулю, называется общим уравнением кривой второго порядка.

Может случиться, что нет вовсе точек (х; у) с действительными координатами, удовлетворяющих уравнению (1). В этом случае говорят, что уравнение (1) определяет мнимую кривую второго порядка.

Окружность

Окружностью называется геометрическое место точек, равноудаленных от данной точки (центра).

Если r – радиус окружности, а точка С(а; b) – ее центр, то уравнение окружности имеет вид

(х – а)² + (у – b)² = r². (2)

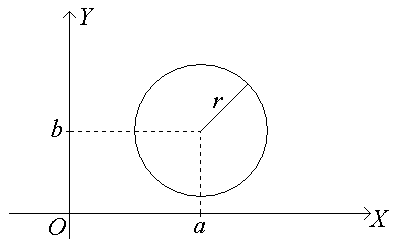
В частности, если центр окружности совпадает с началом координат, то последнее уравнение примет вид

х² + у² = r²,

т.к. в этом случае а = b = 0.

Пример. Привести к каноническому виду уравнение

х² + у² – 8х + 6у = 0.

□ Выделим в левой части заданного уравнения полные квадраты:

(х² − 2∙4х + 16) – 16 + (у² + 2∙3у + 9) − 9 = 0,

(х – 4)² + (у + 3)² − 25 = 0.

Окончательно, получим

(х – 4)² + (у + 3)² = 5².

Таким образом, получили уравнение окружности с центром С(4; −3) и радиусом r = 5. ■

Эллипс

Эллипсом называется геометрическое место точек, сумма расстояний которых до двух точек F₁ и F₂ (фокусов) есть величина постоянная, равная 2а.

Каноническое уравнение эллипса имеет вид

+ = 1. (3)

Пусть а > b > 0. Тогда кривая будет иметь вид:

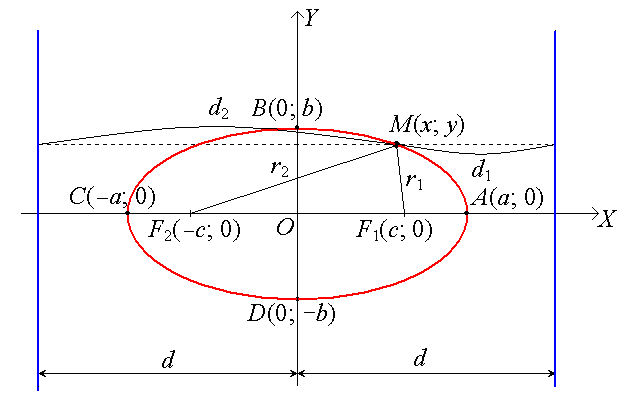
Кривая симметрична относительно осей OX и OY.

Точки А(а; 0), B(0; b), C(−a; 0), D(0;−b) − вершины эллипса;

а – большая полуось (2а–большая ось);

b – малая полуось (2b – малая ось).

Если а = b, то эллипс (3) обращается в окружность радиуса а и с центром в начале координат: х² + у² = а².

Точки F₁(c; 0), F₂(−c; 0) – фокусы, лежащие на оси ОХ, где

с = .

Отношение = ε – эксцентриситет эллипса. Так как с < a, то ε < 1. Эксцентриситет характеризует меру сжатия эллипса: при ε → 0 а → b и форма эллипса близка к окружности; при ε → 1 – эллипс сильно вытянут вдоль оси ОХ.

Расстояния r₁ и r₂ от некоторой точки М(х; у) до фокусов называют фокальными радиус-векторами этой точки. Их можно вычислить по формулам:

r₁ = а – εх, r₂ = а + εх,

где х – абсцисса точки М.

Отметим, что из определения эллипса следует

r₁ + r₂ = 2а.

Директрисы эллипса – прямые, параллельные малой оси, находящиеся на расстоянии d = от нее.

Директориальное свойство эллипса:

Для любой точки М(х; у) эллипса

= = ε.

Если b > a > 0, то эллипс вытянут вдоль оси OY и его фокусы лежат на OY. С этим связаны соответствующие изменения в написанных формулах.

Пример. Составить уравнение эллипса, проходящего через точки М( ; ) и N(−2; ).

□ Каноническое уравнение эллипса имеет вид

+ = 1.

Этому уравнению должны удовлетворять координаты данных точек. Следовательно,

Решая систему относительно а² и b², получим а² = 10, b² = 1.

Искомое уравнение эллипса имеет вид

+ = 1

или

+ = 1. ■

Гипербола

Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых до двух точек F₁ и F₂ (фокусов) есть величина постоянная, равная 2а.

Каноническое уравнение гиперболы имеет вид

− = 1, (4)

где a, b > 0.

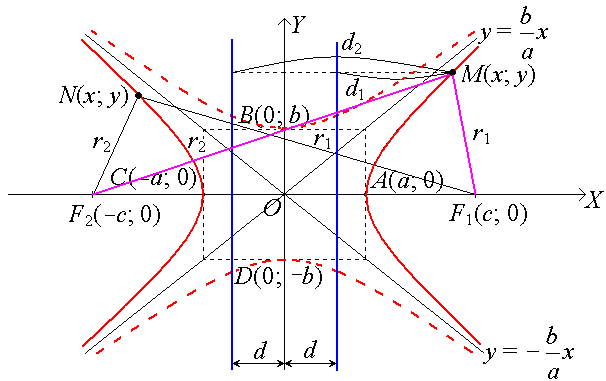
Кривая симметрична относительно осей OX и OY.

Точки А(а; 0), C(−a; 0) − вершины гиперболы;

а – действительная полуось (2а – действительная ось);

b – мнимая полуось (2b – мнимая ось).

Точки F₁(c; 0), F₂(−c; 0) – фокусы, лежащие на оси ОХ, где

с = .

Отношение = ε – эксцентриситет гиперболы. Так как с > a, то

ε > 1. Чем меньше эксцентриситет, тем ближе ветви гиперболы к оси ОХ.

Прямые у = х – асимптоты гиперболы.

Фокальные радиус-векторы правой ветви гиперболы (точки М(x; y)):

r₁ = εх − а, r₂ = εх + а,

где х – абсцисса точки М.

Фокальные радиус-векторы левой ветви гиперболы (точки N(x; y)):

r₁ = − εх + а, r₂ = − εх − а,

где х – абсцисса точки N.

Отметим, что из определения гиперболы следует

|r₁ − r₂| = 2а.

Если а = b, то уравнение гиперболы (4) примет вид х² − у² = а² − равносторонняя гипербола. Ее асимптоты взаимно перпендикулярны.

Гиперболы

− = 1 и − = −1

называются сопряженными. Они имеют одни и те же полуоси и одни и те же асимптоты, но действительная полуось одной служит мнимой полуосью другой, и наоборот.

Директрисы гиперболы – прямые, перпендикулярные к действительной оси, находящиеся на расстоянии d = от центра.

Директориальное свойство гиперболы:

Для любой точки М(х; у) гиперболы

= = ε.

Пример. Установить, какая линия определяется уравнением

у = −3 .

□ Проведем следующие преобразования:

у² = 9(х² + 1) = 9 х² + 9,

9 х² − у² = −9, − = −1.

Окончательно, получим

− = −1.

Получили каноническое уравнение гиперболы. Так как по условию задачи у принимает только отрицательные значения, то первоначальная запись уравнения определяет не всю гиперболу, а лишь ту ее часть, которая лежит ниже оси ОХ. ■

Парабола

Параболой называется геометрическое место точек, одинаково удаленных от точки F (фокуса) и прямой (директрисы).

Каноническое уравнение параболы имеет два вида:

1) у² = 2рх. (5)

Если параметр р > 0, то кривая имеет вид

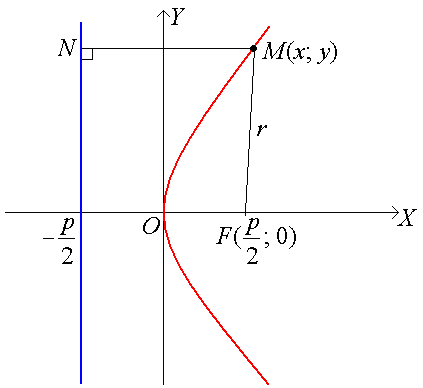
Кривая симметрична относительно оси ОХ. Из определения параболы следует, что MN = MF. У параболы (5) F( ; 0) − фокус; прямая х = − − директриса; r = x + − фокальный радиус-вектор точки М(x; y), где х − абсцисса точки М.

2) Парабола

х² = 2ру ( )

симметрична относительно оси ОY. У этой параболы (р > 0): F(0; ) − фокус; прямая у = − − директриса; r = у + − фокальный радиус-вектор точки М(x; y), где у − ордината точки М.

Если р > 0, то ветви парабол (5) и ( ) обращены в положительную сторону соответствующей оси; при р < 0 − в отрицательную сторону.

Пример. Вычислить фокальный радиус-вектор точки М(x; y) параболы

у² = 20х,

если абсцисса точки М равна 7.

□ Каноническое уравнение параболы в данном случае имеет вид

у² = 2рх. Следовательно,

у² = 20х = 2∙10х, т.е. р = 10.

Фокальный радиус-вектор можно вычислить по формуле r = x + .

Значит, r = 7 + = 12. ■