§ 2. Многочлены

Функция

называется многочленом п-ой степени ( полиномом п-ой степени ) или целой рациональной функцией от х.

Здесь

п − степень многочлена (целое число);

А₀, А₁, А₂, … , А_п − коэффициенты ( действительные или комплексные числа);

х − переменная ( может принимать как действительные, так и комплексные значения).

Значение переменной х, при котором многочлен обращается в ноль − корень многочлена.

Теорема 1 (теорема Безу). При делении многочлена f (x) на разность х − а получается остаток, равный f (а).

○ При делении многочлена f(x) на х − а частным будет многочлен f₁(x), степень которого на единицу ниже степени f (x), остатком будет постоянное число R. Таким образом,

. (1)

Это равенство справедливо при всех значениях х, отличных от а.

Пусть . Тогда

или . ●

Следствие. Если а является корнем многочлена, т.е. , то

f (x) делится без остатка на х − а и, следовательно, представляется в виде

,

где f₁(x) − многочлен.

Теорема 2 (основная теорема алгебры). Всякая целая рациональная функция f(x) имеет по крайней мере один корень, действительный или комплексный.

Теорема 3. Всякий многочлен п-ой степени разлагается на п линейных множителей вида х − а и множитель, равный коэффициенту при .

○ Пусть имеется многочлен

.

В силу основной теоремы он имеет по крайней мере один корень. Пусть это а₁ . Тогда из следствия теоремы Безу следует

,

где f₁(x) − многочлен (п − 1)-ой степени; f₁(x) также имеет корень. Пусть это а₂ . Тогда

,

где f₂(x) − многочлен (п − 2)-ой степени. Продолжая эту процедуру, в конце получим

,

где f_п − многочлен нулевой степени, т.е. некоторое фиксированное число. Это число, очевидно, равно коэффициенту при , т.е. f_п = А₀.

Таким образом,

. (2)

Из (2) следует, что числа а₁, а₂, … , а_п − корни многочлена f(x). ●

Многочлен п-ой степени не может иметь более п различных корней.

Если в разложении многочлена п-ой степени на линейные множители

некоторые линейные множители окажутся одинаковыми, тоих можно объединить, и тогда

.

При этом

.

В этом случае корень а₁ называется корнем кратности k₁ или k₁-кратным корнем, а₂ − корнем кратности k₂ и т.д.

В (2) корни а₁, а₂, … , а_п могут быть как действительные, так и комплексные.

Теорема 4. Если многочлен f(x) с действительными коэффициентами имеет комплексный корень , то он имеет и сопряженный корень .

○ Если подставить в f(x) вместо х число , возвести в степень и собрать отдельно члены, содержащие i и не содержащие i, то получим

,

где M и N − выражения, не содержащие i .

Так как − корень многочлена, то

= 0.

Отсюда следует, что М = 0, N = 0.

Подставим теперь в f(x) вместо х число . Мы получим в результате число, сопряженное с числом , т.е.

.

Так как М = 0, N = 0, то , т.е. есть корень многочлена f(x). ●

Таким образом, в разложении

комплексные корни входят попарно сопряженными.

Перемножив линейные множители, соответствующие паре комплексно сопряженных корней, получим трехчлен второй степени с действительными коэффициентами:

= = =

= = ,

где − действительные числа.

Если число является корнем кратности k, то сопряженное число должно являться корнем той же кратности k, так что наряду с линейными множителями в разложении многочлена входят столько же линейных множителей вида .

Таким образом, многочлен с действительными коэффициентами разлагается на множители с действительными коэффициентами первой и второй степени соответствующей кратности, т.е.

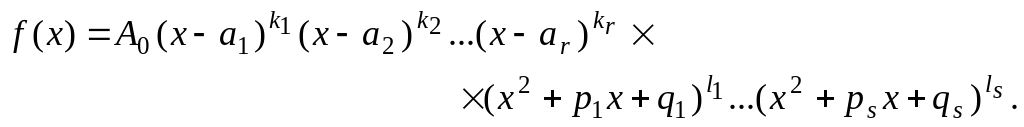
При этом

.

Разложение правильной рациональной дроби на простейшие

Отношение двух алгебраических многочленов

(3)

где , , В₀, А₀ ≠ 0,

называется рациональной функцией или рациональной дробью.

Будем считать, что рациональная дробь f(x) действительная, т.е. и − действительные многочлены, х − действительная переменная.

Рациональные функции (рациональные дроби) вида

, , , , (4)

где А, М, N, а, p, q − действительные числа, k − натуральное число, а трехчлен не имеет действительных корней называются простейшими дробями.

Будем считать, что рациональная дробь f(x) правильная, т.е.степень ее числителя меньше степени знаменателя ( т < n ).

Теорема 5. Пусть знаменатель правильной действительной рациональной дроби разложен по формуле :

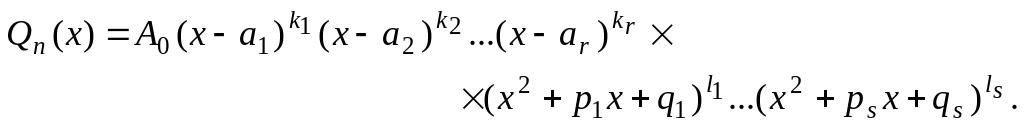
Тогда дробь (3) можно представить и притом единственным образом в виде следующей суммы простейших дробей:

+ + … + + +

+ + … + + … + + +

+ … + + + + …+

+ + … + + +

+ … + .

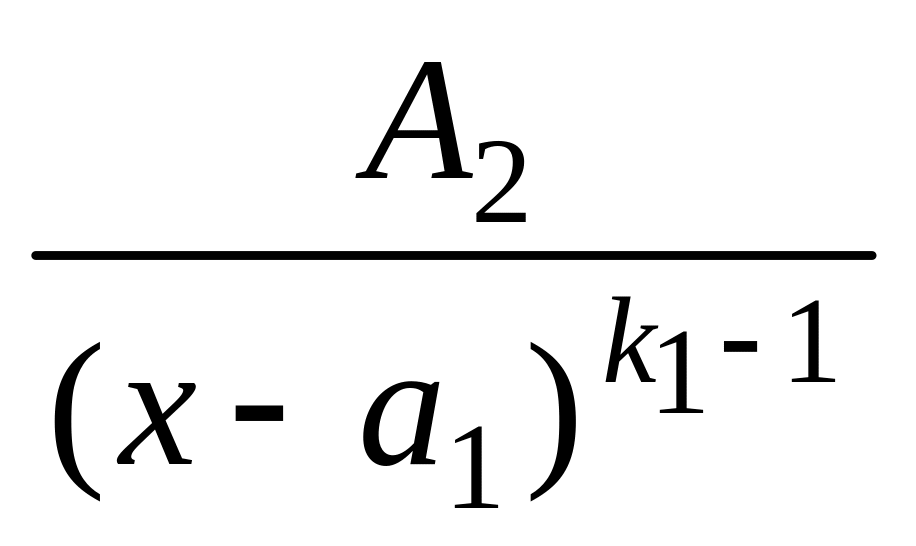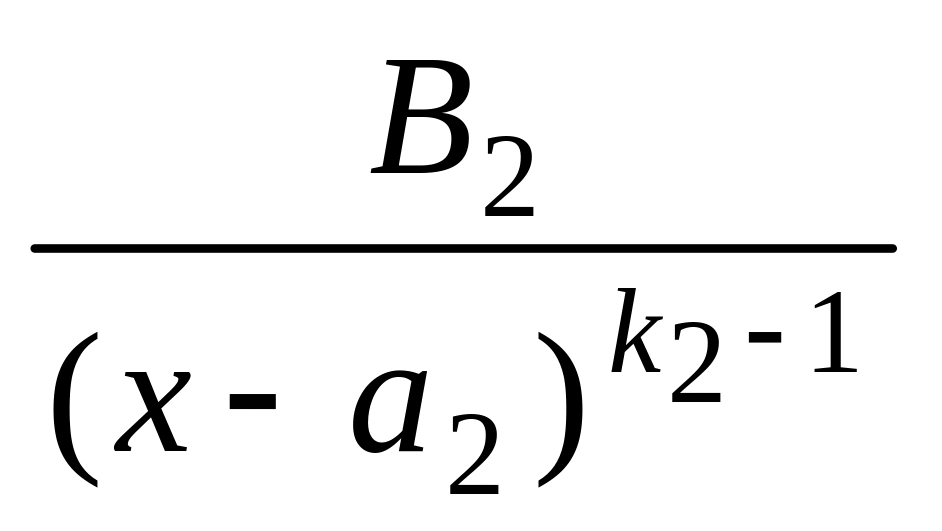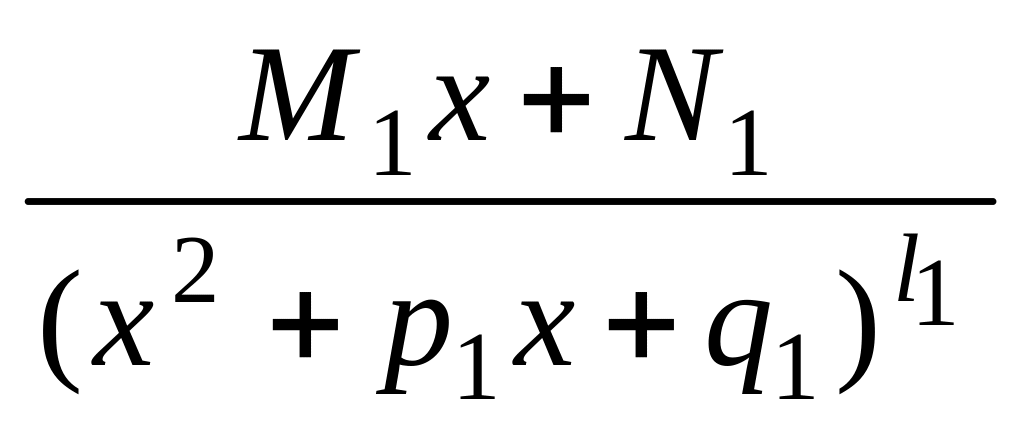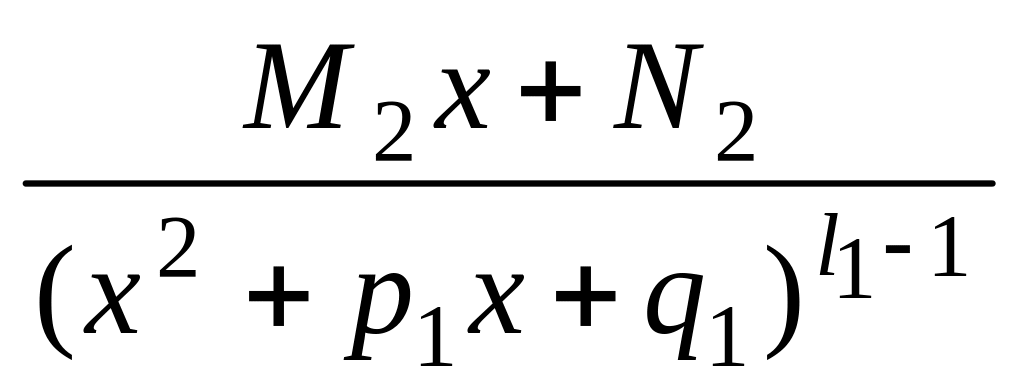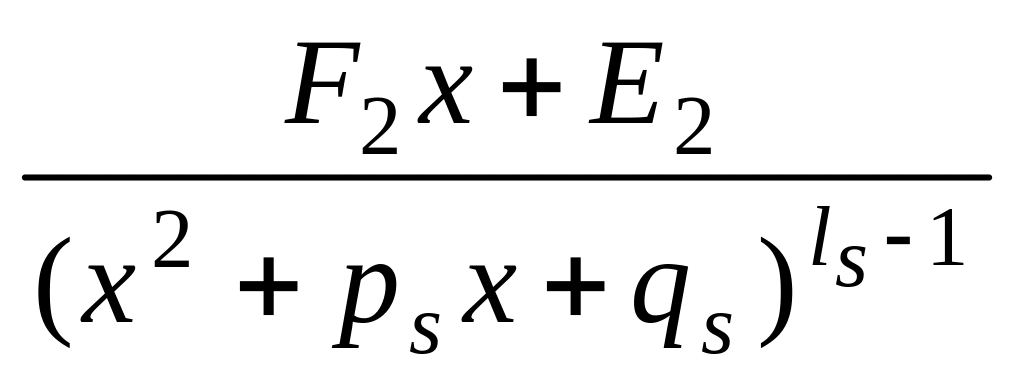Коэффициенты А₁, А₂, … , , B₁, B₂, … , , … , C₁, … , , M₁, N₁, M₂, N₂, … , , , … , F₁, E₁, F₂, E₂, … , , можно определить с помощью метода неопределенных коэффициентов :

написанное равенство есть тождество, поэтому, приведя дроби к общему знаменателю, получим тождественные многочлены в числителях справа и слева от знака равенства. Приравнивая коэффициенты при одинаковых степенях х, получим систему уравнений для определения неизвестных коэффициентов А₁, А₂, … , , B₁, B₂, … , , … , C₁, … , , M₁, N₁, M₂, N₂, … , , , … , F₁, E₁, F₂, E₂, … , , .

Пример. Разложить правильную рациональную дробь

на сумму простейших дробей.

□ Учитывая, что квадратный трехчлен не имеет действительных корней, получим

= + + =

= .

Приравниваем числители

= .

После раскрытия скобок и приведения подобных членов, получим:

= .

Приравнивая коэффициенты при одинаковых степенях х, получим систему уравнений

Отсюда

Таким образом,

= + + . ■

Замечание. Если рациональная дробь неправильная ( т n ), то делением числителя на знаменатель можно получить сумму некоторого многочлена и правильной рациональной дроби, которую можно разложить на простейшие дроби.

Пример. Разложить правильную рациональную дробь

на сумму простейших дробей.

□ Дробь неправильная, т.к. т > n. Деля числитель на знаменатель, получим

= х + .

Дробь − правильная и ее можно разложить на сумму простейших дробей. В результате получим

= х + + − + . ■