2.5. Условия однозначности.

Общее решение дифференциального уравнения невозможно, а для получения частных решений в каждом конкретном случае, необходимо математически задать качественные и количественные условия протекания процесса теплопроводности. Эти частные условия протекания процесса теплопроводности в данном конкретном случае называются условиями однозадачности, или краевыми условиями. Т.к. эти условия в совокупности определяют только один случай протекания процесса теплопроводности, то они так же называются условиями единственности, а решаемая с их помощью задача называется краевой задачей.

Краевые условия делятся на начальные и граничные.

Начальные условия дают распределение температур в теле в момент времени =₀ (обычно ₀=0)­

Граничные условия задаются тремя способами:

Граничные условия 1-го рода задаются значением распределения температур всей поверхности тела в функции от времени.

Граничные условия 2-го рода задаются значением распределения плотности теплового потока каждой точке поверхности тела в функции от времени.

Граничные условия 3-го задаются значением распределения температуры среды, окружающей тело, и закономерностями теплообмена между средой и поверхностью тела.

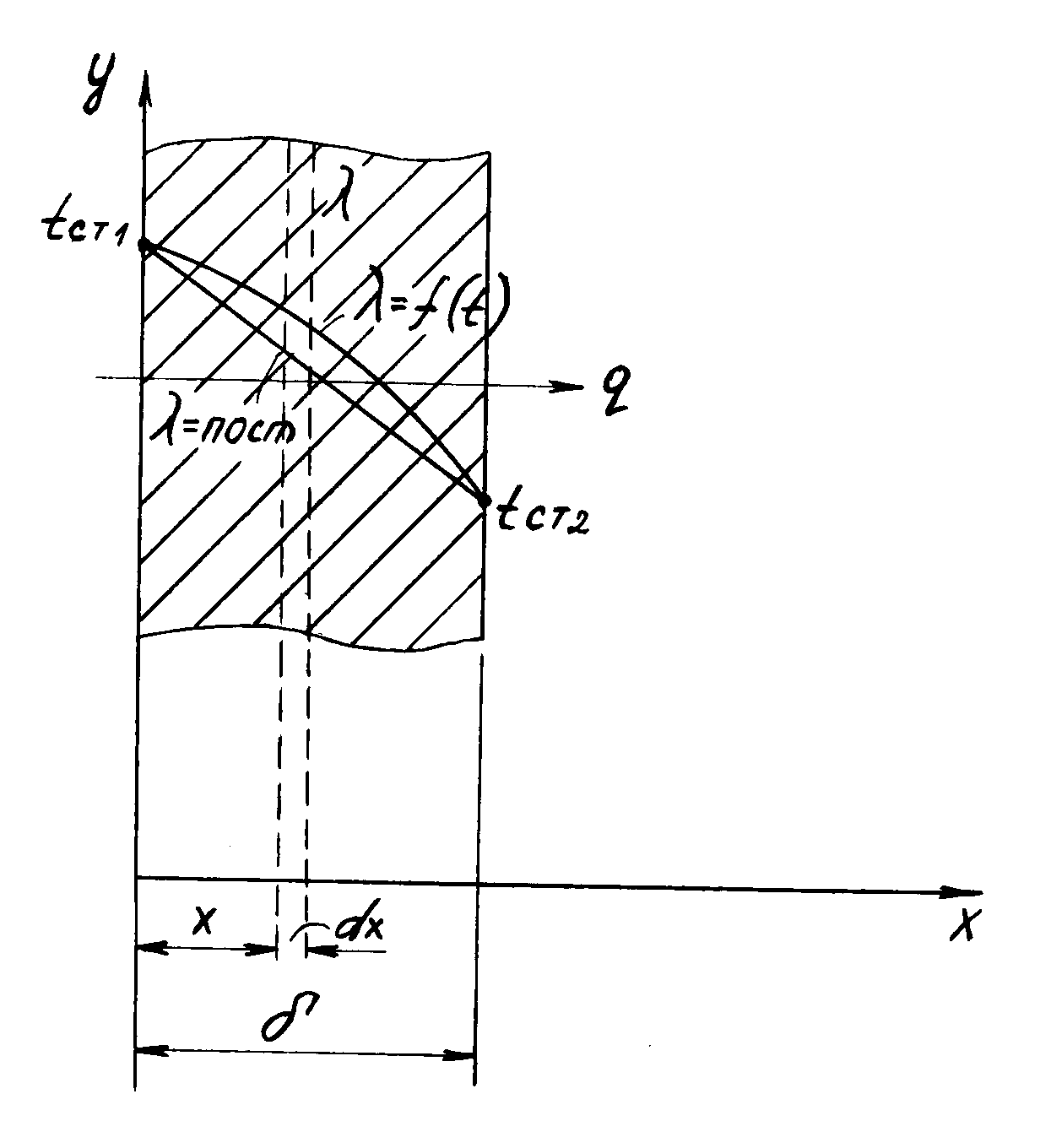
2.6. Теплопроводность однослойной плоской стены при стационарном режиме и граничных условиях 1-го рода.

Рассмотрим однородную однослойную плоскую стенку больших размеров и относительно малой толщиной [] (Рис. 4).

Граничные условия 1-го рода по всей поверхности. Тогда температура меняется только по оси х, т.е. поле одномерное. Изотермические поверхности в этом поле будут плоскости перпендикулярные оси х ( и по условию). Тепловой поток q=пост, т.к. площадь изотермических поверхностей постоянна, а процесс стационарный.

Рассмотрим решение при

двух условиях =пост, и =f(t)

2.6.1. Решение при =пост.

Из дифференциального уравнения теплопроводности, при q_V=0, ,

, получим для одномерного стационарного поля или . Интегрируя первый раз имеем

, где С₁ - первая постоянная интегрирования.

После повторного интегрирования имеем

описание температурного поля внутри плоской стенки t=C₁x+C₂, где С₂ - вторая постоянная интегрирования.

Задавая граничные условия 1-го рода найдем постоянные интегрирования

при х=0 t=t_cm1 и при х= t=t_cm2 Подставляя принятые граничные условия в уравнение температурного поля внутри плоской стенки получим

C₂=t_cm1 и t_cm2=C₁+t_cm1, откуда

.

Подставляя значения величин С₁ и С₂ получим окончательное значение уравнения температурного поля

.

Из уравнения Фурье найдем удельный тепловой поток для одномерного поля

. Т.к. , то из этого уравнения величина теплового потока равна .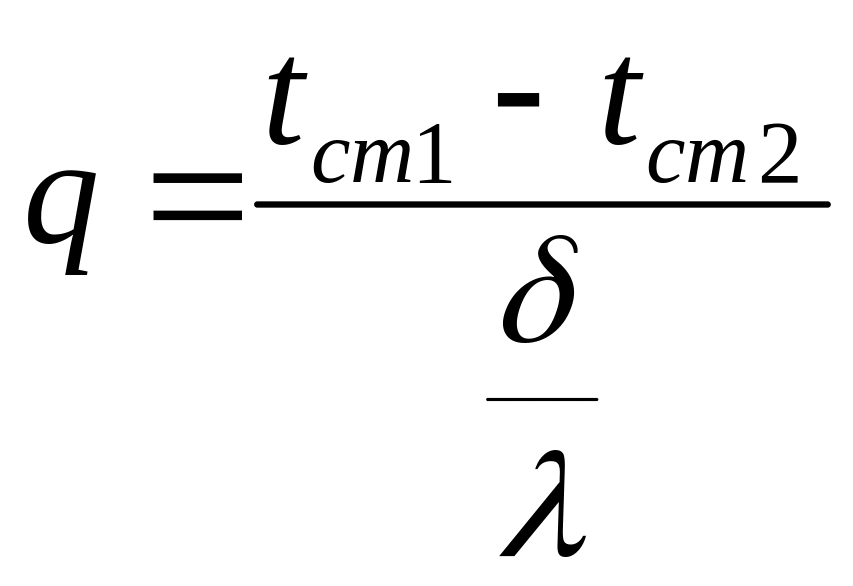

Выразив , имеем уравнение температурного поля

При q=пост и =пост, это уравнение прямой линии.

Обозначим отношение и назовем его удельным термическим сопротивлением плоской стенки, размерность

, тогда уравнение удельного теплового потока будет равно

Данное уравнение имеет аналогию с законом Ома для электрического проводника, где q- соответствует силе тока, t_cm1-t_cm2 разности напряжений и R - электрическому сопротивлению проводника.

Полный тепловой поток через плоскую стенку площадью F, м²

2.6.2. Решение при =f(t)

В большинстве случаев эта зависимость линейная и можно принять =₀(1+bt)

где ₀ - коэффициент теплопроводности при t=0 С;

b - эмпирический коэффициент.

Подставляя  в уравнение Фурье имеем

Разделяем переменные

.

После интегрирования имеем уравнение температурного поля

где С - постоянная интегрирования;

х - текущая координат в стенке, м;

t - температура в точке с координатой x, С.

Постоянную интегрирования определяем из граничных условий 1-го рода, при

х=0 t=t_cm1, при x= t=t_cm2. Подставляя 1-ое условие в уравнение температурного поля получим значение величины С

и

Подставляя 2-ое , также получим значение С.

и

Приравнивая полученные значения С, найдем уравнение теплового потока

,

,

Анализ уравнения показывает, что величина теплового потока остается постоянной по всей толщине стенки. Обозначим средний интегрирующий коэффициент теплопроводности

,

тогда уравнение теплового потока равно

или

,

где R_ср - среднее термическое сопротивление стенки, равное

Уравнение температурного поля получим подставив значение С, полученное из 1-го граничного условия

.

Преобразуем полученное выражение в квадратное уравнение и разделив все члены на , получим

.

Решая квадратное уравнение имеем

окончательное уравнение температурного поля при =f(t) будет иметь вид

Это параболическая зависимость.