2.4. Дифференциальное уравнение теплопроводности.

При изучении процесса теплопроводности для описания сложных зависимостей температурного поля в целом используют методы математической физики.

Для этого, в рассматриваемом поле выделяют элементарный объем вещества в бесконечно малый промежуток времени и описывают тепловое равновесие в этом объеме.

За счет бесконечно малой величины объема и отрезка времени можно пренебречь изменением физических параметров вещества в элементарном объеме, что значительно упрощает зависимость между параметрами процесса.

Связь между бесконечно малыми изменениями параметров теплопроводности в произвольном элементарном объеме называется дифференциальным уравнением теплопроводности.

При выводе этого уравнения принимаются следующие допущения: рассматриваемое тело однородно и изотропно, так же подчиняется закону сохранения энергии.

Рассмотрим элементарный объем в форме параллелепипеда с ребрами dx, dy, dz (Рис. 2). Тепловой поток dQ разложим по осям dQ_x, dQ_y, dQ_z и обозначим по каждой оси входящий в объем поток тепла dQ_x1, а выходящий dQ_x2 и т.д. Тогда остаток теплового потока в элементарном объеме

dQ_x= dQ_x1 - dQ_x2 и т.д.

О бозначив количества тепла, выделяемого в данном объеме за счет внутренних источников тепла (например электрический ток, химические реакции, ТВЭЛ атомных ректоров и др.) dQ_вн.ист. и изменение внутренней энергии данного элементарнго объема вещества через dU, можем записать закон сохранения энергии в дифференциальной форме

dU= dQ_вн.ист.+ dQ_x+ dQ_y+ dQ_z

Величины dQ в уравнении определяются в соответствии с законом Фурье для одномерного поля за время d.

По оси х при градиенте температуры и площади входной и выходной грани dу, dz

для темпертуры на входной грани t_x=t

для температуры выходной грани .

Раскрывая скобки имеем

.

Аналогично получим

,

.

Обозначив удельную объемную мощность внутренних источников тепла [Вт/м³] получим тепловыделение dQ_вн.ист. равное за время d

Изменение внутренней энергии за счет: массовой теплоемкости - С, массы вещества в, объем - dх dу dz  и изменения температуры за время будет равно

Подставляя полученные выражения в исходные уравнения имеем

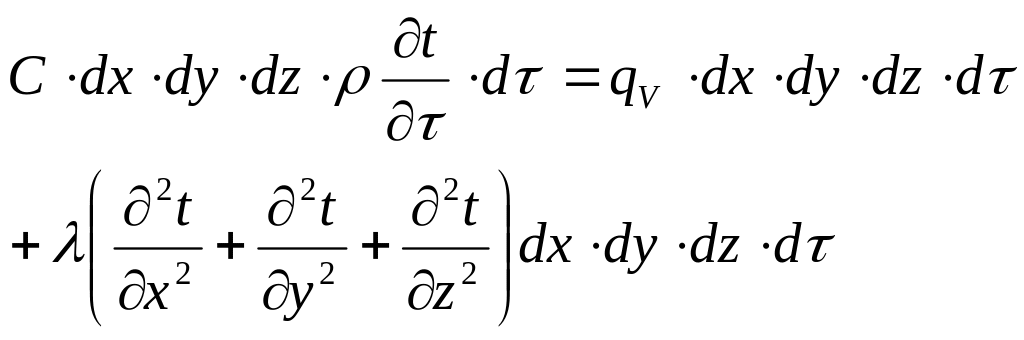
Сокращая одинаковые множители и разделив обе части на С имеем

Полученное уравнение называется дифференциальным уравнением теплопроводности или уравнением Фурье для трехмерного нестационарного температурного поля. Оно является основой аналитической теории теплопроводности и устанавливает связь между временным и пространственным изменением температуры в любой точке поля.

Величина

называется - коэффициент температуропроводности и является важным физическим параметром вещества. Коэффициент а характеризует скорость изменения температуры и чем больше а, тем быстрее изменяется температура тела во времени.

Значения а для металлов 170-1710^-6 м²/с, для твердых тел 0,8-0,110^-6, для жидкостей 0,1310^-6 (вода) для газов 1820 10^-6.

Величина в скобках называется оператором Лапласа и сокращенно обозначают знаком ² (набла), тогда дифференциальное уравнение теплопроводности имеет вид:

1 . для трехмерного нестационарного поля с внутренним источником тепла;

2. для трехмерного нестационарного поля без внутреннего источника тепла q_V=0;

3. для трехмерного стационарного поля при .

Анализ полученных уравнений показывает, что физический смысл величины и т.д. есть скорость изменения величины градиента температуры по оси х и т.д.

Тогда если >0, то в уравнении (2) >0 и следовательно имеет место нагрев - увеличение температуры в теле с течением времени (Рис. 3). Наоборот если <0 температура в теле снижается - режим охлаждения.

Если градиент температуры , то и и следовательно режим стационарный