2.2. Основные кинематические способы определения движения точки

Определить движение точки значит установить закон, которому под­чиняется ее движение, и который позволил бы найти положение точки в пространстве относительно выбранной системы отсчета в любой момент времени. Существует три основных кинематических способа определения движения точки:

векторный, координатный, естественный.

2.2.1.Векторный способ

Пусть точка М (рис. 2.3), движение которой подлежит определению, двигаясь в пространстве относительно некоторой системы отсчета O x y z, описывает траекторию АВ.

Из какой-нибудь точки, неизменно связанной с этой системой отсчета, напри­мер, из начала координат О, проведем в точку М радиус-вектор r. Понятно, что при движении точки М вектор r, в общем слу­чае, непрерывно изменяет как свою вели­чину (модуль), так и направление. Следо­вательно, он является векторной функцией времени , т.е. r = f(t) (2.3)

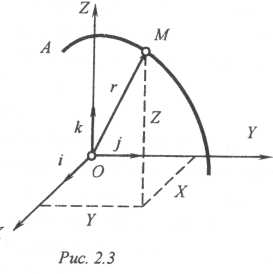
Это векторное равенство выражает закон движения точки М и называется векторным уравнением ее движения. Оно позволяет для любого момента времени построить вектор r (например, по его проекциям на координатные оси) и, следовательно, найти положение точки М относительно выбранной системы отсчета. Траектория точки М представляет собой годограф ее радиуса-вектора r. Функция (2.3) должна быть непрерывной, однозначной и дважды дифференцируемой.

2.2.2. Координатный способ

Известно, что положение точки в пространстве однозначно опреде­ляется тремя ее координатами: х, у, z относительно выбранной системы координат x O y z (рис. 2.3). При движении точки по траектории, в общем слу­чае, непрерывно изменяются с течением времени все три ее координаты. Таким образом, движение точки описывается уравнениями:

X=f₁ (t), У'= f₂ (t). Z=f₃ (t). (2-4)

Подставив в эти уравнения вместо t любое значение, можно найти положение точки в пространстве в соответствующий момент времени. Следовательно, уравнения (2.4) определяют движение точки относительно выбранной системы отсчета. Эти уравнения называются уравнениями движения точки в координатной форме. Функции (2.4) должны быть не­прерывными, однозначными и, как это будет показано ниже, дифференци­руемыми, по крайней мере, дважды.

Если точка совершает плоское движение, т.е. движется в одной плоскости, то, совместив с плоскостью ее движения одну из координатных плоскостей, например, плоскость х О у, мы обратим в тождество третье уравнение системы (2.4). Таким образом, плоское движение точки определяется двумя уравнениями этой системы. Прямолинейное движение точки определяется одним из этих уравнений, т.к. направив одну из координатных осей вдоль траектории точки, можно обратить в тождества два уравнения системы (2.4).

2.2.3. Естественный способ

Пусть некоторая точка, совершая движение по траектории KL (рис. 2.4) в момент t занимает положение М. Если точка М движется относительно выбранного тела отсчета, то траектория KL неизменно связана с этим телом. Будем считать, что траектория точки М нам задана. Возьмем на этой траектории неизменно связанную с ней точку А (а сле­довательно, и с телом отсчета).

Т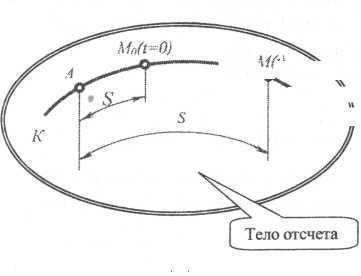 огда положение рассматриваемой точки М на ее траектории будет определено, если задана ее дуговая координата S, отсчитывается вдоль траектории от точки А, называемой началом дуговых координат. Ду­говая координата является величиной алгебраической. Она может быть по­ложительной или отрицательной в зависимости от того, с какой стороны от точки А расположена точка М. Правило знаков для дуговой координаты должно быть выбрано предварительно.

Не следует дуговую координату точки смешивать с длиной пройден­ного ей пути. Пройденный путь всегда положителен и при движении точки всегда возрастает, независимо от направления движения.

Дуговая координата S при движении точки, в общем случае, непре­рывно изменяется с течением времени. Она является непрерывной, однозначной и дважды дифференцируемой функ­цией времени, т.е. S= f (t). (2.5)

Уравнение такого вида определяет движение точки по ее траектории, т.к. подставив в него любое значение времени t, можно определить соответст­вующее алгебраическое значение дуговой координаты S и, таким образом, определяется положение точки на ее траектории в соответствующий момент времени. В этом случае системой отсчета является сама траектория вместе с началом А дуговых координат. Уравнение (2.5) называется уравнением движения точки по ее траектории или уравнением ее движения в естест­венной форме. Заметим, что это уравнение определяет движение точки только в том случае, если задана ее траектория, выбрано начало дуговых координат и правило знаков для дуговой координаты.

Положение М₀ занимаемой точкой М в начальный момент, называет­ся начальным ее положением. Дуговая координата S_o начального положе­ния точки называется начальной дуговой координатой. Она определяется из уравнения (2.5) подстановкой в него t = 0, т.е.

So =f(0). (2.6)