1.3. Система сходящихся сил.

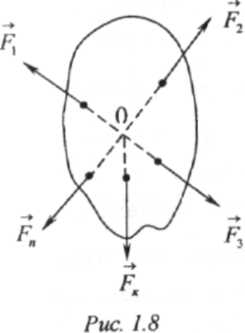
Ранее были рассмотрены аксиомы статики и их основные определения. Теперь перейдем к изу­чению простейшей системы сил. Такой системой является система сходящихся сил, т.е. таких сил, линии которых пересекаются в одной точке (рис. 1.8).Если линии действия всех сил такой системы расположены в одной плоскости, то система назы­вается плоской системой сходящихся сил. В про­тивном случае эта система называется простран­ственной системой сходящихся сил.

1.3.1. Приведение системы сходящихся сил к простейшему виду

а) Геометрический метод сложения сходящихся сил .

Термин "сложить систему сил" означает - найти её равнодействую­щую. Задачи о сложении и равновесии сходящих­ся сил впервые решены Вариньоном. Начнем решение с поставленной задачи со случая сложения двух сходящихся сил. Пусть в точках А и В (рис. 1.9) к твердому телу приложе­ны две силы F₁ и F₂, линии действия которых пе­ресекаются в точке О.

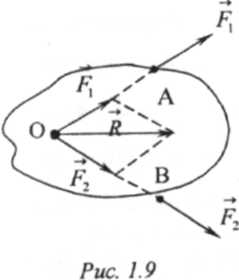
Поскольку сила является вектором скользящим, то перенося каждую из данных сил F₁и F₂ вдоль их действия в точку О, получим две силы, приложенные к твердому телу в одной точке О. Сложив их, на основании аксиомы 3, получим равнодействующую А, приложен­ную в этой точке и изображенную диагональю параллелограмма, постро­енного на этих силах, как на сторонах. Такой способ сложения двух схо­дящихся сил называется правилом параллелограмма сил.

Эта же задача также может быть решена с помощью правила треугольника сил, заключающего­ся в следующем (рис. 1.10). -

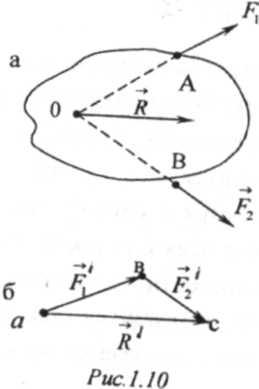
Из произвольной точки а (рис. 1.10б) проведем вектор f^/=f, и из конца его b вектор f₁=F₂. Соединив точку а с концом вектора f₂, получим вектор r', равный рав­нодействующей r данных сил. Последняя сила приложена в точке 0 пересечения линий действия данных сил f, и f₂.

Теперь допустим, что требуется сложить систему сходя­щихся сил f₁, f₂ f,₃ приложенных к твердому телу в различных его точках a₁, а₂, ...а_п (рис. 1.11).

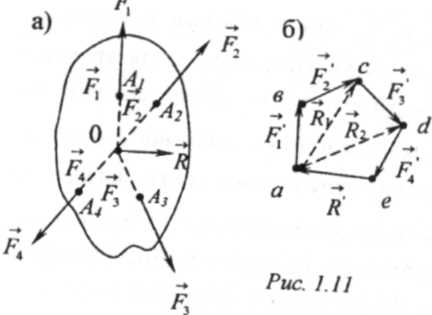
Перенеся все силы вдоль их линий действия в общую их точку пере­сечения, получим систему сил приложенных к данному телу в одной точке 0. Для сложения сил воспользуемся методом последовательного их сложе­ния.

Сложим сначала силы f₁ и f₂, использовав правило треугольника сил. Для этого из произвольной точки а (рис. 1.11б) проведем последовательно векторы F₁f₂ , равные соответственно векторам f₁ и f₂. Равнодействующая этих сил равна век­тору r', проведенному из точки а в конец с вектора f₂ , и приложена в точке 0 пересечения линий дей­ствия данных сил (рис. 1.11а), причем r, =F₁ +f₂ . На рис. 1.11 б вектор R, показан пунктиром. Теперь, найденную равнодействующую r, сложим со следующей силой f₃. Для этого из конца с вектора r₁ проведем вектор f₂ =f₃. Тогда вектор R₂ (см. пунктир на рис. 1.116), проведенный из точки а в конце d вектора F₃, будет равен равнодействующей сил R, и F₃, т.е. трех сил F ₁F₂, F₃, причем R ₂=R₁ +F₃,=F_t +F₂ +F₃. Приложена эта равнодействую­щая также в точке 0 (на рис. 1.11а) равнодействующие R₂ и R₁, не показа­ны. Аналогично складывая равнодействующую R₂ последовательно со всеми остальными силами данной системы, получим равнодействующую r всех данных сил, приложенную в точке 0 и равную r = R^/ =F₁+F₂'+F₃'+...+ F_п' =ΣF_к,

где R' - вектор, проведенный из точки а в конец е последнего из векторов, построенных на рис. 1.116.

Учтя, что F_k=F_k (к=1,2,...п), окончательно получим r = ΣF_к. .

Сумма, стоящая в правой части этого равенства, называется векторной суммой сил.

Как нетрудно видеть, для построения вектора r равнодействующей системы сходящихся сил достаточно, начиная от произвольной точки а провести последовательно один за другим векторы f₁,f₂,...,f_п, равные со­ответственно векторам данной системы сил F, ,F₂ ,.. f_п, из точки а про­вести вектор r в конец е последнего из проведенных векторов и затем перенести его параллельно в точку 0 пересечения линий действия данных сил. Многоугольник abcde называется многоугольником сил, а такой способ сложения системы сходящихся сил получил название правила многоуголь­ника. Вектор r , направленный противоположно всем остальным сторо­нам многоугольника adcde при обходе его периметра, называется замы­кающей стороной многоугольника сил.

Таким образом, равнодействующая системы сходящихся сил равна замыкающей стороне многоугольника сил, построенного на данных силах, как на сторонах, или векторной сумме этих сил, и приложена в точке пере­сечения их линий действия.

Заметим, что описанный способ применим не только для сложения плоской системы сходящихся сил. Им можно также пользоваться и при сложении сходящихся сил, не лежащих в одной плоскости, хотя в послед­нем случае применение его очень неудобно, так как трудно изобразить на плоскости пространственный многоугольник сил.

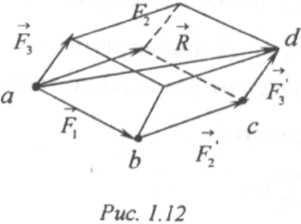
Особого внимания заслуживает сложение трех сходящихся сил, ли­нии действия которых не лежат в одной плоскости. Пусть дана пространственная система трех сходящихся сил F₁, F₂, F₃, (рис. 1.12). Построим на этих силах пространственный многоугольник сил abсd (точка а этого многоугольника совмещена с точкой приложения сил данной системы).

Его замыкающая сторона ad = R равна по величине и направлению равнодействующей данных сил. Достроив этот многоугольник до параллелограмма, как это показано на рисунке, убедим­ся, что вектор равнодействующей R изображается его диагональю, а векторы данных сил F₁, F₂ и F₃ - ребрами, исходящими из той же верши­ны d, из которой проведен вектор r .

Таким образом, приходим к выводу, что равнодействующая трех сходящихся сил, линии действия которых не лежат в одной плоскости, изображается диагональю параллелепипеда, по­строенного на данных силах, как на ребрах, исходящих из общей вершины.

б) Векторное условие равновесия системы сходящихся сил

Пусть r - равнодействующая системы сходящихся сил F₁, F₂, ..,F_п-1, (рис. 1.13).

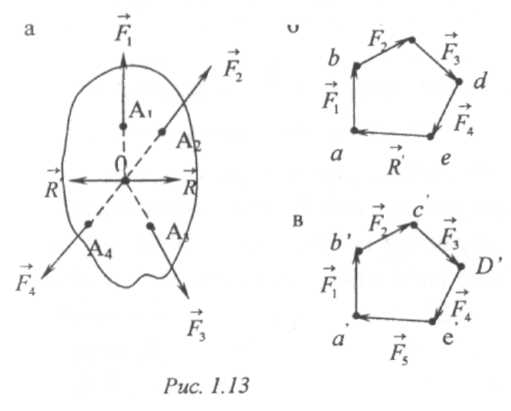
Поскольку сила R ', равная по модулю равнодействующей R и направленная по той же прямой в противоположную сторону, уравновешивает данную систему сил, то, присоединив к данной системе сил F_п = r (на рис. 1.13 силу F₅) , мы получим взаимно уравновешенную систему сил F₁, F₂ , .., F_п (на рис. 1.13 систему F₁ F₂, .., F_п).

Если теперь вектор F_n присоединить к ломаной кривой abсde, то конец его совпадает с началом а вектора первой силы F, (рис. 1.1 Зв). Многоугольник сил abсdea, стороны которого направлены при обходе вдоль его периметра в одном и том же направлении, называется замкнутым. Равнодействующая такой системы сил равна нулю.

Следовательно, если система сходящихся сил вза­имно уравновешивается, то соответствующий много­угольник сил замкнут и рав­нодействующая или вектор­ная сумма сил равна 0.

Таким образом, необходимым усло­вием равновесия системы сходящихся сил является равенство 0 векторной суммы данных сил. Это условие является также и достаточным.

В самом деле, если дана система сходящихся сил F₁, F₂, .., F_п, век­торная сумма которых равна нулю (рис. 1.13в), то, заменив силы F,, F₂, .., F_п-1 , их равнодействующей

R= -F_п приложенной в точке 0 (рис. 1.13а), будем иметь две равные и противоположно направленные по одной пря­мой силы R и r =F„, которые, на основании аксиомы 2, взаимно урав­новешиваются. Следовательно, уравновешивается и система сил F₁, F₂, .., F_п.

Та­ким образом, векторным условием равновесия системы сходящихся сил является векторное равенство: ΣF_t=0, что означает, что многоугольник сил, построенный на силах данной систе­мы, должен быть замкнутым.

в) Разложение силы на составляющие, приложенные в её точке приложения

Теперь решим обратную задачу. Пусть задана сила¯F, приложенная в некоторой точке А. Требуется разложить её на составляющие, приложен­ные в этой же точке.

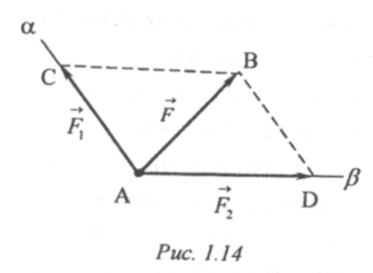
Рассмотрим сначала случай разложения силы F на две составляю­щие F₁ и F₂ (рис. 1.14). Эта задача сводится к построению параллелограм­ма, диагональю которого изображался бы вектор данной силы. Таких паралле­лограммов можно построить бесчислен­ное множество. Следовательно, постав­ленная задача является многозначной. Чтобы сделать её

однозначной, необхо­димо задать дополнительные условия. Наиболее часто встречается задача о разложении силы на две составляющие, приложенные в её точке приложения, по заданным линиям действия иско­мых составляющих.

Пусть силу ¯F, приложенную в точке А (рис. 1.14), требуется разло­жить на две составляющие, приложенные в этой же точке и направленные по заданным прямым Аа и Аβ. Для решения этой задачи достаточно из конца В вектора F провести прямые ВД и ВС, параллельные соответст­венно прямым Аа и Аβ Тогда стороны АС и AD построенного таким обра­зом параллелограмма ABCD изобразят векторы искомых составляющих F₁ и F₂.

Для разложения силы на две составляющие, приложенные в её точке приложения, могут быть также заданы величины составляющих сил или величина и линия действия одной из них и, наконец, величина одной и ли­ния другой. Во всех этих случаях задача решается путем геометрического построения параллелограмма сил. Предлагается самостоятельно рассмот­реть все эти случаи и выяснить, при каких условиях каждая из этих задач является однозначной, двузначной или не имеет решений.

Рассмотрим теперь случай разложения силы на три некомпланарные составляющие, приложенные в её же точке приложения. Эта задача сво­дится к построению параллелепипеда, диагональю которого изображался бы вектор данной силы, и в общем случае также является многозначной. Для того чтобы сделать её однозначной, необходимо задать дополнитель­ные условия. Наиболее важным является случай разложения силы на три некомпланарные составляющие, приложенные в одной с ней точке, по за­данным линиям действия всех трех составляющих.

Пусть требуется разложить силу F, (рис. 1.15), приложенную в точке А, на три составляющие, приложенные в этой же точке и направленные по з аданным прямым Аа, Аβ и Ау, не лежащие в одной плоскости. Для решения этой задачи следует через конец β вектора силы F про­вести три плоскости ВКСМ, BMDN, BKEN, параллельные соответственно плоскостям βАγ, аАγ и аАβ, которые пересекут заданные прямые соответственно в точках С, D и Е. То­гда ребра AC, AD и АЕ построенного таким образом параллепипеда изобразят векторы.

искомых составляющих F₁, F₂, F₃,