Лекція №4.Особливі точки. Особливі рішення. Рівняння Клеро

1. Особливі точки. Особливі рішення.

Означення. Точка називається особливою точкою для даного диференціального рівняння, якщо, або не існує рішення, що проходить через дану точку, або через дану точку проходить кілька рішень.

Точка може бути особливою для рівняння y′=f (х, у) якщо у цієї точки не виконуються умови теореми існування та єдиності рішення. Наприклад f (х, у) у точці терпе розрив.

Приклади.

1) y′= , (0;0) – особлива точка, оскільки f (х, у)= в точці (0,0) терпе розрив. Розв’язуючи рівняння отримаємо , і ln|y|=2ln|x|+lnc. Отже загальний розв’язок має вигляд y=cx . Таким чином через точку (0,0) проходить нескінченно багато рішень(параболи). Точку такого типу називають вузол.

2) y′= ( (0;0) – особлива точка). Розв’язуючи рівняння отримаємо , і ln|y|=ln , отже y= . Тобто через точку (0,0) не проходить ні один розв’язок (гіпербола). Таку точку називають сідло.

3) y′= ( (0;0) – особлива точка). Розв’язуючи отримаємо загальний розв’язок: уdy=-хdx, dy=- хdх , отже y =-x +с або y + x =с. Через точку (0,0) не проходить ні один розв’язок (коло). Таку точку називають центр.

4) y′= ( (0;0) – особлива точка). Загальний розв’язок однорідного рівняння має вигляд x²+y²=с або у полярних координатах =с _. Через точку (0,0) теж не проходить ні один розв’язок (спіраль). Таку точку називають фокус.

Самостійно привести зображення кожної з вказаних ситуацій.

Друга умова з порушенням якою зв’язані особливі точки це умова Ліпшица, або обмеженість , тобто особливі точки можуть з’явитися у точках при наближені до яких необмежено росте, або в котрих виконується рівність .

Означення. Крива називається особою, якщо всі точки кривої є особливими. Якщо особлива крива є рішенням диференціального рівняння, вона називається особливим рішенням.

Приклад. Розглянемо рівняння y′= +1. Оскільки то 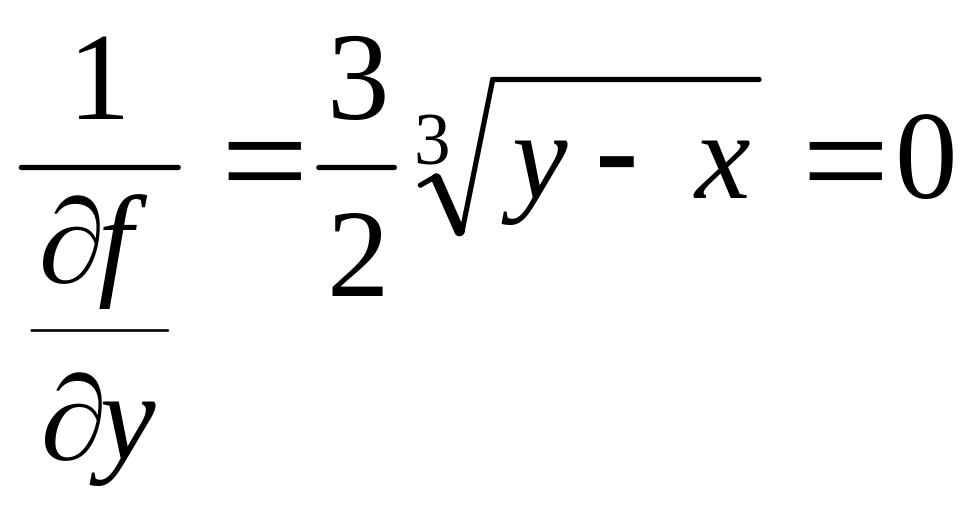виконується для точок, що задовольняють рівності у=х – особливе рішення. Той факт, у=х рішення нескладно отримати підставляючи у=х до рівняння.

Знайдемо загальне рішення даного рівняння. Для цього введемо заміну z=y – х, z′=y′ - 1 і y′= z′+1, отже z′+1= +1. Розв’язуючи останнє рівняння отримаємо =dx, =∫dx, тобто 3 =x+c, або = x +c і на кінець z= ( x +c) ³. Загальний розв’язок рівняння має вигляд y=x+ ( x +c) ³. Кожна крива цього сімейства проходить через точку кривої у=х і навпаки через кожну точку ( ) кривої у=х проходить деяка крива сімейства, при відповідному (самостійно зробити зображення сімейства та у=х), отже особливий розв’язок рівняння.

2. Огибаюча сімейства кривих. Рівняння Клеро.

Означення. Нехай F(x,y,c)=0 сімейство кривих. Тоді L називається огибаючою цього сімейства якщо в кожній своїй точці вона дотикається лінії сімейства і кожна крива сімейства дотикається до L.

Якщо F(x,y,c)=0 є загальним рішенням диференціального рівняння , то тоді огибаюча сімейства теж є рішенням даного рівняння. Оскільки дотична до огибаючої у довільній точці збігається з дотичною, проведеною до кривої даного сімейства, що дотикається огибаючої у даній точці, то дотична до огибаючої збігається з напрямком, що задається диференціальним рівнянням у даній точці. Отже огибаюча є інтегральною кривою, тобто рішенням. Оскільки через будь-яку точку огибаючої проходить два рішення (огибаюча та деяке рішення з сімейства), то огибаюча – особливе рішення.

Якщо F(x,y,c)=0 сімейство, то огибаючу його визначають з системи: .

Приклад. Для рівняння загальне рішення має вигляд y=x+ .

Знайдемо огибаючу до загального рішення з системи: , , отже у=х .

у=х - огибаюча загального рішення рівняння, отже є особливим рішенням.

Означення. Рівняння виду y=xy′+ (у′) називається рівнянням Клеро.

Знайдемо загальний розв’язок та особливий розв’язок рівняння Клеро. Розглянемо заміну у′=p, тоді y=xp+ (p) і у′=p+xp′+p′ ′(p), враховуючи заміну отримаємо p=p+xp′+p′ ′(p) або

p′ (x+ ′ (p)) =0. Остання рівність виконується у двох випадках:

1) p′=0, тобто p=c і загальний розв’язок має вид y=cx+ (c);

2) , тобто рішення є огибаюча загального розв’язка , яку знаходимо з системи .

Приклад. Знайти загальне та особливе рішення рівняння y=xy′+ (у′) . Загальний розв’язок має вигляд y=cx+ c . Огибаючу знаходимо з системи . Отже c= і y= + або y= . Самостійно розглянути рівняння Лагранжа.