Практичне заняття №9. Типи рівнянь другого порядку у частинних похідних. Рівняння коливання струни. Формула Даламбера

Необхідні відомості: 1. Означення рівняння другого порядку у частинних похідних. Типи рівнянь.

2. Формула Даламбера.

Задачі.

Привести до канонічного виду

1.1

1.2 . Спростити рівняння з постійними коефіцієнтами.

2.1 Знайти розв’язок

2.2 Знайти форму струни, визначеною рівнянням у момент , якщо

2.3 Знайти форму струни, визначеною рівнянням ,

якщо ,

у момент

2.4 Знайти відхилення точки х=1 струни ( ) у довільний момент часу від положення спокою, якщо у момент струна знаходилась у спокої, а точка х=0 рухається за законом .

Задачі для самостійної роботи.

Привести до канонічного виду

1. . 2. . 3. .

4. .

5. .

Знайти розв’язок

6. .

7. .

8. Знайти форму струни, визначеною рівнянням .

9. Розв’язати задачу 2.4 при умові .

10. Розв’язати рівняння

.

11. Розв’язати рівняння

.

12. Розв’язати рівняння

.

13. Розв’язати рівняння

.

Лекція №13. Неоднорідні гіперболічні, рівняння на прямій і піввісі. Метод Фур’є розділення змінних

1. Неоднорідні гіперболічні рівняння на прямій і піввісі.

Розглянемо задачу Коши

.

Використовуючи формулу Даламбера (дивіться докладно[5]), нескладно отримати розв’язок неоднорідного рівняння, що задовольняє нульовим початковим умовам, у вигляді:

.

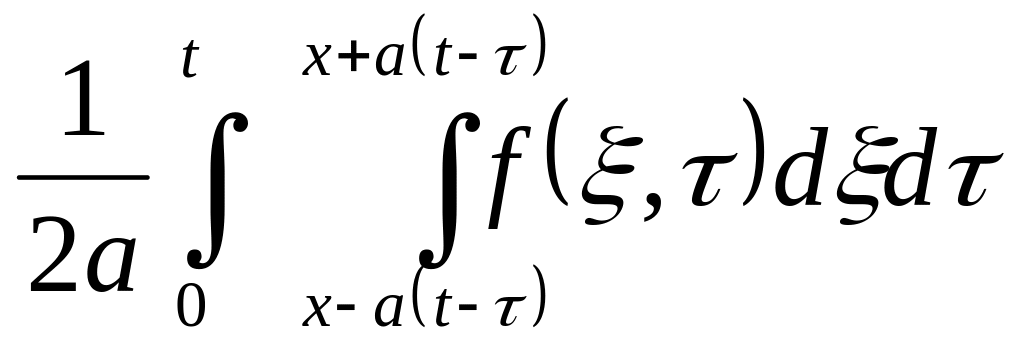Тоді розв’язок вихідної задачі має вид:

.

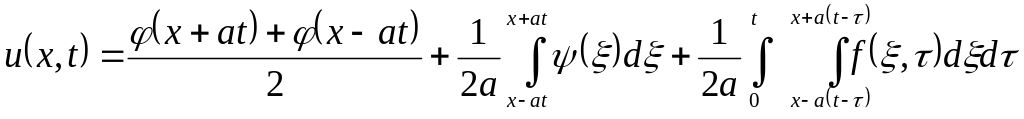У випадку задачі

,

враховуючи все вищевказане, отримаємо

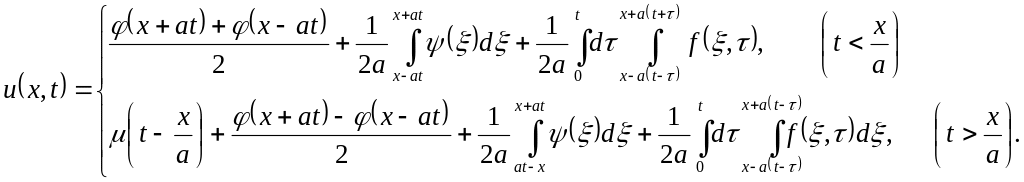
Із отриманих формул випливає існування і однозначність розв’язку задач.

2. Метод розділення змінних.

Розглянемо задачу для скінченої струни.

Спочатку знайдемо розв’язок наступної крайової задачі

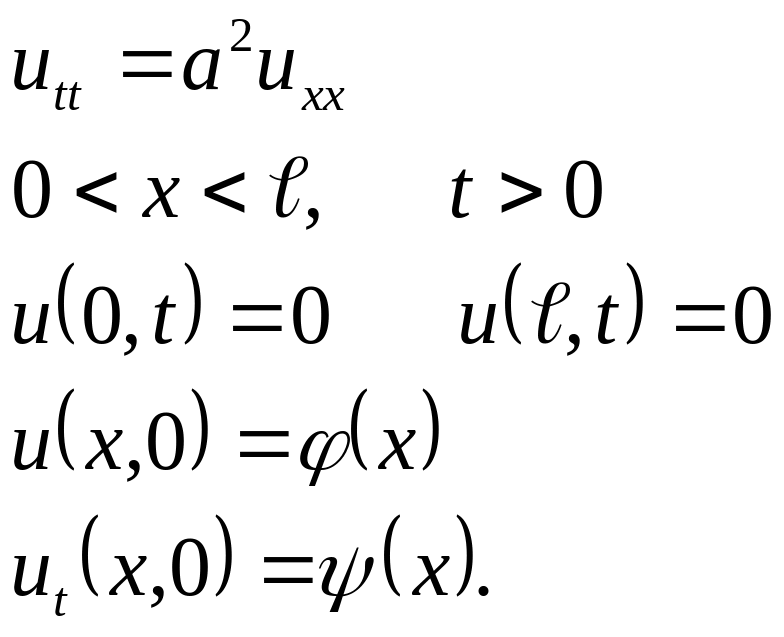
Розв’яжемо допоміжну задачу: знайти розв’язок такий, що ,

і постає у вигляді .

Підставивши у рівняння отримаємо

або

Для і Т отримаємо звичайні диференційні рівняння:

Граничні умови дають Звідки .

Таким чином, для знаходження треба розв’язати задачу про власні значення.

Знайти ті , при яких існує розв’язок задачі:

Сформульована задача називається задачею Штурма-Лиувилля.

1. При

, тобто і , отже .

2. При

1. При

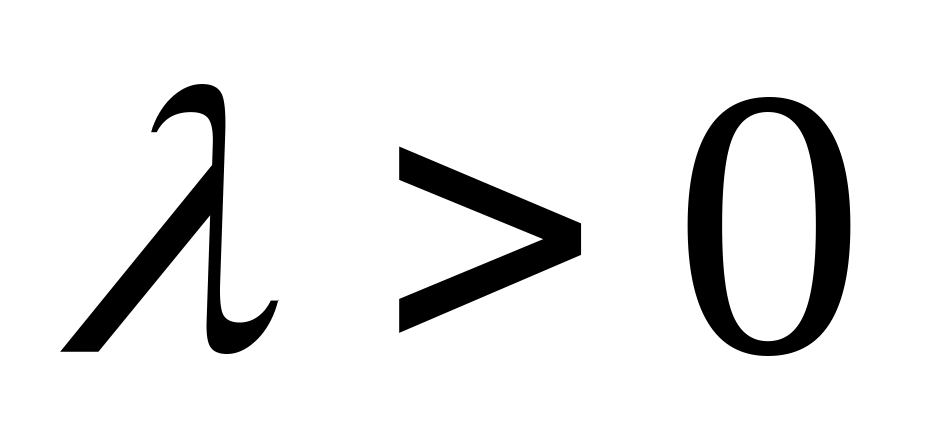
тобто нетривіальний розв’язок можливий при . Отже при де А_п – довільна константа.

Цим же значенням відповідає розв’язок рівняння

, де - довільні коефіцієнти.

Тоді, повертаючись до початкової здачі отримаємо, що функція

- частинні розв’язки рівняння, що задовольняють нульвим граничним умовам.

Для знаходження розв’язку початкової крайової задачі зазначимо, що в силу лінійності рівняння, - задовольняє рівнянню і нульовим граничним умовам, отже

. Знайдемо і враховуючи початкові умови.

, тобто

.

Зауваження 1. Звісно є розв’язком коли відповідні ряди для збігаються. В силу властивостей коефіцієнтів Фур’є всі ряди (для ) у загальному випадку сходяться, якщо має частково-неперервну похідну 3-го порядку, а має частково-неперервну похідну 2-го порядку і і значить – коректно визначений розв’язок, що задовольняє теорему єдиності.

Зауваження 2. - власні частоти коливань струни, або оскільки то (Т – величина натягу, - щільність струни).

- основний тон, решта - обертони. Приведені формули визначають частоту і, відповідно, період основного коливання, пояснюють наступні закони коливання струни, відкриті вперше експериментально (Мерсен)

1. Для струн однакової щільності і однакового натягу період коливання струни пропорційно її довжині.

2. При заданій довжині період змінюється обернено пропорційно кореню квадратному з натягу.

3. При заданій довжині і натягу період змінюється пропорційно кореню квадратному з щільності.

Більш детально про додатки до теорії звуку дивіться [5].