Практичне заняття №2. Однорідні рівняння

Необхідні відомості: 1. Означення однорідного рівняння та його розвязок.

2. Рівняння, що приводяться до однорідних.

Задачі.

1. Знайти загальні рішення рівнянь.

1) ху′-y=

2) y′= +

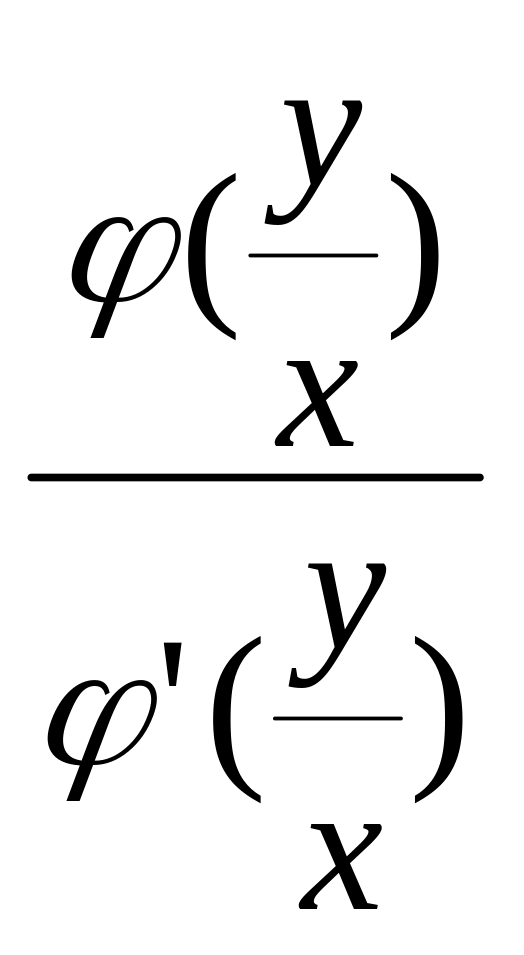
2. Знайти приватне рішення диференціального рівняння, що задовольняє даним початковим умовам.

(y²-3x²)dy+2xydx=0; y| =1

3. Привести рівняння y′= + φ( ) до квадратури. Яка повинна бути функція φ( ), щоб загальним рішенням даного рівняння було y= ?

4. Знайти лінію, у якої квадрат довжини відрізка, що відтинається будь-якій дотичній від осі ординат, дорівнює добутку координат точки торкання.

5. Знайти лінію, у якої довжина полярного радіуса будь-якої її точки М рівняється відстані між точкою перетинання дотичній у точці М с віссю Оу й початком координат.

6. Розв’язати за допомогою заміни:

1. , 2. .

Задачі для самостійної роботи.

Знайти загальні рішення рівнянь.

1. y′= - 2

2.y′=

3. xdx - ydx=ydy

4. y′=

5. y′= +

6. y + x y′=xyy′

7. y′= +

8. xy′=yln

9. (3y +3xy+x ) dx=(x +2xy) dy

Знайти приватні рішення диференціальних рівнянь, що задовольняють даним початковим умовам.

10.(xy′-y) arctg ( ) =x; y| =0

11. y′= ; y| = - 1

12.y + 2x – y=0; y| =

13. Якою поверхнею обертання є дзеркало прожектора, якщо промені світла, що виходять із точечного джерела, відбившись, направляються паралельним пучком?

Знайти розв’язки за допомогою зміни змінної.

14. 15.

Лекція №3. Лінійні рівняння першого порядку. Рівняння Бернуллі та Рікатті-Буля

1. Лінійні рівняння першого порядку.

Означення. Рівняння виду y′=а(х)у+b(х) називається лінійним рівнянням першого порядку.

Теорема. Нехай а(х), b(х) неперервні на [a, b], тоді задача Коші в будь-якій точці смуги [a,b] має єдине рішення.

Доведення теореми випливає з загальної теореми існування та єдиності розв’язку задачі Коші, оскільки f(x,y)=а(х)у+b(х) неперервна на області [a,b] , а обмежена (а(х) – неперервна на [a, b]).

Знайдемо рішення рівняння методом невизначених коефіцієнтів. Спочатку вирішимо однорідне рівняння y′=а(х)у, або =a(x)dx. Інтегруючи, будемо мати . Отже ln|y|=∫a(x) dx+lnc, c>0, або y=c _. Рішення лінійного рівняння будемо шукати у вигляді y=c(х) , де c(х) – невідома функція.

Оскільки y=c (х) , то y′= c (х) +c(x) a(x) . Підставляючи y та y′ у рівняння y′=а(х)у+b(х) будемо мати c′ (х) +c(x) a(x) =a(x) c(x) + b (х). Отже c′ (х) = b (х) , або с (х)= ∫ b(х) dx. Таким чином отримаємо розв’язок рівняння у вигляді y(x) = (∫ b (х) dx)∙ _.

Приклад. Розв’язати y′=xy+x .

Оскільки а(х)=х, а b(х)= x² маємо y=(∫ x²∙ dx)∙ =(∫ x²∙ dx)∙ _.