3. Устойчивость оптимального решения злп:

a) Изменение свободных членов системы ограничений.

Алгоритм:

1) Найти новые значения базисных переменных в последней итерации исходной задачи по формуле (4.3) и минимальное значение целевой функции по формуле (4.6).

2) Если , то комбинация базисных переменных остается прежней, симплекс-множители не меняются; если , то двойственным симплекс-методом продолжить решение и найти новую комбинацию базисных переменных и их значения, а также симплекс-множители и значение целевой функции.

3) Записать ответ.

Пример 1. Предположим, что изменилось количество имеющегося сырья на кондитерской фабрике . Рассмотрим, как изменится при этом решении задачи.

Найдем новое базисное решение по формуле (4.3):

.

Так как среди полученных нет отрицательных, то текущие базисные переменные x₁, x₅, x₃ с новыми значениями составляют допустимое решение. Соответствующее этому решению оптимальное значение целевой функции равно .

Ответ: x* = (1; 6; 16), = 280, то есть доход фабрики увеличится по сравнению с прежним.

Пример 2. Пусть изменилось количество имеющегося сырья = . Рассмотрим, как изменится при этом решении задачи.

Найдем новое базисное решение и значение целевой функции по формулам (4.3) и (4.6):

= ,

.

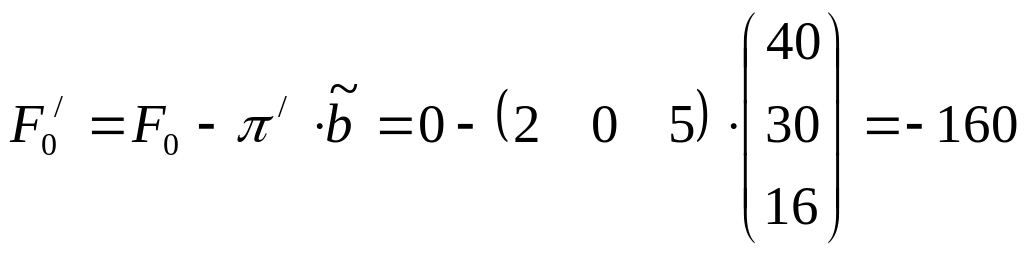Полученное решение не является допустимым, поскольку теперь x₁ =-14. Заменим значения в столбце свободных коэффициентов оптимальной симплекс-таблицы исходной задачи на полученные и для возврата в ОДР применим двойственный симплекс-метод:

	б.п.
2	x1*	1	-1/4	0	1/4	0	-3/2	-14
	x5	0	5/2	0	-3/2	1	6	66
	x3	0	1	1	0	0	1	16
	F	0	3	0	2	0	5*	-160
3	x6	-2/3	1/6	0	-1/6	0	1	28/3
	x5			0		1	0	10
	x3			1		0	0	20/3
	F	10/3	13/6	0	17/16	0	0	-340/3

Ответ: x* = (0; 0; 20/3); = 340/3, то есть доход фабрики уменьшится по сравнению с прежним.

б) Включение дополнительных переменных.

Алгоритм:

1) Найти в последней итерации исходной задачи новый столбец и по формулам (4.2) и (4.4).

2) Если , то план и значение целевой функции не изменяются, следовательно, в базис не включается.

3) Если , то следует продолжить решение основным симплекс-методом, включив в базис симплекс-таблицы; найти новый базис, план x*, значение целевой функции F*.

4) Записать ответ.

Пример 3. Кондитерская фабрика в дополнение к имеющимся видам карамели планирует производить карамель четвертого вида x₇, при этом расход сырья каждого вида задан матрицей p₇ = , доход от реализации единицы этой продукции c₇ = 20. Как изменится доход фабрики по сравнению с первоначальным?

Вычислим столбец коэффициентов ограничений, соответствующий переменной x₇ по формулам (4.2) и (4.4):

· = ,

· .

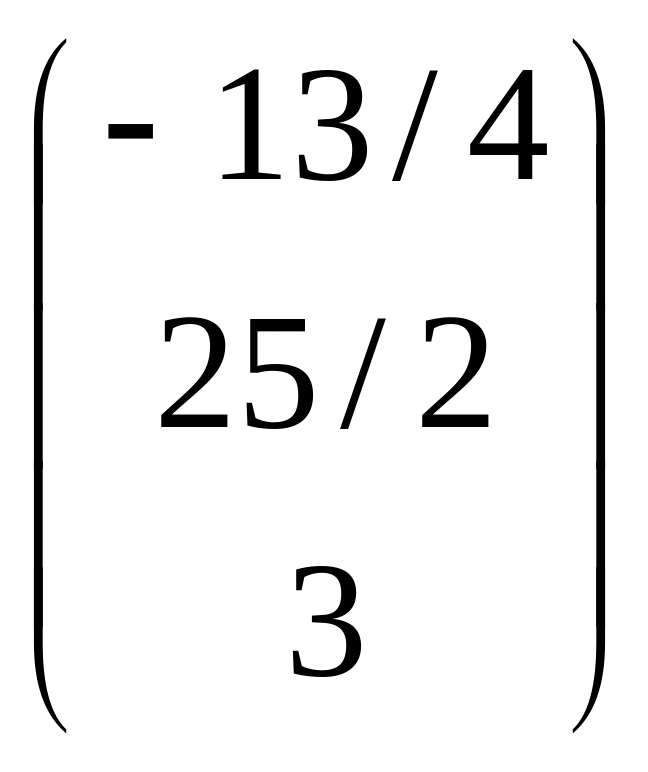Так как , то план и значение целевой функции не изменяются.

Ответ: x* = (2; 0; 12), = 220.

Пример 4. Кондитерская фабрика в дополнение к имеющимся видам карамели планирует производить карамель четвертого вида x₈, при этом расход сырья каждого вида задан матрицей p₈ = , доход от реализации единицы этой продукции c₈ = 15. Как изменится доход фабрики по сравнению с первоначальным?

Вычислим столбец коэффициентов ограничений, соответствующий переменной x₇ по формулам (4.2) и (4.4):

= ,

· .

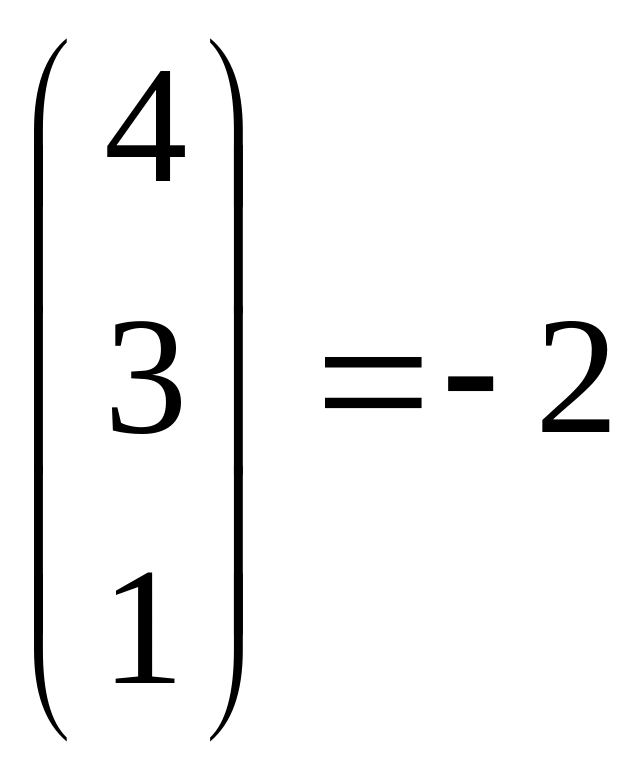Поскольку , то следует продолжить решение задачи основным симплекс-методом, включив в оптимальную симплекс-таблицу исходной задачи:

	б.п.
2	x1	1	-1/4	0	1/4	0	-3/2	-1/2	2
	x5*	0	5/2	0	-3/2	1	6	3	12
	x3	0	1	1	0	0	1	1	12
	F	0	3	0	2	0	5	-2*	-220
3	x1	1		0				0	4
	x8	0	5/6	0	-1/2	1/3	2	1	4
	x3	0		1				0	8
	F	0	14/3	0	1	2/3	9	0	-228

Ответ: x* = (4;0;8;4); = 228, то есть доход фабрики увеличится по сравнению с прежним.

в) Изменение значений коэффициентов целевой функции.

Алгоритм:

1) Записать новые коэффициенты с учетом ориентации целевой функции на минимум.

2) Найти новые коэффициенты в последней итерации симплекс-таблицы по формуле (4.5).

3) Если при неискусственных переменных, то комбинация базисных переменных и их оптимальные значения не изменяются. Найти значение целевой функции по формуле (4.6).

4) Если при неискусственных переменных, то следует выписать симплекс-множители и найти по формуле (4.6), затем продолжить решение основным симплекс-методом.

5) Записать ответ.

Пример 5. Кондитерская фабрика проводит новую ценовую политику относительно реализации карамели. В соответствии с этим целевая функция задачи принимает вид . Как изменится решение задачи?

Запишем новые коэффициенты с учетом ориентации целевой функции на минимум , , , = = .

Найдем новые коэффициенты в последней итерации симплекс-таблицы по формуле (4.5):

,

.

Следовательно, симплекс-множители в данном случае имеют вид .

Найдем значение целевой функции по формуле (4.6):

.

Так как , то план оптимален.

Ответ: x* = (2;0;12), = 392, то есть доход фабрики увеличится по сравнению с прежним.

Пример 6. Кондитерская фабрика проводит новую ценовую политику относительно реализации карамели. В соответствии с этим целевая функция задачи принимает вид . Как изменится решение задачи?

Запишем новые коэффициенты с учетом ориентации целевой функции на минимум , , , = = .

Найдем новые коэффициенты в последней итерации симплекс-таблицы по формуле (4.5):

, .

Следовательно, симплекс-множители в данном случае имеют вид .

Значение целевой функции .

Так как , то следует продолжить решение задачи основным симплекс-методом, изменив коэффициенты строки целевой функции оптимальной симплекс-таблицы решения исходной задачи:

	б.п.
2	x1	1	-1/4	0	1/4	0	-3/2	2
	x5*	0	5/2	0	-3/2	1	6	12
	x3	0	1	1	0	0	1	12
	F	0	-5*	0	3	0	0	-240
3	x1	1	0	0				16/5
	x2	0	1	0	-3/5	2/5	12/5	24/5
	x3	0	0	1				36/5
	F	0	0	0	0	2	12	-264

Ответ: x* = (16/5;24/5;36/5), = 264, то есть доход фабрики увеличится по сравнению с прежним.

г) Включение дополнительных ограничений.

Алгоритм:

1) Подставить оптимальный план исходной задачи в новое ограничение.

2) Если соотношение ограничения выполняется, то план и значение целевой функции не меняются, ответ идентичен ответу исходной задачи.

3) Если соотношение ограничения не выполняется, то записать новое ограничение в канонической форме с предпочтительными переменными.

4) Преобразовать уравнение ограничения, исключив базисные переменные оптимальной таблицы исходной задачи, воспользовавшись соответствующими уравнениями этой таблицы.

5) Включить полученное уравнение в оптимальную таблицу исходной задачи с учетом новой базисной переменной .

6) Продолжить решение двойственным симплекс-методом и записать ответ.

Пример 7. Предположим, что кондитерская фабрика изменила состав выпускаемой карамели, и теперь для производства карамели необходим четвертый вид сырья. Этот тип сырья требуется при производстве третьего вида карамели, количество данного вида сырья на фабрике составляет 8 усл. ед. В результате получаем новое ограничение . Как изменится прибыль фабрики по сравнению с первоначальной?

Данное ограничение не является избыточным, поскольку оно не удовлетворяется при текущем оптимальном решении. Необходимо ввести новое ограничение в оптимальную симплекс-таблицу исходной задачи и продолжить решение двойственным симплекс-методом. Запишем новое ограничение в канонической форме с предпочтительными переменными . Преобразуем уравнение ограничения, исключив базисную переменную x₃ оптимальной таблицы исходной задачи, воспользовавшись третьим уравнением этой таблицы:

Вычитая из первого уравнения второе, получим: .

Включим полученное уравнение в оптимальную таблицу исходной задачи с учетом новой базисной переменной и продолжим решение двойственным симплекс-методом:

	б.п.
2	x1	1	-1/4	0	1/4	0	-3/2	0	2
	x5	0	5/2	0	-3/2	1	6	0	12
	x3	0	1	1	0	0	1	0	12
	x7*	0	-1	0	0	0	-1	1	-4
	F	0	3*	0	2	0	5	0	-220
3	x1	1	0	0	1/4	0			3
	x5	0	0	0	-3/2	1			2
	x3	0	0	1	0	0			8
	x2	0	1	0	0	0	1	-1	4
	F	0	0	0	2	0	2	3	-208

Ответ: x* = (3;4;8), = 208, то есть прибыль фабрики уменьшилась.

Пример 8. Предположим, что кондитерская фабрика изменила состав выпускаемой карамели, и теперь для производства карамели необходим четвертый вид сырья. Этот тип сырья требуется при производстве второго вида карамели, количество данного вида сырья на фабрике составляет 2 усл. ед., причем оно должно быть использовано полностью. В результате получаем новое ограничение . Как изменится прибыль фабрики по сравнению с первоначальной?

Представим данное ограничение в виде системы двух неравенств:

Запишем новые ограничения в канонической форме с предпочтительными переменными

Включим полученные уравнения в оптимальную таблицу исходной задачи с учетом новых базисных переменных x₇ и x₈ и продолжим решение двойственным симплекс-методом:

	б.п.
2	x1	1	-1/4	0	1/4	0	-3/2	0	0	2
	x5	0	5/2	0	-3/2	1	6	0	0	12
	x3	0	1	1	0	0	1	0	0	12
	x7	0	1	0	0	0	0	1	0	2
	x8*	0	-1	0	0	0	0	0	1	-2
	F	0	3*	0	2	0	5	0	0	-220
3	x1	1	0	0	1/4	0	-3/2	0		5/2
	x5	0	0	0	-3/2	1	6	0		7
	x3	0	0	1	0	0	1	0		10
	x7	0	0	0	0	0	0	1		0
	x2	0	1	0	0	0	0	0	-1	2
	F	0	0	0	2	0	5	0	3	-214

Ответ: x* = (5/2;2;10), = 214, то есть прибыль фабрики уменьшилась.

Педагогический комментарий. Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение выявлять проблемы экономического характера при анализе конкретных ситуаций, предлагать способы их решения и оценивать ожидаемые результаты; умение разрабатывать и обосновывать варианты эффективных производственно-технологических решений; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение совершенствовать составление оперативно-производственного плана с использованием инструментария математического программирования; умение эффективно управлять экономическими процессами и регулировать использование комплекса имеющихся ресурсов; умение анализировать оптимальное решение ЗЛП на устойчивость и вариативность.