4.3 Критический диаметр изоляции

Для уменьшения потерь теплоты трубопроводами, колоннами, теплообменными аппаратами и другими аппаратами цилиндрической формы необходимо правильно выбрать материал тепловой изоляции. Запишем выражение для полного термического сопротивления стенки и проанализируем графически влияние внешнего диаметра на его величину.

.

При заданных , , и термическое сопротивление будет зависеть от наружного диаметра . Термическое сопротивление теплоотдачи . Термическое сопротивление теплопроводности с увеличением диаметра увеличивается. Термическое сопротивление теплоотдачи с наружной стороны цилиндра с увеличением уменьшается .

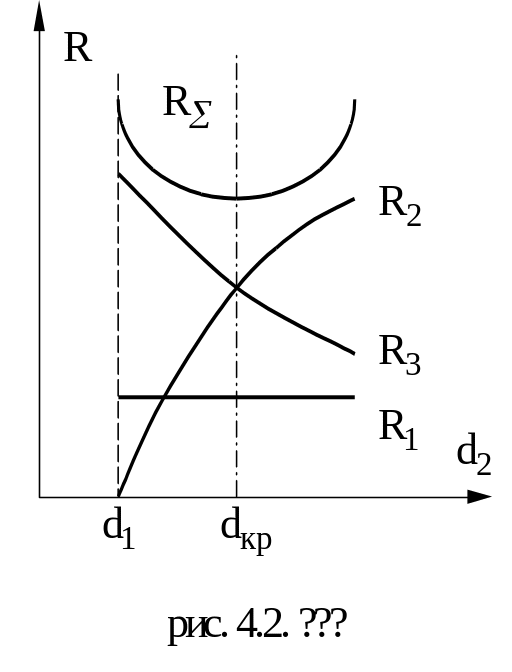
Анализ графика показывает, что в некоторой точке, где имеет место минимум суммарное термическое сопротивление, эта точка соответствует критическому диаметру для данного цилиндра (трубопровода) . В этом месте термическое сопротивление минимально. Чтобы исследовать кривую на минимум, необходимо продифференцировать . Приравняв к нулю первую производную и исследовав на минимумы и максимумы, мы получаем выражение для определения критического диаметра (это значение внешнего диаметра трубы, соответствующего минимальному полному термическому сопротивлению теплопередачи)

. (4.14)

Если , то в этом случае термическое сопротивление с увеличением диаметра уменьшается, а, следовательно, линейная плотность теплового потока через цилиндрическую поверхность увеличивается. Если , то с увеличением диаметра суммарное термическое сопротивление увеличивается, и линейная плотность теплового потока уменьшается (рис. 4.3).

.

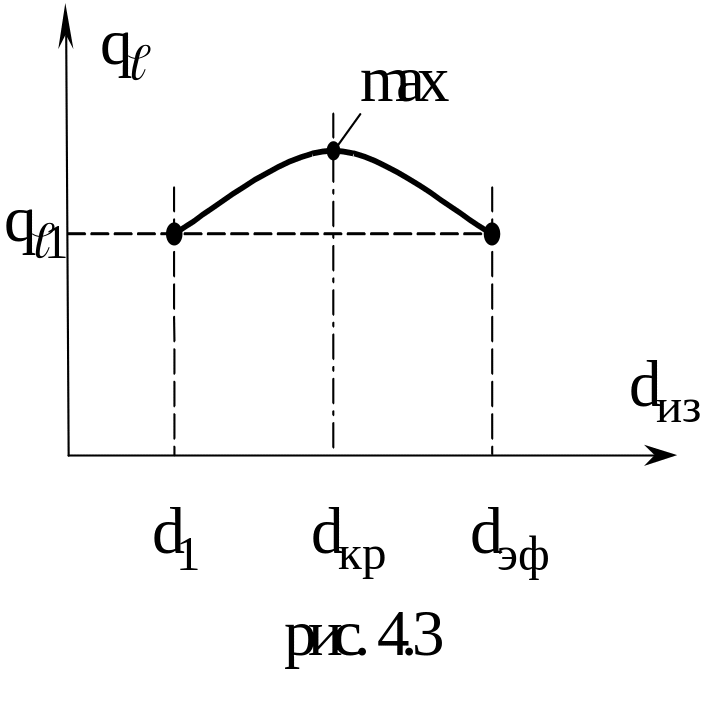
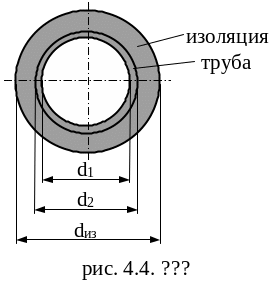
Если трубопровод изолирован, то наружный диаметр изоляции равен , и линейная плотность теплового потока равна . При толщине изоляции линейная плотность теплового потока тоже равна . Для правильного выбора материала тепловой изоляции критический диаметр изоляции должен быть

,

где – наружный диаметр трубы.

Если это условие не выполняется, то необходимо выбрать материал тепловой изоляции с меньшим коэффициентом теплопроводности (_из) (например, перейти от верликулитовых с к минеральной вате с .

5 Перенос теплоты

через шаровую стенку

5.1 Перенос теплоты теплопроводностью

через шаровую стенку при ГУ I-рода

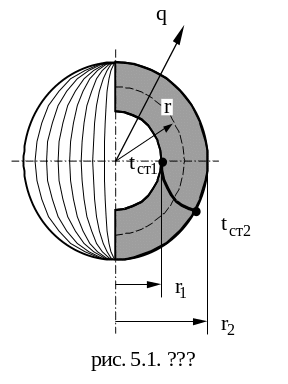
Имеем полый шар с внутренним ( ) и внешним ( ) радиусами и постоянным коэффициентом теплопроводности . Температура на внутренней поверхности – , а на внешней – , причём . Дифференциальное уравнение теплопроводности при стационарном режиме записывается в сферических координатах в виде (см. 2.11). Считаем, что температура меняется только вдоль радиуса r и не зависит от широты и долготы, поэтому дифференциальное уравнение теплопроводности преобразовывается в вид:

. (5.1)

Для решения данного дифференциального уравнения второго порядка запишем граничные условия:

при ,

при .

Если температура меняется вдоль радиуса шара, то закон Фурье имеет вид:

, Вт.

Поверхность шара равна

.

После двойного интегрирования уравнения (5.1) и определения постоянных интегрирования получаем выражение для теплового потока через шаровую стенку

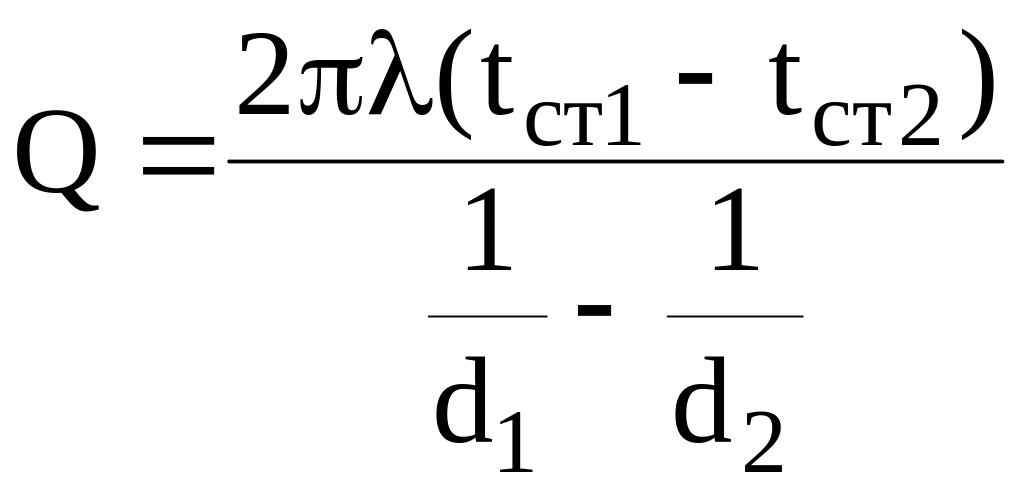. (5.2)

Плотность теплового потока через внутреннюю поверхность шара

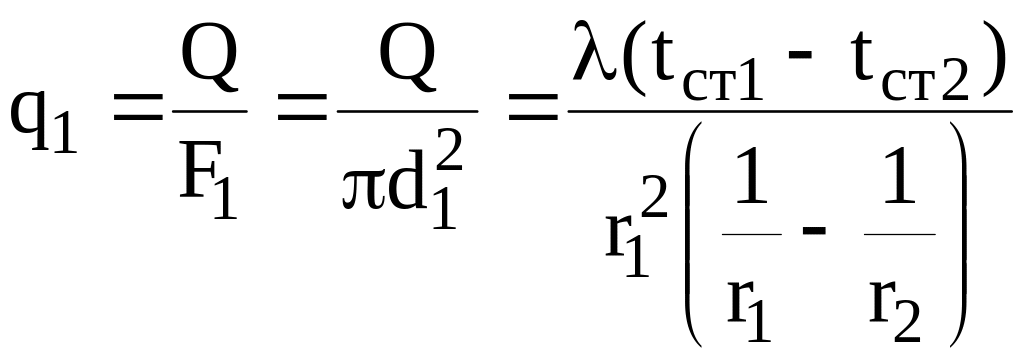, . (5.3)

Плотность теплового потока через наружную поверхность шара

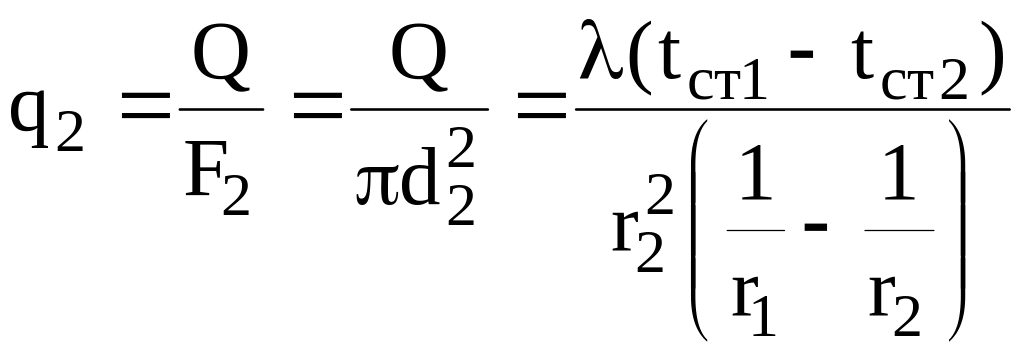, . (5.4)

Решением дифференциального уравнения (5.1) для температурного поля в шаровой стенке является

. (5.5)

Подставляя в уравнение (5.5) радиус r в метрах, можно определить температуру t в любой точке шаровой поверхности. Изотермические поверхности в этом случае являются шаровыми, т.е. температура в шаровой стенке меняется по закону гиперболы.

Для многослойной шаровой стенки из n-слоёв тепловой поток определяется из выражения:

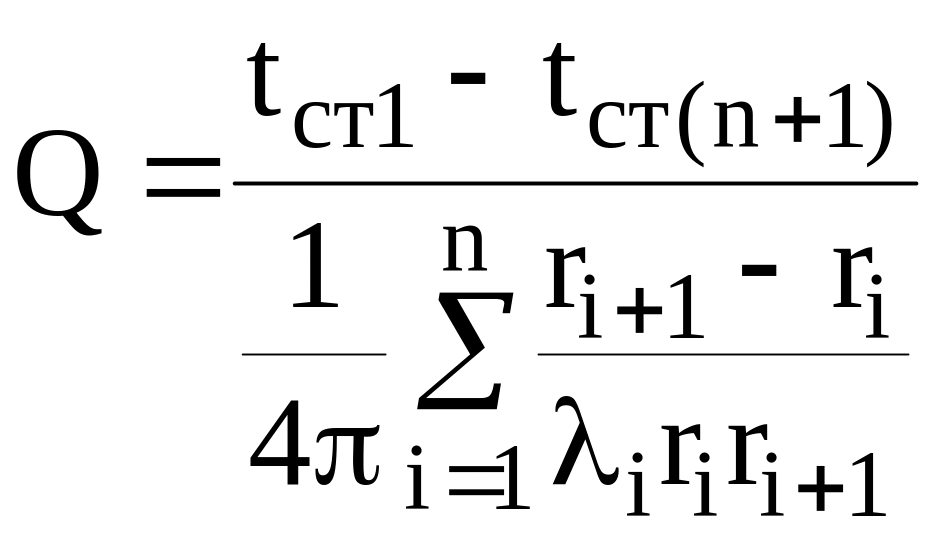. (5.6)

Значения и в (5.6) задаются.