1.4 Теплообмен при плёночной конденсации неподвижного чистого пара на вертикальной поверхности и при ламинарном режиме течения плёнки конденсата

Аналитическое решение задачи теплопроводности или теплоотдачи при ламинарном режиме течения плёнки конденсата впервые выполнил Нуссельт в 1916 г. Он сделал следующие допущения. Будем рассматривать стационарную задачу, и размер стенки (рис.1.5) в направлении оси OZ бесконечно велик. Кроме того:

1) силы инерции, возникающие в пленке конденсата, пренебрежимо малы по сравнению с силами вязкости и силами тяжести;

2) конвективным переносом теплоты в плёнке и теплопроводностью вдоль плёнки пренебрегаем, учитываем только теплопроводность поперёк плёнки;

3) трением на границе раздела паровой и жидкой фазы пренебрегаем;

4) температура внешней поверхности плёнки конденсата постоянна и равна t_s;

5) физические параметры конденсата не зависят от температуры;

6) плотность пара мала по сравнению с плотностью конденсата.

С учётом этих допущений дифференциальное уравнение энергии или теплопроводности имеет вид: ,

а уравнение Навье-Стокса: . (1.8)

Граничные усл-я: при : , ;при : , .

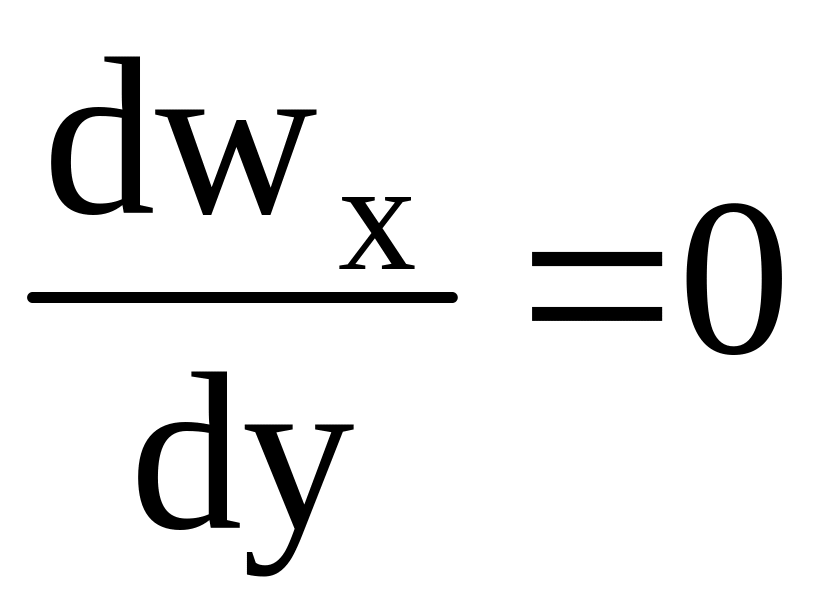Трение на границе раздела фаз отсутствует.

Систему (1.8) решил Нуссельт относительно толщины плёнки конденсата на расстоянии х от верха пластины. Он получил, что толщина плёнки определяется как: . (1.9)

Определяющей температурой является температура насыщения t_s, характерным размером – высота вертикальной стенки или высота трубы.

Т.к. 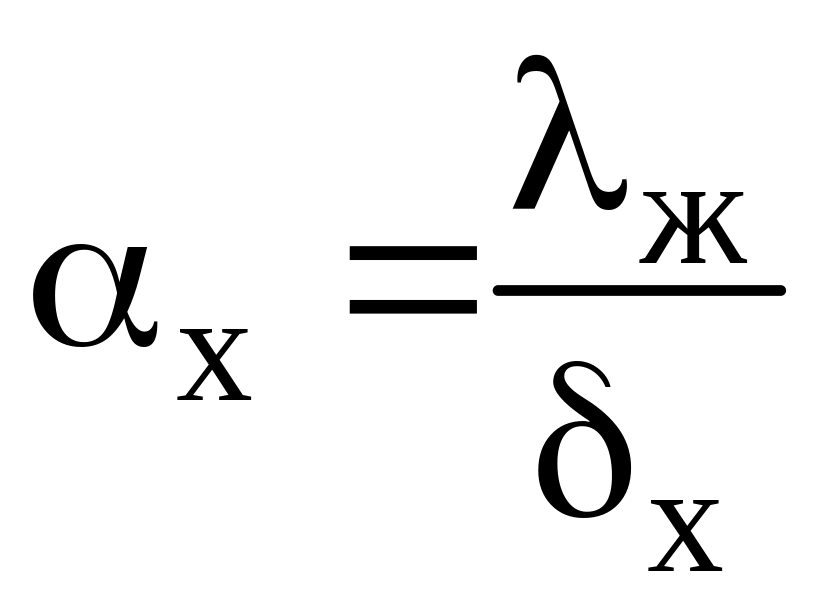, подставляя в это выражение _х, Нуссельт получил значение локального коэффициента теплоотдачи по высоте стенки:

. (1.10)

Среднее значение коэффициента теплоотдачи определяется как .

С учётом этого выражения . (1.11)

С увеличением t  уменьшается, q возрастает. Решение Нуссельта (1.11) хорошо совпадает с более точными решениями Лабунцова, хотя реальные коэффициенты теплоотдачи на 20% больше, чем рассчитанные по формуле (1.11). Академик Капица показал, что при , наступает волновой режим течения плёнки конденсата (рис. 1.7), это не учитывал Нуссельт, и именно за счёт волнового режима течения  больше на 20%, поэтому иногда для практических расчётов вместо коэффициента 0,943 подставляют 1,12. Для каждой жидкости своё значение Re_волн. Так, для воды , а ламинарный режим течения – при . С учётом влияния конвективного переноса теплоты в плёнке, зависимости физических свойств конденсата от температуры и волнового режима течения плёнки

,

где – поправка на конвективный перенос.

При числе подобия Кутателадзе и :

.

Поправка на изменение физических свойств

.

_v – поправка на волновой режим течения конденсата .

Формула (1.11) может быть преобразована к безразмерному виду.

Определяемым критерием является:

,

вводится безразмерная приведённая высота стенки, как некоторое число подобия Z , .

Ламинарный режим течения наступает при .

С учётом поправок , , мы получаем критериальную зависимость:

(1.12)

Следовательно: .

Решение Лабунцова в книге Краснощёкова.

При ламинарном режиме течения плёнки конденсата по вертикальной трубе: ,

,

,

, .

Обозначим через:

, ;

, .

Тогда:

.

Расход конденсата

, .

Кутателадзе обработал зависимости Нуссельта, Лабунцова, других авторов и свои эксперименты с помощью теории подобия и получил критериальные зависимости вида (при ламинарном режиме течения):

,

, (1.13)

, , , .

Число Кутателадзе представляет собой меру агрегатного состояния вещества к теплоте перегрева или переохлаждения одной из фаз относительно температуры фазового перехода.

Значение коэффициента теплопередачи, рассчитанного по формулам (1.8), (1.11) и (1.13) могут отличаться на 10-15%.

1.5 Смешанный и турбулентный режим

течения плёнки конденсата.

Т урбулентный режим течения плёнки конденсата поступает при и . Т.к. в верхней части стенки , то режим движения ламинарный. Средний коэффициент течения плёнки при ,

. (1.14)

Определяющая температура – температура насыщения; определяющий геометрический размер – высота стенки или высота трубы.

1.6 Конденсация на горизонтальных трубах

и на пучках труб

Нуссельт получил, что для наклонной стенки

,

где  – угол, образованный вертикалью и осью тела Х.

Произведя интегрирование по  выражение (1.8) от 0 до 180 он получил выражение для среднего коэффициента теплоотдачи по периметру горизонтальной трубы при плёночной конденсации пара и ламинарном режиме движения плёнки конденсата

(1.15)