
- •2 Билет.
- •3 Билет.
- •Алгоритм Описание
- •Вычитание векторов
- •Умножение вектора на число
- •Свойства линейных операций над векторами
- •Линейные комбинации векторов
- •§ 1. Ориентация пространства. Правые и левые тройки некомпланарных векторов.
- •§ 2. Скалярное произведение векторов.
- •§ 3. Векторное произведение векторов.
- •§4. Смешанное произведение векторов.
- •В координатной форме
- •[Править]Обозначения
- •[Править]Свойства коллинеарности
- •Линейно зависимые и линейно независимые системы векторов
- •1.Двумя точками (а и в).
- •2. Двумя плоскостями (; ).
- •3. Двумя проекциями.
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Угол между прямыми на плоскости
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •Расстояние от точки до прямой
- •Расстояние от точки до прямой
- •Угол между прямыми на плоскости
- •Уравнение плоскости
- •Угловой коэффициент в уравнении прямой. Геометрический смысл коэффициента.
- •Расстояние от точки до прямой
- •Взаимное расположение двух плоскостей (формулировки и примеры)
- •Угол между плоскостями
- •Прямая в пространстве
- •Числовые последовательности
- •Арифметические действия над числовыми последовательностями
- •Ограниченные и неограниченные последовательности
- •Бесконечно большие и бесконечно малые последовательности
- •Связь между бесконечно малыми и бесконечно большими последовательностями
- •Оновные свойства бесконечно малых последовательностей
- •Определения
- •[Править]Промежутки монотонности
- •[Править]Примеры
- •Способы определения
- •[Править]Свойства
- •Теорема о вложенных отрезках
- •Односторонний предел по Гейне
- •[Править]Односторонний предел по Коши
- •Теоремы о пределах
- •Второй замечательный предел
- •Исчисление бесконечно малых и больших
- •[Править]Бесконечно малая величина
- •[Править]Бесконечно большая величина
- •[Править]Свойства бесконечно малых
- •[Править]Сравнение бесконечно малых
- •[Править]Определения
- •[Править]Примеры сравнения
- •Определение непрерывности функции
- •Арифметические действия над непрерывными функциями
- •Определение
- •[Править]Существование
- •[Править]Примеры
- •[Править]Свойства
- •Понятие производной
- •Геометрический смысл производной
- •Производные и дифференциалы высших порядков
- •Дифференцируемость
- •[Править]Замечания
- •Дифференцирование функций, заданных параметрически
- •Следствие
- •Доказательство Лагранжа
- •Отношение бесконечно малых
- •[Править]Отношение бесконечно больших
- •Так почему же это является неопределённостью? Править
Следствие
Если непрерывная функция обращается в ноль в n различных точках, то ее производная обращается в ноль по крайней мере в n − 1 различных точках[1], причем эти нули производной лежат в выпуклой оболочке нулей исходной функции. Это следствие легко проверяется для случая действительных корней, однако имеет место и в комплексном случае.

Геометрический смысл теоремы.
Билет 45.
Доказательство Лагранжа
если производная от функции равна нулю, то функция является константой.
Это доказательство опирается на следующую лемму Вильсона: если p - простое число, то число (p-1)!+1 делится на p.
Чтобы не отвлекаться на доказательство этого вспомогательного факта, продемонстрирую лишь основную идею этого доказательства на примере простого числа 13. Для любого числа x, 2 ≤ x ≤ 11, найдется такое число y, 2 ≤ y ≤ 11, что x* y при делении на 13 дае в остатке 1. Действительно,
(13-1)!=12!=(2* 7)(3* 9)(4* 10)(5* 8)(6* 11)* 12,
и при этом все произведения в скобках при делении на 13 дают в остатке 1, а значит, 12! при делении на 13 даст в остатке 12, откуда (для выбранного нами числа 13) следует утверждение леммы Вильсона.
Из леммы Вильсона извлечем такое следствие: если p=4n+1, где n - натуральное число, то ((2n)!)2+1 делится на p. Действительно, из леммы Вильсона следует, что (4n)!+1делится на p, и теперь необходимое утверждение вытекает из слежующей выкладки:
(4n)!+1=(2n)!(2n+1)*...*(4n)+1= =(2n)!(p-2n)(p-2n-1)*...*(p-1)+1= =(2n)!(-1)2n(2n)!+pk+1 ≡ ((2n)!)2+1(mod p).
Обозначим (2n)! через N. Мы доказали, что N2≡ -1(mod p).
Теперь
нам предстоит преодолеть основную
трудность. Рассмотрим все пары целых
чисел (m,s),
такие что 0
≤ m ≤ [ ![]() ], 0≤
s≤ [
],
через [
] обозначена
целая часть числа
-
наибольшее целое число, не превосходящее
.
Число таких пар ([
]+1)2>p.
Значит, по крайней мере для
двух различных пар (m1,s1) и (m2,s2) остатки
от деления m1+Ns1 и m2+Ns2 на p одинаковы,
т. е. число a+Nb,
где a=m1-m2, b=s1-s2,
будет делиться на p.
При этом |a|≤[
], |b|
≤[
].
Но тогда число a2-N2 b2=(a+Nb)(a-Nb)делится
на p,
и значит, учитывая, что N2≡
-1(mod p),
получим, что a2+b2 делится
на p,
т. е. a2+b2=rp,
где r -
натуральное число (r≠,
ибо иначе пары были бы одинаковы). С
другой стороны, a2+b2≤
2[
]2<2p,
т. е. r=1,
и значит, a2+b2=p.
Теорема 2 доказана.
], 0≤
s≤ [
],
через [
] обозначена
целая часть числа
-
наибольшее целое число, не превосходящее
.
Число таких пар ([
]+1)2>p.
Значит, по крайней мере для
двух различных пар (m1,s1) и (m2,s2) остатки
от деления m1+Ns1 и m2+Ns2 на p одинаковы,
т. е. число a+Nb,
где a=m1-m2, b=s1-s2,
будет делиться на p.
При этом |a|≤[
], |b|
≤[
].
Но тогда число a2-N2 b2=(a+Nb)(a-Nb)делится
на p,
и значит, учитывая, что N2≡
-1(mod p),
получим, что a2+b2 делится
на p,
т. е. a2+b2=rp,
где r -
натуральное число (r≠,
ибо иначе пары были бы одинаковы). С
другой стороны, a2+b2≤
2[
]2<2p,
т. е. r=1,
и значит, a2+b2=p.
Теорема 2 доказана.
Теорема Больцано-Коши
Пусть на отрезке [α, β] функция f(x) определена, непрерывна и на концах отрезка принимает значения разных знаков, тогда на [α, β] содержится по крайней мере один корень уравнения f(x) = 0.
Доказать
теоремы Коши: если функция f(x) определена
в интервале ![]() и
ограничена в каждом конечном интервале
(a, b), то
а)
и
ограничена в каждом конечном интервале
(a, b), то
а) ![]() б)
б) ![]()
![]() ,
,
Билет 46.
Правило
Бернулли[1]-Лопита́ля —
метод нахождения пределов
функций, раскрывающий
неопределённости вида 0
/ 0 и ![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
Точная формулировка
Условия:
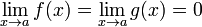 или
или 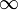 ;
; и
и  дифференцируемы
в проколотой окрестности
;
дифференцируемы
в проколотой окрестности
; в
проколотой окрестности
;
в
проколотой окрестности
;существует
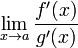 ,
,
тогда
существует ![]() .
.
Пределы также могут быть односторонними.
