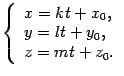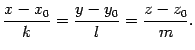Прямая в пространстве
Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.
Итак,
если уравнения двух непараллельных
плоскостей -- 
и 
,
то прямая, являющаяся их линией
пересечения, задается системой уравнений
|
(11.11) |
И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.
Уравнения (11.11) называют общими уравнениями прямой в пространстве.
Замечание 11.2 Любые попытки с помощью преобразований уравнений системы (11.11) получить одно (линейное) уравнение, задающее прямую, обречены на неудачу. Одно уравнение -- это уравнение плоскости.
Общие уравнения прямой "неудобны" для получения информации о положении прямой.
Например, чтобы найти координаты какой-нибудь точки на прямой, нужно провести довольно сложные вычисления. А именно, задать произвольно какую-нибудь координату, подставить ее в систему (11.11) и из получившейся системы двух уравнений с двумя неизвестными найти две остальные координаты. Причем может оказаться, что полученная система не имеет решений. Тогда нужно произвольно задать другую координату и из системы найти две оставшиеся координаты.
Пример 11.2 Требуется найти какую-нибудь точку на прямой
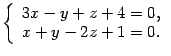
Решение. Положим 
.
Получим систему
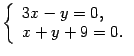
Решая
ее, находим 
, 
.
Ответ: 
.
Можно задать прямую в пространстве и другим способом.
Ненулевой вектор, лежащий на прямой (параллельный ей) называется направляющим вектором прямой.
Пусть
для прямой 
известны
ее направляющий вектор 
и
точка 
,
лежащая на этой прямой. Пусть 
--
произвольная (текущая) точка прямой
.
Обозначим через
и r радиус-векторы
точек
и
соответственно
(рис. 11.11).
Рис.11.11.Векторное уравнение прямой
Тогда
вектор
коллинеарен
вектору p и,
следовательно, 
,
где 
--
некоторое число. Из рис. 11.11 видно, что
|
(11.12) |
Это уравнение называется векторным уравнением прямой или уравнением в векторной форме. При каждом значении параметра мы будем получать новую точку на прямой .
Замечание 11.3
Если в качестве параметра
взять
время, то точка
будет
двигаться по прямой со скоростью 
,
причем в момент времент 
ее
положение совпадает с точкой
.
Вектор скорости точки совпадает с
вектором p.
От
векторного соотношения (11.12)
перейдем к соотношениям координат. Так
как 
--
координаты точки
,
то 
, 
, 
.
Из формулы (11.12)
получим
|
(11.13) |
Полученная система уравнений называется параметрическими уравнениями прямой.
Обратим внимание на то, что по параметрическим уравнениям легко установить направляющий вектор прямой и координаты одной из ее точек. Коэффициенты перед параметром дают координаты направляющего вектора, а свободные члены в правой части -- координаты точки на прямой.
Так как направляющий вектор прямой определяется с точностью до умножения на число, отличное от нуля, а в качестве точки можно взять любую точку прямой, то одна и та же прямая может задаваться бесконечным множеством систем параметрических уравнений. Причем разные системы могут быть не похожими друг на друга.
Из уравнений (11.13) выразим параметр :
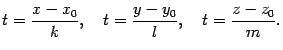
Так как во всех трех соотношениях параметр имеет одно и то же значение, то
|
(11.14) |
Эти уравнения называются каноническими1 уравнениями прямой.
Замечание 11.4
В канонических уравнениях прямой
допускается в знаменателе писать 0. Это
не означает, что можно выполнить деление
на 0. Просто из канонических уравнений
мы получаем информацию о том, что
направляющий вектор прямой имеет
координаты 
,
из которых одна нулевая.
Пример 11.3 Прямая с каноническими уравнениями
имеет
направляющий вектор 
.
Замечание 11.5 Канонические уравнения прямой (11.14) нельзя рассматривать как одно уравнение (в них два знака "=" и следовательно, два уравнения). Они составляют своеобразным способом записанную систему из двух уравнений
Билет 20.
Взаимное расположение двух прямых в пространстве |
|
|
Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями.
Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость и точке, которая не лежит на первой прямой, то эти прямые скрещиваются. На рис. 26 прямая a лежит в плоскости , а прямая с пересекает в точке N. Прямые a и с — скрещивающиеся. Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой.
На рис. 26 прямые a и b скрещиваются. Черен прямую а проведена плоскость || b (в плоскости указана прямая a1 || b). Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты. |
Билет 21.
Прямая и плоскость в пространстве могут:
а) не иметь общих точек;
б) иметь ровно одну общую точку;
в) иметь хотя бы две общие точки.
На рис. 30 изображены все эти возможности.
В случае а) прямая b параллельна плоскости : b || .
В
случае б) прямая l пересекает плоскость
в
одной точке О; l 
=
О.
В
случае в) прямая а принадлежит
плоскости
:
а
или а 
.
Теорема. Если прямая b параллельна хотя бы одной прямой а, принадлежащей плоскости , то прямая параллельна плоскости .
Предположим, что прямая m пересекает плоскость в точке Q.Если m перпендикулярна каждой прямой плоскости , проходящей через точку Q, то прямая m называется перпендикулярной к плоскости .
Трамвайные рельсы иллюстрируют принадлежность прямых плоскости земли. Линии электропередачи параллельны плоскости земли, а стволы деревьев могут служить примерами прямых, пересекающих поверхность земли, некоторые перпендикулярные плоскости земли, другие — не перпендикулярные (наклонные).
Взаимное расположение двух плоскостей.
Плоскости могут совпадать, быть параллельными или пересекаться по прямой.
рис.3.
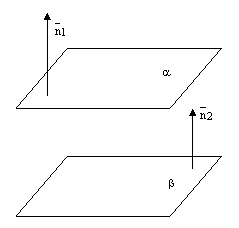
рис.4.
рис.5.
Теорема. Пусть
и 
– общие уравнения двух плоскостей. Тогда:
1)
если 
,
то плоскости совпадают;
2)
если 
,
то плоскости параллельны;
3)
если 
или 
,
то плоскости пересекаются и системауравнений
(6)
является уравнениями прямой пересечения данных плоскостей.
Доказательство. Первое и второе условия теоремы равносильны коллинеарности нормальных векторов данных плоскостей:
.
Если 
,
то 
, 
, 
, 
и уравнение плоскости 
принимает
вид:
Коэффициент
пропорциональности k не может быть равен
нулю, т.к. 
и
при 
получаем,
что 
,
что противоречит определению нормального
вектора. Следовательно,уравнение плоскости
совпадает
с уравнением плоскости 
,
а это означает, что плоскости совпадают.
Если , то это означает коллинеарность нормальныхвекторов обеих плоскостей, а значит плоскости либо параллельны, либо совпадают. Но в этом случае плоскости не могут совпадать и остается единственная возможность их параллельности.
Третье условие теоремы равносильно тому, что нормальные векторыплоскостей не коллинеарные, а потому они не совпадают и не параллельны, а следовательно, они пересекаются. Из геометрии известно, что линия пересечения двух плоскостей является прямой.
Точка М лежит на прямой пересечения двух плоскостей и тогда и только тогда, когда она лежит одновременно на обеих плоскостях и еекоординаты удовлетворяют обоим уравнениям системы (6), т.е. являются решением этой системы. А это означает, что система (6) является уравнениями прямой пересечения плоскостей, ч.т.д.
Теорема доказана.
п.4. Взаимное расположение прямой и плоскости в пространстве.
Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.
рис.6.
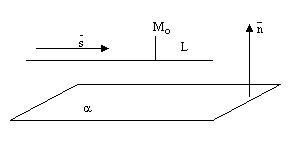
рис.7.
рис.8.
Теорема. Пусть плоскость задана общим уравнением
,
а прямая L задана каноническими уравнениями
или параметрическими уравнениями
, 
,
в
которых 
– координаты нормального вектора плоскости
, 
– координаты произвольной
фиксированной точки прямой L, 
–
координаты направляющего вектора прямой L. Тогда:
1)
если 
,
то прямая L пересекает плоскость
в
точке,координаты которой 
можно
найти из системы уравнений
;
(7)
2)
если 
и 
,
то прямая лежит на плоскости;
3)
если
и 
,
то прямая параллельна плоскости.
Доказательство.
Условие 
говорит
о том, что вектроры 
и 
не
ортогональны, а значит прямая не
параллельна плоскости и не лежит в
плоскости, а значит пересекает ее в
некоторой точке М. Координаты точки
М удовлетворяют как уравнению плоскости,
так и уравнениям прямой, т.е. системе
(7). Решаем первое уравнение системы (7)
относительно неизвестной t и затем,
подставляя найденное значение t в
остальныеуравнения системы,
находим координаты искомой
точки.
Если 
,
то это означает, что 
.
А такое возможно лишь тогда, когда прямая
лежит на плоскости или параллельна ей.
Если прямая лежит на плоскости, то любая
точка прямой является точкой плоскости
икоординаты любой
точки прямой удовлетворяют уравнению
плоскости. Поэтому достаточно проверить,
лежит ли на плоскости точка
.
Если
,
то точка 
–
лежит на плоскости, а это означает, что
и сама прямая лежит на плоскости.
Если , а , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.
Теорема доказана.
Билет 22.
Теорема
Две
скрещивающиеся прямые имеют общий
перпендикуляр, и при том только один.
Он является общим перпендикуляром
параллельных плоскостей, проходящих
через эти прямые.
Доказательство
Пусть
a и b – данные скрещивающиеся прямые.
Проведем через них параллельные плоскости
α и β. Прямые, пересекающие прямую a и
перпендикулярные плоскости α, лежат в
одной плоскости (γ). Эта плоскость
пересекает плоскость β по прямой a`,
параллельной a. Пусть B – точка пересечения
прямых a` и b. Тогда прямая AB, перпендикулярная
плоскости α, перпендикулярна и плоскости
β, так как β параллельна α. Отрезок AB –
общий перпендикуляр плоскостей α и β,
а значит, и прямых a и b.
Докажем,
что этот общий перпендикуляр единственный.
Допустим, что у прямых a и b есть другой
общий перпендикуляр CD. Проведем через
точку С прямую b`, параллельную b. Прямая
CD перпендикулярна прямой b, а значит, и
b`. Так как она перпендикулярна прямой
a, то она перпендикулярна плоскости α,
а значит, параллельна прямой AB. Выходит,
что через прямые AB и CD, как через
параллельные, можно провести плоскость.
В этой плоскости будут лежать наши
скрещивающиеся прямые AC и BD, а это
невозможно, что и требовалось доказать.
Билет 23 .