Бесконечно большие и бесконечно малые последовательности

   Определение. Последовательность { х_n} называется бесконечно большой, если для как угодно большого любого положительного числа Асуществует номер N, зависящий от этого числа А, такой, что для всех последующих номеров n > N выполняется неравенство | x_n | > A:

   Замечание. Очевидно, что любая бесконечно большая последовательность является неограниченной. Однако неограниченная последовательность может и не быть бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3, …, 1, n + 1, … не является бесконечно большой, поскольку при A > 1 неравенство | x_n| > A выполняется не для всех элементов x_n с нечетными номерами.    Определение. Последовательность {α_n} называется бесконечно малой, если для любого как угодно малого положительного числа ε > 0 существует номер N, зависящий от этого ε, такой, что для любых n > N выполняется неравенство |α_n| < ε:

Связь между бесконечно малыми и бесконечно большими последовательностями

   Теорема 1. Если { х_n} — бесконечно большая последовательность и все ее члены отличны от нуля, то последовательность

бесконечно малая, и, обратно, если {α_n} — бесконечно малая последовательность и все её члены отличны от нуля {α_n} ≠ 0, то последовательность { 1 / α_n } – бесконечно большая.   Доказательство. Пусть { х_n} — бесконечно большая последовательность. Возьмем любое как угодно малое положительное число ε > 0 и положим

Согласно определению для этого существует такой номер N , что при n > N будет | x_n | > A. Отсюда получаем, что

для всех n > N. А это значит, что последовательность

бесконечно малая.

Оновные свойства бесконечно малых последовательностей

   Теорема.Сумма (разность) двух бесконечно малых последовательностей есть бесконечно малая последовательность.   Доказательство. Пусть {α_n} и {β_n} — бесконечно малые последовательности. Требуется доказать, что последовательность α_n ± β_n тоже бесконечно малая. Пусть ε – произвольное как угодно малое положительное число, N₁ – номер, начиная с которого выполняется неравенство

,

N₂ - номер, начиная с которого выполняется неравенство

.

(Такие номера N₁ и N₂ найдутся по определению бесконечно малой последовательности.) Возьмем

N = max {N₁, N₂},

тогда при n > N будут одновременно выполняться два неравенства:

и

Следовательно, при n > N имеем

Это значит, что последовательность

α_n ± β_n

бесконечно малая.   Следствие. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.   Теорема 3. Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.   Доказательство. Пусть {α_n} и {β_n} — бесконечно малые последовательности. Требуется доказать, что последовательность {α_n·β_n} тоже является бесконечно малой. Так как последовательность {α_n} бесконечно малая, то для любого как угодно малого положительного числа ε> 0 существует номер N₁, зависящий от ε, такой, что для всех последующих номеров n > N₁ ,будет выполнено неравенство

а так как {β_n) – также бесконечно малая последовательность, то для любого как угодно малого положительного числа ε> 0 существует номер N₂, зависящий от ε, такой, что для всех последующих номеров n > N₂ ,будет выполнено неравенство

Возьмём N = max{N₁, N₂}, тогда при n > N будут одновременно выполняться оба неравенства. Следовательно,

Это означает, что последовательность {α_n·β_n} бесконечно малая.   Следствие. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.    Теорема 4.Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.   Доказательство. Пусть {x_n} – ограниченная, а {α_n} – бесконечно малая последовательности. Требуется доказать, что последовательность{x_n·α_n} бесконечно малая. Так как последовательность {x_n} ограничена, то существует число А > 0 такое, что любой элемент числовой последовательности {x_n} удовлетворяет неравенству | x_n| ≤ A. Возьмем любое как угодно малое положительное число ε > 0. Поскольку последовательность {α_n} бесконечно малая, то для любого как угодно малого положительного числа ε/ A существует номер N такой, что при всех n > Nвыполняется неравенство

 

Следовательно, при n > N имеем

Это означает, что последовательность {x_n·α_n} является бесконечно малой числовой последовательностью.   Следствие. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.

Билет 25.

Понятие последовательности

Последовательностью элементов множества E называется отображение

т. е. функция, которая каждому натуральному числу   ставит в соответствие элемент  .

Для записи последовательности употребляем обозначения (x_n), или x₁, x₂, ..., x_n, ..., или x_n = f(n),  .

Элементы x₁, x₂, ..., x_n, ... называются членами последовательности, а x_n - общим членом последовательности.

Множество E может быть различным, например: R, R^m, C[a, b],   и т.д. Если E = R, то последовательность называется числовой, если E = R^m, - векторной, если E = C[a, b], - функциональной, если E =   - матричной и т. д. В каждом из этих случаев множество всевозможных последовательностей образует векторное нормированное, а следовательно, и метрическое пространство.

Сходящиеся последовательности и их свойства

Рассмотрим числовые последовательности.

Последовательность (x_n) действительных чисел называется сходящейся, если существует действительное число a и для произвольного ε > 0 существует натуральное число m такое, что для всех n > m справедливо неравенство |x_n - a| < ε.

При этом число a называют пределом последовательности (x_n), что символически записывают

 или x_n → a при n → ∞.

С помощью логических символов определение запишется следующим образом: числовая последовательность (x_n) называетсясходящейся, если

Сходящиеся последовательности в метрическом пространстве

Последовательность (x_n) элементов метрического пространства E называется сходящей, если существуют элемент   и для любого ε > 0 натуральное число m такое, что   справедливо неравенство ρ(x_na) < ε.

В этом определении натуральное число m можно заменить положительным действительным числом α, поскольку из неравенства n> α следует n > [α] = m.

Если в R^m задана последовательность с членами

такая, что существует  , то эта последовательность сходится и справедливо равенство

Аналогично, если в   задана последовательность

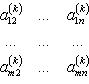
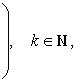
такая, что  , то эта последовательность сходится и справедливо равенство

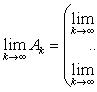
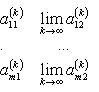
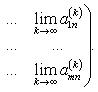
Билет 26 .

Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей.