
- •2 Билет.
- •3 Билет.
- •Алгоритм Описание
- •Вычитание векторов
- •Умножение вектора на число
- •Свойства линейных операций над векторами
- •Линейные комбинации векторов
- •§ 1. Ориентация пространства. Правые и левые тройки некомпланарных векторов.
- •§ 2. Скалярное произведение векторов.
- •§ 3. Векторное произведение векторов.
- •§4. Смешанное произведение векторов.
- •В координатной форме
- •[Править]Обозначения
- •[Править]Свойства коллинеарности
- •Линейно зависимые и линейно независимые системы векторов
- •1.Двумя точками (а и в).
- •2. Двумя плоскостями (; ).
- •3. Двумя проекциями.
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Угол между прямыми на плоскости
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •Расстояние от точки до прямой
- •Расстояние от точки до прямой
- •Угол между прямыми на плоскости
- •Уравнение плоскости
- •Угловой коэффициент в уравнении прямой. Геометрический смысл коэффициента.
- •Расстояние от точки до прямой
- •Взаимное расположение двух плоскостей (формулировки и примеры)
- •Угол между плоскостями
- •Прямая в пространстве
- •Числовые последовательности
- •Арифметические действия над числовыми последовательностями
- •Ограниченные и неограниченные последовательности
- •Бесконечно большие и бесконечно малые последовательности
- •Связь между бесконечно малыми и бесконечно большими последовательностями
- •Оновные свойства бесконечно малых последовательностей
- •Определения
- •[Править]Промежутки монотонности
- •[Править]Примеры
- •Способы определения
- •[Править]Свойства
- •Теорема о вложенных отрезках
- •Односторонний предел по Гейне
- •[Править]Односторонний предел по Коши
- •Теоремы о пределах
- •Второй замечательный предел
- •Исчисление бесконечно малых и больших
- •[Править]Бесконечно малая величина
- •[Править]Бесконечно большая величина
- •[Править]Свойства бесконечно малых
- •[Править]Сравнение бесконечно малых
- •[Править]Определения
- •[Править]Примеры сравнения
- •Определение непрерывности функции
- •Арифметические действия над непрерывными функциями
- •Определение
- •[Править]Существование
- •[Править]Примеры
- •[Править]Свойства
- •Понятие производной
- •Геометрический смысл производной
- •Производные и дифференциалы высших порядков
- •Дифференцируемость
- •[Править]Замечания
- •Дифференцирование функций, заданных параметрически
- •Следствие
- •Доказательство Лагранжа
- •Отношение бесконечно малых
- •[Править]Отношение бесконечно больших
- •Так почему же это является неопределённостью? Править
[Править]Примеры сравнения
При
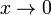 величина x5 имеет
высший порядок малости относительно x3,
так как
величина x5 имеет
высший порядок малости относительно x3,
так как 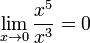 .
С другой стороны, x3 имеет
низший порядок малости относительно x5,
так как
.
С другой стороны, x3 имеет
низший порядок малости относительно x5,
так как 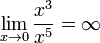 .
.
С использованием О-символики полученные результаты могут быть записаны в следующем виде x5 = o(x3).
 то
есть при
функции f(x)
= 2x2 +
6x и g(x)
= x являются
бесконечно малыми величинами одного
порядка.
то
есть при
функции f(x)
= 2x2 +
6x и g(x)
= x являются
бесконечно малыми величинами одного
порядка.
В данном случае справедливы записи 2x2 + 6x = O(x) и x = O(2x2 + 6x).
При бесконечно малая величина 2x3 имеет третий порядок малости относительно x, поскольку
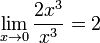 ,
бесконечно малая 0,7x2 —
второй порядок, бесконечно малая
,
бесконечно малая 0,7x2 —
второй порядок, бесконечно малая  —
порядок 0,5.
—
порядок 0,5.
Билет 34.
Определение непрерывности функции
Пусть функция f (x) определена в некоторой окрестности точки х0. Функция f (x) называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т. е.
![]() (5.1)
(5.1)
или
(
ε
> 0 ) ( ![]() δ
= δ (ε, x0)
> 0 ) (
| x
- x0 |
< δ ) : | f ( x )
− f ( x0)
| < ε
δ
= δ (ε, x0)
> 0 ) (
| x
- x0 |
< δ ) : | f ( x )
− f ( x0)
| < ε
Заметим,
что в этом случае окрестность точки х0 не
является выколотой, в отличие от
определения предела.
Напомним,
что δ – окрестностью точки х0 называют
множество всех точек х,
удалённых от точки х0 на
расстояние, меньшее чем δ. Для непрерывности
функции в точке требуется выполнение
двух условий: существование предела
функции в данной точке и совпадение
этого предела с тем значением, которое
функция принимает в этой точке. Так
как ![]() ,
то соотношение (5.1) можно записать в
следующем виде:
,
то соотношение (5.1) можно записать в
следующем виде:

т. е. для непрерывной функции можно переставить знак функции и знак предела. Если функция непрерывна в точке х0, то она определенна в этой точке, т.е. существует f (x0). Заметим, что при определении предела функции в точке х0 этого не требовалось. Приведем еще одно определение непрерывности функции, которое по существу является перефразировкой данного определения непрерывности функции в данной точке. Если
![]()
то функция непрерывна в этой точке. Это определение вытекает из свойства предельного перехода функции в данной точке. Приведем еще одно определение непрерывности функции, которое является перефразированной первого определения непрерывности. Перенесем в равенстве (5.1) f (x0) под знак предела. Так как условие х → х0 и (х − х0) → 0 равносильны, то получаем
![]() (5.2)
(5.2)
Разность Δx = x - x0 называется приращением аргумента х в точке x0, разность Δy = f (x) − f (x0) называется приращением функции в точке х0, вызванным приращением аргумента Δх (рис. 5.13). При фиксированной точке х0 величина Δу является функцией аргумента Δ х. Равенство (5.2) в новых обозначениях принимает вид
![]() (5.3)
(5.3)
(5.3) является свойством непрерывной функции, которое можно сформулировать так: функция f (x) является непрерывной в точке х0, если ее приращение в этой точке является бесконечно малой функцией при Δх → 0.
Арифметические действия над непрерывными функциями
Пусть функции f (x) и g (x) непрерывны в точке х0. Тогда функции f (x) ± g (x), f (x)·g (x) и f (x) : g (x) также непрерывны в этой точке (в последнем случае предполагается g (х0) ≠ 0).
Билет 35.
Классификация точек разрыва функции Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
При этом возможно следующие два случая:
Такая точка называется точкой устранимого разрыва.
Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. |
||||||
Пример 1 |
||||||
|
||||||
Исследовать
функцию Решение. Данная функция не определена в точках x = −1 и x = 1. Следовательно, функция имеет разрывы в точкахx = ±1. Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках. Поскольку левосторонний предел при x = −1 равен бесконечности, то данная точка является точкой разрыва второго рода. Аналогично, левосторонний предел в точке x = 1 равен бесконечности. Эта точка также является точкой разрыва второго рода. |
||||||
Пример 2 |
||||||
|
||||||
Показать,
что функция Решение. Очевидно,
данная функция не определена при x
= 0.
Поскольку sin x является
непрерывной функцией для всехx,
то искомая функция
также
непрерывна при всех x за
исключением точки x
= 0.
Так
как которая будет непрерывной при любом действительном x. |
||||||
Пример 3 |
||||||
|
||||||
Найти
точки разрыва функции Решение. Данная функция существует при всех значениях x, однако она состоит из двух различных функций и, поэтому, не является элементарной. Исследуем "поведение" этой функции вблизи точки x = 0, где ее аналитическое выражение изменяется. Вычислим односторонние пределеы при x = 0. Следовательно, функция имеет точку разрыва первого рода при x = 0. Скачок функции в этой точке равен При всех других значениях x функция является непрерывной, поскольку обе составляющие функции слева и справа от точки x = 0 представляют собой элементарные функции без точек разрыва. |
||||||
Пример 4 |
||||||
|
||||||
Найти
точки разрыва функции Решение. Данная элементарная функция определена для всех x, исключая точку x = 0, где она имеет разрыв. Найдем односторонние пределы в этой точке. Видно, что в точке x = 0 существует разрыв первого рода (рисунок 2).
|
||||||
Пример 5 |
||||||
|
||||||
Найти
точки разрыва функции Решение.
Функция
определена и непрерывна при всех x,
за исключением точки
Так как значения односторонних пределов конечны, то, следовательно, в точке существует разрыв первого рода. График функции схематически показан на рисунке 3. |
Билет 36.
Основные свойства непрерывных функций
Функция f: [a, b] → R называется непрерывной на сегменте [a, b], если она непрерывна на интервале ]a, b[ и в точке aнепрерывна справа, а в точке b - слева.
Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], тогда:
1) она ограничена на этом сегменте;
2)
если ![]()
![]()
![]() ,
то на сегменте [a, b]
существуют точки x1 и x2 такие,
что f(x1)
= m, f(x2)
= M (теорема
Вейерштрасса);
,
то на сегменте [a, b]
существуют точки x1 и x2 такие,
что f(x1)
= m, f(x2)
= M (теорема
Вейерштрасса);
3)
она принимает на каждом сегменте ![]()
![]() ,
все промежуточные значения между f(α)
и f(β)
(теорема
Коши).
,
все промежуточные значения между f(α)
и f(β)
(теорема
Коши).
В частности, если f(α)f(β) < 0, то найдется такое значение γ (α < γ < β), то f(γ) = 0.
Функция f: ]a, b[ → R называется кусочно-непрерывной на интервале ]a, b[, если она непрерывна во всех точках этого интервала, кроме конечного числа точек разрыва первого рода и конечного числа точек устранимого разрыва.
Билет 37.
Сложная функция
Сложная
функция,
функция от функции. Если величина y
является функцией от u, то
есть у
= f (u), а и, в
свою очередь, функцией от х, то
есть u
= j(х), то у является
С. ф. от х, то
есть y =
f [(x)], определённой
для тех значенийх, для
которых значения j(х)
входят в множество определения
функции f (u). В
таком случае говорят, что уявляется
С. ф. независимого аргумента х, а u
— промежуточным
аргументом. Например, если у
= u2,
u = sinx, тоу =
sin2х для
всех значений х. Если
же, например, у = ![]() ,
u = sinx,
то у
=
,
u = sinx,
то у
= ![]() , причём,
если ограничиваться действительными
значениями функции, С. ф. у как
функция х определена
только для таких значений х, для
которых sin ³ 0, то есть для
, причём,
если ограничиваться действительными
значениями функции, С. ф. у как
функция х определена
только для таких значений х, для
которых sin ³ 0, то есть для ![]() , где k
= 0,
± 1, ± 2,...
, где k
= 0,
± 1, ± 2,...
Производная С. ф. равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по независимому аргументу. Это правило (цепное правило) распространяется на С. ф. с двумя, тремя и т. д. промежуточными аргументами: если у = f (u1), u1 = j(u2),..., uk-1= jk-1(uk), uk = jk (x), то
![]()
Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.



 ,
то в данной точке существует устранимый
разрыв. Мы можем сконструировать новую
функцию
,
то в данной точке существует устранимый
разрыв. Мы можем сконструировать новую
функцию
 ,
если они существуют.
,
если они существуют.
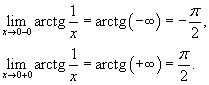


 ,
если таковые существуют.
,
если таковые существуют.