Дифференцирование функций, заданных параметрически

Пусть даны два уравнения

x=x(t),y=y(t), где t Î [T1, T2].

(1)

Каждому значению t из [T₁, T₂] соответствуют определенные значения x и y. Если рассматривать значения x и y как координаты точки на плоскости xOy, то каждому значению t будет соответствовать определенная точка плоскости. Когда tизменяется от T₁ до T₂, эта точка на плоскости описывает некоторую кривую. Уравнения (1) называютсяпараметрическими уравнениями этой кривой, t называется параметром, а способ задания кривой уравнениями (1) называется параметрическим.

Предположим, что функция x=x(t) имеет обратную t=t(x). Тогда, очевидно, у является функцией от x: y=y[t(x)]. Следовательно, уравнения (1) определяют y как функцию от x, и говорят, что функция y от x задается параметрически.

При рассмотрении функций, заданных параметрически, исключение параметра не всегда возможно. Во многих случаях удобнее задавать различные значения t и затем вычислять соответствующие значения аргумента x и функции y.

Пример. Пусть кривая задана параметрическими уравнениями:

Построим эту кривую на плоскости, придавая различные значения параметру t и находя соответствующие значения х и у.

При t =0 M(R, 0). 

Таким образом, получаем окружность с центром в начале координат, радиуса R. Здесь t обозначает угол, образованный радиусом, проведенным в некоторую точку окружности М(x, y), и осью Ox.

Если исключим из этих уравнений параметр t, то получим уравнение окружности, содержащее только x и y. Возводя в квадрат параметрические уравнения и складывая их, находим:

x²+ y²=R²(cos²t + sin²t) или x²+ y²=R².

Выведем правило нахождения производных функций, заданных параметрически. Пусть x=x(t), y=y(t), причем на некотором отрезке [T₁, T₂] функции x(t) и y(t) дифференцируемы и x' ≠ 0.

Т.к. у – функция, зависящая от переменной x, то будем считать, что функция x=x(t) имеет обратную t=t(x).

Будем обозначать: y_x' – производная функции по переменной x, y_t', x_t', t_x' – соответственно производные по t и х.

Воспользовавшись правилом дифференцирования сложной функции, получим  . Производную t_x' найдем по правилу дифференцирования обратной функции  .

Окончательно,  .

Итак,

Полученную функцию   можно рассматривать как функцию, заданную параметрически:  .

Используя эту формулу, можно находить и производные высших порядков функций, заданных параметрически. Найдем  . По определению второй производной  . Учитывая, что y_x' есть функция параметра t, y_x'=f(t),получаем:

Примеры.

1. , y = arcsin (t–1). Найдем  .

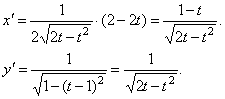
Следовательно,  .

2. Найти угловой коэффициент касательной к циклоиде x = a·(t – sin t), y = a·(1 – cost)

в произвольной точке (0 ≤t≤ 2·π).

Угловой коэффициент касательной  .

x' = a·(1 – cost) ,y' = a·sin t. Поэтому  .

3. 

Найти  .

Билет 44.

Теорема Ферма

Для любого натурального числа n > 2уравнение

не имеет натуральных решений a, b и c.

Теорема Ролля

Если вещественная функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.