Второй замечательный предел

 или 

Доказательство второго замечательного предела:

Доказательство для натуральных значений x  [показать]

   Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что  . Рассмотрим два случая:

1. Пусть  . Каждое значение x заключено между двумя положительными целыми числами:  , где   — это целая часть x.

Отсюда следует:  , поэтому

.

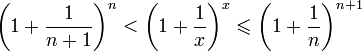Если  , то  . Поэтому, согласно пределу  , имеем:

.

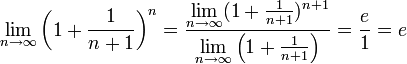
П о признаку (о пределе промежуточной функции) существования пределов  .

2. Пусть  . Сделаем подстановку − x = t, тогда

.

Из двух этих случаев вытекает, что   для вещественного x.    

Следствия

1. 

2. 

3. 

4. 

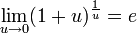
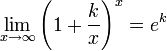
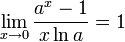5.  для  , 

6. 

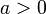примеры

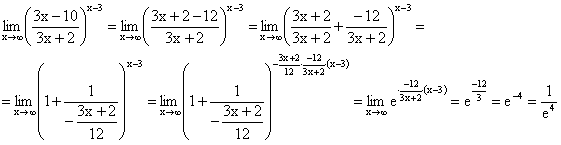
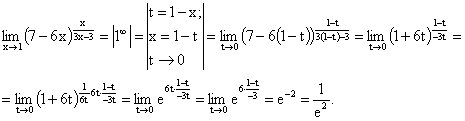
Билет 33 .

Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Исчисление бесконечно малых и больших

Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная суммабесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.

[Править]Бесконечно малая величина

Последовательность a_n называется бесконечно малой, если  . Например, последовательность чисел   — бесконечно малая.

Функция называется бесконечно малой в окрестности точки x₀, если  .

Функция называется бесконечно малой на бесконечности, если   либо  .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то f(x) − a = α(x),  .

[Править]Бесконечно большая величина

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функцияxsin x, неограниченная с обеих сторон, не является бесконечно большой при  .

Последовательность a_n называется бесконечно большой, если  .

Функция называется бесконечно большой в окрестности точки x₀, если  .

Функция называется бесконечно большой на бесконечности, если   либо  .

[Править]Свойства бесконечно малых

• Сумма конечного числа бесконечно малых — бесконечно малая.

• Произведение бесконечно малых — бесконечно малая.

• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

• Если a_n — бесконечно малая последовательность, сохраняющая знак, то   — бесконечно большая последовательность.

[Править]Сравнение бесконечно малых

Отношение бесконечно малых величин образует так называемую неопределённость  .

[Править]Определения

Допустим, у нас есть бесконечно малые при одном и том же   величины α(x) и β(x) (либо, что не важно для определения, бесконечно малые последовательности).

• Если 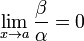 , то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).

• Если 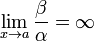 , то β — бесконечно малая низшего порядка малости, чем α. Соответственно α = o(β).

• Если 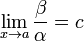  (предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.

Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).

• Если   (предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.

Для вычисления подобных пределов удобно использовать правило Лопиталя.