
- •2 Билет.
- •3 Билет.
- •Алгоритм Описание
- •Вычитание векторов
- •Умножение вектора на число
- •Свойства линейных операций над векторами
- •Линейные комбинации векторов
- •§ 1. Ориентация пространства. Правые и левые тройки некомпланарных векторов.
- •§ 2. Скалярное произведение векторов.
- •§ 3. Векторное произведение векторов.
- •§4. Смешанное произведение векторов.
- •В координатной форме
- •[Править]Обозначения
- •[Править]Свойства коллинеарности
- •Линейно зависимые и линейно независимые системы векторов
- •1.Двумя точками (а и в).
- •2. Двумя плоскостями (; ).
- •3. Двумя проекциями.
- •Уравнение прямой по точке и вектору нормали
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой по точке и угловому коэффициенту
- •Уравнение прямой по точке и направляющему вектору
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Угол между прямыми на плоскости
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •Расстояние от точки до прямой
- •Расстояние от точки до прямой
- •Угол между прямыми на плоскости
- •Уравнение плоскости
- •Угловой коэффициент в уравнении прямой. Геометрический смысл коэффициента.
- •Расстояние от точки до прямой
- •Взаимное расположение двух плоскостей (формулировки и примеры)
- •Угол между плоскостями
- •Прямая в пространстве
- •Числовые последовательности
- •Арифметические действия над числовыми последовательностями
- •Ограниченные и неограниченные последовательности
- •Бесконечно большие и бесконечно малые последовательности
- •Связь между бесконечно малыми и бесконечно большими последовательностями
- •Оновные свойства бесконечно малых последовательностей
- •Определения
- •[Править]Промежутки монотонности
- •[Править]Примеры
- •Способы определения
- •[Править]Свойства
- •Теорема о вложенных отрезках
- •Односторонний предел по Гейне
- •[Править]Односторонний предел по Коши
- •Теоремы о пределах
- •Второй замечательный предел
- •Исчисление бесконечно малых и больших
- •[Править]Бесконечно малая величина
- •[Править]Бесконечно большая величина
- •[Править]Свойства бесконечно малых
- •[Править]Сравнение бесконечно малых
- •[Править]Определения
- •[Править]Примеры сравнения
- •Определение непрерывности функции
- •Арифметические действия над непрерывными функциями
- •Определение
- •[Править]Существование
- •[Править]Примеры
- •[Править]Свойства
- •Понятие производной
- •Геометрический смысл производной
- •Производные и дифференциалы высших порядков
- •Дифференцируемость
- •[Править]Замечания
- •Дифференцирование функций, заданных параметрически
- •Следствие
- •Доказательство Лагранжа
- •Отношение бесконечно малых
- •[Править]Отношение бесконечно больших
- •Так почему же это является неопределённостью? Править
Определение
Функция ![]() является
обратной к функции
является
обратной к функции ![]() ,
если выполнены следующие тождества:
,
если выполнены следующие тождества:
f(g(y)) = y для всех
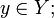
g(f(x)) = x для всех
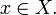
[Править]Существование
Чтобы найти обратную функцию, нужно решить уравнение x = F(y) относительно y. Если оно имеет более чем один корень, то функции обратной к F не существует. Таким образом, функция f(x) обратима на интервале (a;b) тогда и только тогда, когда на этом интервале она инъективна.
Для непрерывной
функции F(y) выразить y из
уравнения x − F(y)
= 0 возможно
в том и только том случае, когда
функция F(y) монотонна
(см. теорема
о неявной функции).
Тем не менее, непрерывную функцию всегда
можно обратить на промежутках её
монотонности. Например,
является
обратной функцией к x2 на ![]() ,
хотя на промежутке
,
хотя на промежутке ![]() обратная
функция другая:
обратная
функция другая: ![]() .
.
[Править]Примеры
Если
 ,
где a >
0, то F −
1(x)
= log ax.
,
где a >
0, то F −
1(x)
= log ax.Если
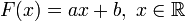 ,
где
,
где  фиксированные
постоянные и
фиксированные
постоянные и 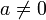 ,
то
,
то 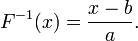
Если
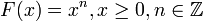 ,
то
,
то 
[Править]Свойства
Областью определения F − 1 является множество Y, а областью значений множество X.
По построению имеем:
![]()
или
![]() ,
,
![]() ,
,
или короче
![]() ,
,
![]() ,
,
где ![]() означает композицию
функций,
а idX,idY — тождественные
отображения на X и Y соответственно.
означает композицию
функций,
а idX,idY — тождественные
отображения на X и Y соответственно.
Функция F является обратной к F − 1:
![]() .
.
Пусть
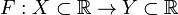 —
биекция. Пусть
—
биекция. Пусть 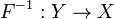 её
обратная функция.
Тогда графики функций y = F(x) и y = F −
1(x) симметричны
относительно прямой y = x.
её
обратная функция.
Тогда графики функций y = F(x) и y = F −
1(x) симметричны
относительно прямой y = x.Непрерывность обратной функции
Пусть
 --
функция, непрерывная на отрезке
--
функция, непрерывная на отрезке 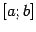 .
Предположим, что
монотонна
на
;
пусть, для определённости, она монотонно
возрастает: из
.
Предположим, что
монотонна
на
;
пусть, для определённости, она монотонно
возрастает: из  следует,
что
следует,
что 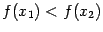 .
Тогда образом отрезка
будет
отрезок
.
Тогда образом отрезка
будет
отрезок 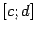 ,
где
,
где  и
и 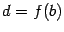 (действительно,
непрерывная функция принимает любое
промежуточное между
(действительно,
непрерывная функция принимает любое
промежуточное между 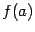 и
и  значение,
причём ровно один раз, что следует из
монотонности). Поэтому существует
обратная к
значение,
причём ровно один раз, что следует из
монотонности). Поэтому существует
обратная к  функция
функция 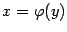 функция,
действующая из
в
.
Очевидно, что
функция,
действующая из
в
.
Очевидно, что 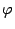 монотонно
возрастает. (Если бы функция
монотонно
возрастает. (Если бы функция  была
монотонно убывающей, то и обратная к
ней функция
тоже
была бы монотонно убывающей.)
была
монотонно убывающей, то и обратная к
ней функция
тоже
была бы монотонно убывающей.)Теорема 3.11 Пусть -- непрерывная монотонная функция,
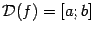 ,
,  .
Тогда обратная к
функция
непрерывна
на отрезке
.
.
Тогда обратная к
функция
непрерывна
на отрезке
.Доказательство. Во-первых, заметим, что если
 ,
,  ,
то
,
то  .
.Во-вторых, пусть
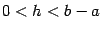 ;
рассмотрим функцию
;
рассмотрим функцию  ,
которая определена при
,
которая определена при 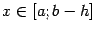 .
Очевидно, что
.
Очевидно, что 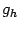 --
непрерывная на
--
непрерывная на  функция,
поэтому она принимает наименьшее
значение
функция,
поэтому она принимает наименьшее
значение 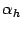 в
некоторой точке
в
некоторой точке 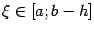 :
:
Таким образом, если
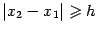 ,
то
,
то 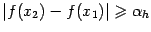 ,
то есть если
,
то есть если 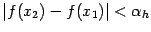 ,
то
,
то  .
Последнее утверждение можно
переформулировать так: для любого
числа
.
Последнее утверждение можно
переформулировать так: для любого
числа 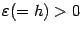 найдётся
число
найдётся
число  ,
такое что при
,
такое что при  выполняется
неравенство
выполняется
неравенство 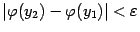 .
(При этом
.
(При этом  ,
, 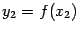 ,
, 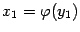 ,
,  .)
Получили, что функция
удовлетворяет
определению равномерной непрерывности
на отрезке
;
тем самым доказано утверждение теоремы.
.)
Получили, что функция
удовлетворяет
определению равномерной непрерывности
на отрезке
;
тем самым доказано утверждение теоремы.
Билет 38.
Понятие производной
Рассмотрим задачу, которая приводит к понятию производной. Пусть функция u(t) выражает количество произведенной продукции за время t. Найдем производительность труда в момент t0. За период от t0 до t0+D t количество продукции изменится от u(t0) до u0+D u = u(t0+D t). Тогда средняя производительность труда за этот период z = D u/D t, поэтому производительность труда в момент t0
z = limD t® 0D u/D t.
Определение 1 (производная). Производной функции y = f(x) в фиксированной точке x называется предел
limD x® 0D y/D x
при условии существования этого предела.
Производная обозначается следующим образом f'(x) или y'.
Пример 1. Вычислить производную функции y = sin x. Найдем приращение функции:
D y = sin(x+D x)-sin x = 2sin(D x/2) cos (x+D x/2).
По определению производной
(sin x)' = limD x® 0D y/D x = limD x® 0(cos (x+D x/2)(sin D x/2)/(D x/2)) = =cos x,
так как
limD x® 0cos (x+D x/2) = cos x.
Таким образом,
(sin x)' = cos x.
Определение 2. Правой (левой) производной называется правый (левый) предел
limD x® 0 + 0D y/D x
limD x® 0 - 0D y/D x ,
если эти пределы существуют.
Для обозначения правой (левой) производной используют символ: f'(x+0) f'(x-0). Необходимым и достаточным условием существования производной является равенство f'(x+0) = f'(x-0).
Пример 2. Доказать, что f(x) = 3|x|+1 не имеет производной в точке x = 0. Составим D y = 3(0+D x)+1-1=3D x при D x>0. При D x<0 D y = -3(0+D x)+1-1=-3D x, значит,
limD x® 0-0D y/D x =-3, limD x® 0+0D y/D x = 3.
Поэтому данная функция не имеет производной в точке x = 0.
