Числовые последовательности

      Если каждому числу n из натурального ряда чисел: 1, 2, 3, …, n, … поставлено в соответствие вещественное число x_n, то множество вещественных чисел x₁, x₂, …,x_n, … называется числовой последовательностью или просто последовательностью.   Числа x₁, x₂, x₃, …, x_n,… будем называть элементами (или членами) последовательности, x_n = f (n) – формула, по которой находится каждый член последовательности, называется общим членом последовательности. Сокращенно последовательность будем обозначать символом { x_n }   Примеры числовых последовательностей

• 1)  

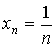
• 2)  

• 3)  a_n = a₁ + (n - 1)·d – арифметическая прогрессия,

• 4)  x_n = x₁·q^{n - 1}– геометрическая прогрессия,

• 5)  x_n = τ (n) – число делителей числа n,

• 6)   x_n = n !

  Последовательность считается заданной, если указан способ получения любого ее элемента. Последовательность можно задать соотношением между двумя последовательными членами последовательности. К примеру, арифметическую прогрессию можно задать соотношением a_n = a_n-1 + d, начиная со второго члена. По самому определению, последовательность содержит бесконечное число элементов, любые два ее элемента отличаются, по крайней мере, своими номерами.

Арифметические действия над числовыми последовательностями

  Пусть даны последовательности {x_n} и {y_n}.

• Произведением последовательности {х_n} на число m назовем последовательность m·x₁, m·x₂, …, m·x_n, ….

• Суммой данных последовательностей назовем последовательность x₁ + y₁, x₂ + y₂, …, x_n + y_n, ….

• Разностью – последовательность x₁ − y₁, x₂− y₂, …, x_n− y_n, …,

• Произведением — последовательность x₁·y₁, x₂·y₂, … x_n·y_n,…

• Частным — последовательность   если все члены последовательности {y_n} отличны от нуля.

  Указанные действия над последовательностями символически записываются так:

• –     m·{ x_n} = {m· x_n}

• –    { x_n} + { y_n} = { x_n + y_n}

• –  { x_n} - { y_n} = { x_n - y_n}

• –  { x_n} · { y_n} = { x_n · y_n}

• –   если y_n ≠ 0.

Ограниченные и неограниченные последовательности

      Числовая последовательность {х_n} называется ограниченной, если существуют числа m и M, такие, что любой элемент x_n этой последовательности удовлетворяет неравенствам

m ≤ x_n ≤ M.

      Пусть А = max{ | m |, | M |}. Тогда условие ограниченности последовательности можно записать в виде | x_n | ≤ А   n ≥ N:

   Здесь и в дальнейшем будем пользоваться квантором всеобщности   и квантором существования  . Не вдаваясь в подробности определения этих логических операций, будем читать квантором всеобщности   как "для любого", а квантор существования   как "существует".   Последовательность {х_n} называется неограниченной, если для любого как угодно большого положительного числа А существует элемент x_n этой последовательности, удовлетворяющий неравенству | x_n | > A, (т.е. либо x_n > A, либо x_n < - A):

  Последовательность ограничена сверху, если все ее элементы принадлежат промежутку ( - ∞, M]:

  Последовательность ограничена снизу, если все ее элементы принадлежат промежутку [m, + ∞):

   З а м е ч а н и е. Неограниченная последовательность может быть ограничена сверху (снизу).   Сравнивая запись с помощью логических символов двух последних определений, видим, что при построении отрицаний символы   и   заменяют друг друга и неравенства меняют свой смысл.

Билет 24.