Алгоритм Описание
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.
Система линейных уравнений:
Определители:
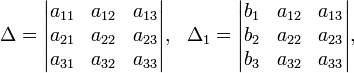
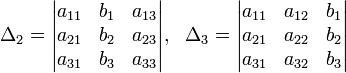
Решение:
Обратная матрица
С помощью матрицы алгебраических дополнений
Матрица 2х2
Обращение
матрицы 2х2 возможно только при условии,
что 
.
Билет 7.
Линейные операции над векторами
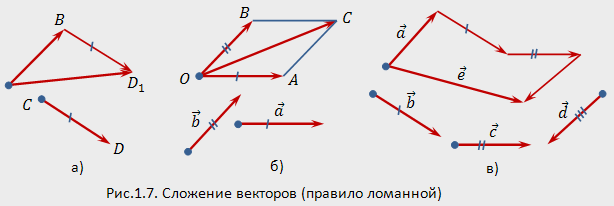
Сложение векторов
Пусть
даны два вектора 
и 
.
Приложим вектор
к
точке 
(концу
вектора
)
и получим вектор 
(рис.1.7,а;
здесь и далее равные векторы отмечены
одинаковыми засечками).
Вектор 
называется суммой
векторов
и
и
обозначается 
.
Это нахождение суммы называется правилом
треугольника.
Сумму
двух неколлинеарных векторов 
и 
можно
найти по правилу
параллелограмма.
Для этого откладываем от любой
точки 
векторы 
и 
,
а затем строим параллелограмм 
(рис.
1.7,6). Диагональ 
параллелограмма
определяет сумму: 
.
Для
нахождения суммы нескольких векторов
можно построить ломаную из равных им
векторов. Тогда замыкающий
вектор,
соединяющий начало первого вектора
ломаной с концом последнего ее вектора,
равен сумме всех векторов ломаной. На
рис.1.7,в изображена сумма 
четырех
векторов 
.
Таким способом (правило
ломаной)
можно сложить любое конечное число
векторов. Заметим, что сумма векторов
не зависит от точек приложения слагаемых
и от порядка суммирования. Например,
"выстраивая цепочку" векторов для
суммы в виде 
,
получим вектор, равный вектору 
.
Если ломаная получилась замкнутой, то
сумма равна нулевому вектору.
