
- •1. Матрицы. Виды матриц
- •Специальные матрицы
- •2. Разложение Тейлора. Формула Тейлора с остаточным членом в форме Пеано.
- •Теорема о необходимых условиях экстремума
- •1) Перестановка любых 2ух уравнений местами
- •3) Умножение обоих частей в каком-либо ур-ии слу на число 0
- •4) Прибавление к какому-либо из уравнению слу др уравнения этой же слу, умноженного на произвольное число 0.
- •2) Если │а│0, то решение может быть найдено по формуле:
- •2 Слу наз эквивалентными или равносильными, если множества их решений совпадают.
- •Теорема об умножении определителей
- •2. Разложение Тейлора. Формула Тейлора с остаточным членом в форме Пеано.
- •Теорема о необходимых условиях экстремума
- •Ранг матрицы r(a) – это наивысший порядок отличных от 0 миноров этой матрицы
- •Теорема о производной по направлению
- •Теорема о необходимых условиях экстремума
- •2) Пусть противоречивых уравнений нет. Тогда 1 из уравнений выбирается за разрешающее уравнение и одно из неизвестных – за разрешающее неизвестное. К этому выбору предъявляются следующие требования:
- •3) Разрешающая неизвестная исключается из всех уравнений кроме разрешающего. Для этого разрешающее уравнение прибавляется к каждому из уравнений слу после умножения на подходящее число.
- •1) Реализация метода Гаусса даёт ответ на вопрос о совместности системы. Система совместна тогда и только тогда, когда при реализации метода Гаусса не возникает противоречивых уравнений
- •2) В процессе преобразований Гаусса допускаются промежуточные преобразования слу.
- •3) В любой момент преобразования Гаусса м.Б. Остановлены. Текущая система м.Б. Рассмотрена в качестве исходной и преобразования м.Б. Возобновлены по другой схеме.
- •1. Алгебраическое дополнение и минор
- •Теорема о необходимых условиях экстремума
- •2) Проводится подстановка любой точки, не лежащей на критической прямой, в текущее неравенство, тем самым определяется область «хороших» и «плохих» точек.
- •3) После выявления «хороших» полупространств для каждого неравенства производится их пересечение.
- •2) Если │а│0, то решение может быть найдено по формуле:
- •1. Понятие множества уровня функции, касательной гиперплоскости и вектора нормали к гиперплоскости.
- •1. Методы поиска обратной матрицы: метод союзной матрицы и метод элементарных преобразований.
- •2) Система s линейно-независима
- •2) Любой вектор yRn м.Б. Представлен в виде линейной комбинации векторов системы s
- •2. Экономическая интерпретация двойственных оценок
- •Метод окаймляющих миноров
- •Метод элементарных преобразований
- •Теорема об обратной матрице
- •64 Теорема о разрешимости тз:
- •1) Перестановка любых 2ух уравнений местами
- •3) Умножение обоих частей в каком-либо ур-ии слу на число 0
- •4) Прибавление к какому-либо из уравнению слу др уравнения этой же слу, умноженного на произвольное число 0.
- •2. Двойственные злп.
- •1) Перестановка любых 2ух уравнений местами
- •3) Умножение обоих частей в каком-либо ур-ии слу на число 0
- •4) Прибавление к какому-либо из уравнению слу др уравнения этой же слу, умноженного на произвольное число 0.
- •2) Пусть противоречивых уравнений нет. Тогда 1 из уравнений выбирается за разрешающее уравнение и одно из неизвестных – за разрешающее неизвестное. К этому выбору предъявляются следующие требования:
- •3) Разрешающая неизвестная исключается из всех уравнений кроме разрешающего. Для этого разрешающее уравнение прибавляется к каждому из уравнений слу после умножения на подходящее число.
- •1. Назначение и обоснование обобщенного метода множителей Лагранжа.
- •2. Открытая транспортная задача на избыток
- •26.Понятие градиента функции. Теорема о градиенте.
- •Методы поиска обратной матрицы: метод союзной матрицы и метод элементарных преобразований.
- •1. Ранг матрицы r(a) – это наивысший порядок отличных от 0 миноров этой матрицы
- •Метод окаймляющих миноров
- •Метод элементарных преобразований
Ранг матрицы r(a) – это наивысший порядок отличных от 0 миноров этой матрицы
Ранг матрицы тесно связан с понятием линейной независимости строк (столбцов) матрицы. Рассмотрим произвольную матрицу А. Обозначим через Аj – j-ый столбец матрицы А.
Рассмотрим систему S={Ai1, Ai2, …, Aik} – набор столбцов матрицы А.
Система столбцов S матрицы А, наз линейно-зависимой, если существует набор чисел 12…k среди кот есть отличные от 0, такой, что j=1kjAij=0
Столбцы, входящие в систему S, наз-ся линейно-зависимыми.
В случае, когда набора чисел 12…k при кот выполняется последнее соотношение не существует, то тогда система S наз линейно-независимой.
Выражение L=j=1kjAij=1 Ai1 + 2 Ai2 + … + k Aik стоящее в левой части первого выражения наз-ся линейной комбинацией столбцов системы S.
Система столбцов S матрицы А наз базисом системы всех столбцов матрицы А, если:
1) система S линейно-независима
2) любой столбец матрицы А может быть представлен в след виде линейной комбинации столбцов системы S, т.е. для каждого р=1, n
Аp = j=1kjp Aip
Аналогично определяются понятия линейной зависимости-независимости строк матрицы, базиса в системе строк.
Любой отличный от 0 минор матрицы, порядок которого равен рангу этой матрицы наз её базисным минором
Теорема о ранге (базисном миноре)
Ранг матрицы равен максимальному числу линейно-независимых ее столбцов (строк), при этом система столбцов (строк) матрицы, содержащая базисный минор образует базис системе всех столбцов (строк) матрицы
2.
|
прямая ЗЛП: |
|
двойственная ЗЛП: |
|
|
|
|
Нетрудно видеть, что если задачу (14.3)-(14.4) взять за прямую, то двойственной по отношению к ней будет задача (14.1)-(14.2). В связи с эти говорят, что задачи (14.1)-(14.2) и (14.3)-(14.4) образуют так называемую двойственную пару ЗЛП.
Двойственная
лемма. Для
любого плана
![]() задачи
(14.1)-(14.2) и любого плана
задачи
(14.1)-(14.2) и любого плана
![]() задачи (14.3)-(14.4)
справедливо
задачи (14.3)-(14.4)
справедливо
![]() .
.
Доказательство.
Умножим
основное ограничение
![]() задачи (14.1)-(14.2) на
задачи (14.1)-(14.2) на
![]() слева:
слева:
![]() . (14.5)
. (14.5)
Умножим основное
ограничение
![]() задачи (14.3)-(14.4) на
задачи (14.3)-(14.4) на
![]() слева:
слева:
![]() (14.6)
(14.6)
Преобразуем левую часть (14.5), используя свойства операции транспонирования:
![]() (14.7)
(14.7)
Из (14.7) следует, что
левые части (14.5) и (14.6) равны между собой.
Это означает, что
![]() что и требовалось доказать.
что и требовалось доказать.
Следствие.
Если для
некоторых планов
![]() и
и
![]() задач двойственной пары (4.25)-(4.26)
и
(4.27)-(4.28)
задач двойственной пары (4.25)-(4.26)
и
(4.27)-(4.28)
![]() то эти планы являются оптимальными
планами своих задач.
то эти планы являются оптимальными
планами своих задач.
Компоненты
![]() оптимального плана двойственной ЗЛП
(14.3)-(14.4) называются двойственными
оценками.
Двойственные оценки играют в линейном
программировании ту же роль, что и
множители Лагранжа в нелинейном
программировании.
оптимального плана двойственной ЗЛП
(14.3)-(14.4) называются двойственными
оценками.
Двойственные оценки играют в линейном
программировании ту же роль, что и
множители Лагранжа в нелинейном
программировании.
Компоненты
![]() оптимального плана прямой ЗЛП (14.1)-(14.2)
называются прямыми
оценками
оптимального плана прямой ЗЛП (14.1)-(14.2)
называются прямыми
оценками
БИЛЕТ 17
1. Алгебра СМ
Шаг 0 (поиск опорного плана):
Опорный план задачи f(x)=ctx) → max;(1) {Ax=b,x>=0}(2) м б найден путем решения СЛУ Ax=b ограничений (2), мнтодо Гауса. Без ограничения общности можно считать, что базисными переменными будут первые m переменных, которые могут быть выражены через оставшиеся свободными переменными след образом:
xi=βi-Σj=m+1 αijxj , i=1,m (3)
Все βi в (3) должны быть неотрицательными, если это не так, то СЛУ перерешивается методом Гаусса относительно другого состава базисных перем., и так до тех пор пока, пока все βi в (3) не будут неотрицат. Согласно теореме о вершине, точка xt(1)=( β1, β2,…, βm, 0,…) является вершиной, т. к. все своб. перемен. равны 0.
Шаг 1 (выражение эл-тов текущей задачи через своб. перем.):
Подставляя (3) в выражение (1) получаем:
f(x)= ctx= Σi=1n cixi=Σi=1m cixi + Σj=m+1n cixj= Σi=1m ci(βi- Σj=m+1n αijxj) + Σj=m+1n cixi= Σi=1m ci βi - Σj=m+1n Δjxj (4) ,где Δj=Σi=1m ciαij – cj (5 )
Т.о целевая ф-ия зависит лишь от свободных переменных.
f(x)= f0 –- Σj=m+1n Δjxj (6)
f0= Σi=1m ci βi=cбtP0 (7)
Δj= cбtPj – cj (8)
где P0т=β1, β2, ..., βm) – вектор правой части,
Pjт=(α1j, α2j, …, αmj) – j-тый столбец м-цы
сбт=(с1, с2, …, сm) – вектор, состоящ. из коэф-тов при базисных переменных в выражении для целевой функции.
Исходная задача принимает вид: f(x)=f0-Σj=m+1n Δjxj → max (9)
Шаг 2 (поиск возможных переходов):
Ищем вершину, на кот. значение целев. ф-ции > чем на х(1) Возможны варианты:
а) Все Δj в (9) меньше 0 или равны 0. В этом случае т. Х(1) является
оптим. планом, поскольку любые изменения своб. переменных не увеличивают значение целевой ф-ции.
б) Существует хотя бы одно Δk<0. Тогда значение целев. ф-ции можно увеличить за счёт своб. переменной хk, изначально равной 0.
Шаг 3 (переход к новой вершине):
Увеличим переменную хk, оставляя все другие своб. перем. равными 0. Предел увеличения устанавливается из условия неотрицательности всех баз-х перем. , кот., как следует из (3) будут изменятся по закону: xi = βi - αikxk
Условие неотрицательности даёт: xi = βi - αikxk ≥ 0, (12)
Возможны варианты:
а) Все αik ≤ 0. В этом случае все нерав-ва (12) останутся справедл. при любых больших значениях xk. Её можно увел. безгранично, решения нет, целевая ф-ция не ограничена сверху.
б) Одно или несколько αik > 0. Тогда каждая αik порождает границу для увеличения xk:
xk ≤ βi / αik = γi (13)
Пусть этот min γ достигается при i=r, т е γ=γr = min(βr / αrk ) (14)
Увеличим xk до предела, оставляя при этом все другие своб. переменные равными 0. По достижении верхней границы, перем xk обнуляет базис. перем. xr , кот. объявляется свободной, xk объявляется базисной. Тогда точка:
хт(2) =( β1, …, βr-1, 0, βr+1, …, βm, 0, 0, …, γk, 0 )
является вершиной области ограничения задачи. Далее переход на шаг ⁿ
2 Градиентом f(x) функции f(x) в точке z наз вектор, компонентами кот являются частные производные 1ого порядка функции Tf(x)=(f(x)/x1, f(x)/x2,… f(x)/xn)
БИЛЕТ 18
1. Постановка задачи нелинейного программирования (ЗНЛП) с ограничениями равенствами
Решается задача f(x)→ min (max) (1)
g1(x)=b1
g2(x)=b2 (2)
………
gm(x)=bm
Которая м.б. записана в виде
f(x)→min (max) (3)
g(x)=b (4) где g(x) – вектор функция ограничения исходной задачи, компонентами кот являются функции gi(x) (i=1,m) стоящие в левой части системы ограничений (2).
В общем случае f(x) и gi(x) являются нелинейными функциями.
Множество точек х, являющихся решением системы ограничений (2) задают область ограничений ДRn задач (1)-(2) и (3)-(4).
Сформулируем теорему, дающую достаточные условия существования решения ЗНЛП общего вида:
f(x)→ min (max) (5),
хД с Rn (6)
Теорема Вейерштрасса:
Пусть область ограничений Д, задачи (5)-(6) является не пустым и компактным множеством, тогда непрерывная целевая функция f(x),заданная на этом множестве, достигает глобального условного экстремума на внутренней или граничной точке множества Д.
Данная теорема справедлива для любых ЗНЛП в том числе и для задач с ограничениями-равенствами
2. Задача выпукло-вогнутого программирования мб решена методом Куна-Таккера.
Схема реализации метода:
-
Проверяются св-ва целевой ф-ции f(x) и устан-ся в соответствии с усл-ми табл. Если рез-ты положительны (усл-я табл выполнены), то переходим на 2 шаг.
-
Проверяется является ли обл-ть ограничений D выпуклым множеством.
-
Выписывается и решается система условий Куна-Таккера. Полученное решение явл-ся оптимальным планом исходной задачи.
Подходы к реш-ю плохо обусловленных задач нелинейного програм-я.
Если усл-я f(x)max(min) и x D не выполняются то применяют данный метод, придерживаясь след схемы:
Если возможно, то обл-ть ограничений D разбивается на подмн-ва, во всех точках которых целевая ф-ция дифференцируема, после чего можно применять привычные методы. Также обл-ть D можно разбить на мн-во, в которых целевая ф-ция непрерывна, после чего применить теорему Вейерштрасса
БИЛЕТ 19
1. Понятие производной по направлению. Теорема о производной по направлению.
Пусть URn,произвольный вектор единичной длины, т.е. U=1
Производной ф-ии f(x) в т. z по напр-ию вектора U наз величина
f(z)/U=limt0 (t>0) (f(z+tU)-f(z))/t
По сути f(z)/U – это скорость изменения функции f(x) в точке z по направлению вектора U

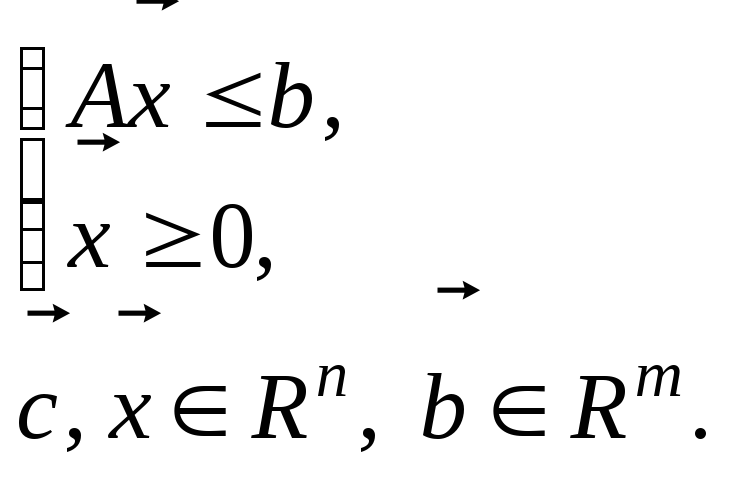 (14.2)
(14.2)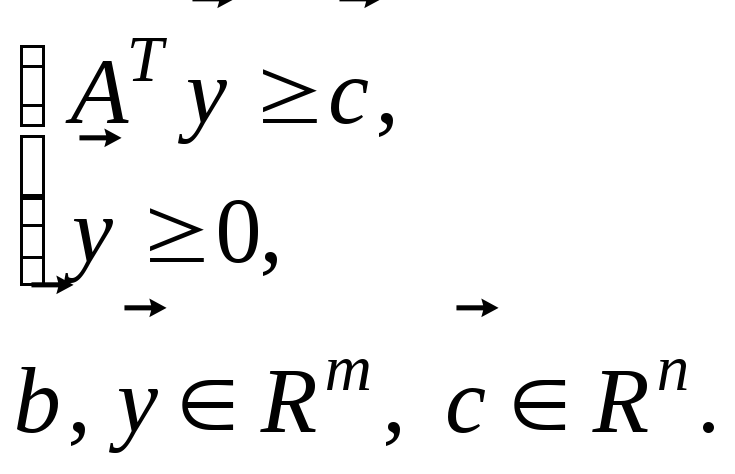 (14.4)
(14.4)