2. Разложение Тейлора. Формула Тейлора с остаточным членом в форме Пеано.

Пусть k^т = (k₁, k₂, … , k_m) – это вектор с целочисленными неотрицательными компонентами. Обозначим через [k] сумму его компонентов, т.е. [k] = k₁+ k₂+ … + k_m

Говорят, что функция φ₁(х) есть «О малое» по сравнению с φ₂(х) при х→0, если справедливо условие:

lim_x→0 (φ₁(х) / φ₂(х) ) = 0

Это соотношение означает, что φ₁(х) пренебрежительно мала по сравнению с φ₂(х) при х→0.

Расширенной записью этого является следующая: φ₁(х) = 0* (φ₂(х)). Это выражение означает, что φ₁ есть «О малое» по сравнению с φ₂.

Пусть f(x) - некоторая функция, где xRⁿ. Предположим, что эта функция дифференц-а в некоторой окрестности O_ в точке yRⁿ, причем имеет все частные производные вплоть до производных (m+1) порядка. Тогда справедлива формула Тейлора:

f(x)=_[k]=0^m 1/m! * (^[k]f(y)/x₁^k1x₂^k2…x_n^kn) * (x₁-y₁)^k1 (x₂-y₂)^k2… (x_n-y_n)^kn +0 (x-y^m) (1)

Величина 0(x-y^m) - остаточный член в форме Пеано.

Т.е. формула (1) есть разложение Тейлора функции f(x) в точке у с точностью до производных m-ого порядка с остаточным членом в форме Пеано.

В частности разложение Тейлора функции f(x) в точке y с точностью до производных 2ого порядка есть:

f(x)=f(y)+^Tf(y)(x-y)+1/2 * (x-y)^T H(y)(x-y)+0(x-y)² где H(y) – матрица Гессе ф-ии f(x) в точке y

В одномерном случае при n=1 формула Тейлора принимает вид:

f(x)=_k=0^m1/k! * f^[k](y)(x-y)^k + 0 (x-y)^m

БИЛЕТ 5

1. Назначение Схема реализации метода множителей Лагранжа.

В основе метода лежит тот факт, что в точке условного экстремума хД градиент целевой функции f(x) д.б. ортогонален касательной гиперплоскости к области ограничений Д, определяемый системой ограничений g₁(x)=b₁ или g(x)=b:

→max(min)

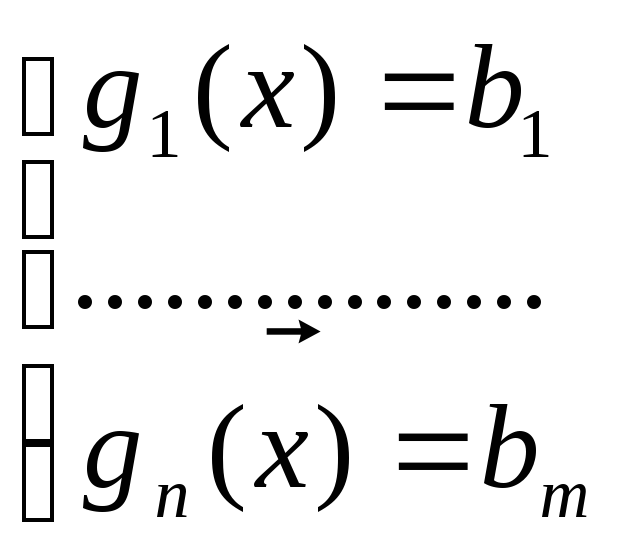
Это означает, что должны существовать такие числа ₁,₂,…_m для кот справедливо:

f(x) = _j=1ⁿ_j * g_j(x)

Метод реализуется выполнением следующих шагов:

Шаг1. Рассматривается ф-ия Лагранжа

L(x,λ) = f(x) + λ^T(b – g(x)) = f(x) + _i=1ⁿ _j (b_i – g_i(x))

Где x^T = (x₁, x₂, …, x_n) – вектор инструментальных переменных множителей Лагранжа,

λ^T = (λ₁, λ₂, … , λ_m) – вектор множителей Лагранжа.

Шаг2. Определяются стационарные точки (х^*, λ^*) функции множителей Лагранжа. Для этого решается система уравнений, представляющая собой необходимые условия существования стационарной точки (все частные производные по аргументам функции Лагранжа равны 0)

∂L(x,λ) / ∂x_j = (∂f(x) / ∂x_j) - _i=1^m λ_i * (∂g_i(x) / ∂ x_j) = 0, j = 1, m

∂L / ∂ λ_i = b_i - g_i(x) = 0, i = 1, m

Эта система м.б. представлена в матричной форме:

f_х(x) - λ^T Rg(x) = 0

b – g(x) = 0

где Rg(x) – матрица Якоби вектор-функции g(x)

2. Двойственные ЗЛП.

Каждой ЗЛП можно поставить в соответствие другую ЗЛП, кот. называется двойственной по отношению к исходной в симметричной форме:

Прямая ЗЛП: Двойственная ЗЛП:

f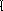(x) = c^тx → max(1) g(y) = b^тy → min(3)

Ax ≤ b (2) A^тy ≥ c(4)

x ≥ 0 y ≥ 0

c, x Є Rⁿ, b Є R^m b, y Є R^m, c Є Rⁿ

Эти задачи образуют двойственную пару ЗЛП.

БИЛЕТ 6

1. .Условия Куна-Таккера. Теорема Куна-Таккера. Условия дополняющей нежесткости.

Условия Куна-Таккера, позволяющие идентифицировать стационарные точки в задаче-→max(min), gi(x)  0. Указанные условия являются необходимыми, однако оказываются также и достаточными, если целевая функция и функции ограничений обладают некоторыми специальными свойствами.

Теорема Куна-Таккера:

Необх-ми усл-ми сущ-ия стацин-й т. ф-ии Лагранжа ,явл-ся след-е усл-ия:

Эти усл-ия м.б. записаны в алгебраической форме:

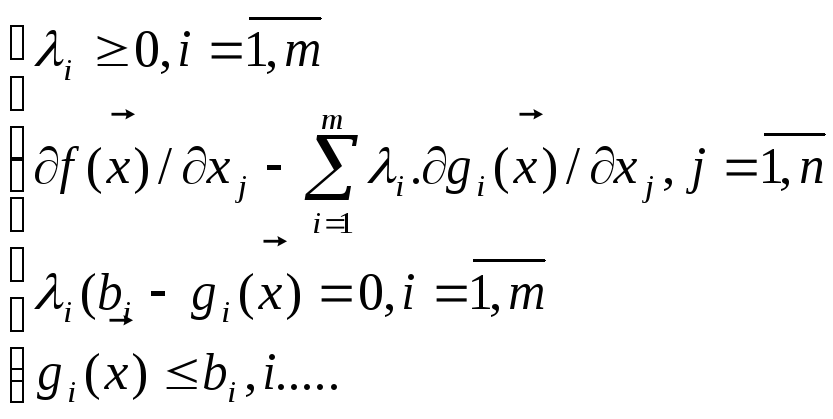
Замечание:

Из 1 и 3 (в системе) усл-й К-Т след-ет, что либо множ-ль Лагранжа =0, либо соответсвующее огр-ие вып-ся как строгое равенство, либо то и др-е вып-ся одноврем-но

2. Схем реализ. графич. метода:

Шаг 1: графич. способом строится обл. огр. D ЗЛП.

Шаг 2: строится направляющий вектор с = градf, как направленный отрезок соединяющий точку начала координат с точкой с.

Шаг 3: через любую точку области D проводится плоскость(прямая), ортогональная вектору с.

Шаг 4: построенная на шаге 3 плоскость перемещается в направлении вектора с параллельно самой себе до точки последнего соприкосновения перемещаемой плоскости (прямой) с областью D. Точка отрыва определяет оптимальный план задачи.

Шаг 5: Устанавливаютя точные значения компонент оптим плана для чего решантся система уравнений, определяющих те прямые в рез-те пересечения которых возникает точка оптимального плана.

БИЛЕТ 7

1. 44Теорема Каратеодори:

Пусть x(1), x(2),…,x(N) – вершины выпуклого многогранника D, тогда любая т. xЄD этого многогранника может быть представлена в виде выпуклой линейной комбинации его вершин

x=Σ_j=1^N λ_jx(j), где Σ_j=1^N λ_j=1, λ_j≥0, j=1,N

Теорема о решении ЗЛП:

Пусть D есть обл. ограничений ЗЛП, тогда справедливо следующее:

1. Оптимальный план ЗЛП достигается в одной или нескольких вершинах обл огранич D.

2. Если онтимальный план достигается сразу в нескольких вершинах, то любая выпуклая линейная комбинация этих вершин так же явл-ся оптимальным планом.

Теорема о вершине:

Для того, чтобы т. x была вершиной обл. ограничений ЗЛП в канон. форме представления f(x) → max (min), x>0 Ax=b(система), необходимо и достаточно чтобы эта т. была решением СЛУ Ax=b, в кот. все свободные переменные =0, а базисные неотрицательны.

Следствие:

Число положит. компонент вершины обл. ограничений x>0 Ax=b(система) не может быть >m, где m число уравнений в системе Ax=b

2. Теорема об условиях определённости матрицы.

Справедливы утверждения:

1)квадратная матрица положительно определена <=> когда все ее главные (угловые) миноры положительны

2) квадратная матрица отрицательно определена <=> когда знак любого ее главного (углового) минора каждого порядка совпадает со знаком (-1)^К

Классический метод поиска безусловного экстремума функции является методом решения ЗНЛП простейшего класса – ЗНЛП без ограничений:

В основе метода лежат сформулированные выше теоремы о необходимых и достаточных условиях существования безусловного экстремума. Метод применим только для "достаточно гладких" (дважды непрерывно дифференцируемых функций). Метод состоит в выполнении следующих шагов.

Шаг 1. Решить уравнение (или систему уравнений ) и найти множество ее решений – стационарных точек (подозрительных на экстремум).

Шаг 2. Установить, пользуясь теоремой об условиях определенности матрицы, тип определенности матрицы Гессе в каждой стационарной точке функции , и на основе этого сделать вывод о существовании и типе экстремума

БИЛЕТ 8

1.Теорема о необходимых условиях экстремума. Теорема о достаточных условиях экстремума. Теорема об условиях определенности матрицы (Критерий Сильвестра)