Метод окаймляющих миноров

Пусть некоторый минор матрицы k-ого порядка М_k0, тогда ранг этой матрицы по меньшей мере равен k, т.е. r(A)  k . Рассмотрим все окаймляющие (содержащие в себе минор М_k) миноры k+1 порядка. Если все они равны 0, то значит ранг матрицы равен k, но если найдётся хотя бы один M_k+10, тогда процедура повторяется снова

Метод элементарных преобразований

Основан на том, что элементарные преобразования не изменяют ранга матрицы. Метод заключается в осуществлении последовательности элементарных преобразований над строками (столбцами) исходной матрицы. В результате все элементы вне главной диагонали становятся равными нулю, за исключением первых S элементов главной диагонали. Следовательно, ранг матрицы равен S.

Св-ва ранга

1) 0≤ r(A)  min {m,n}

2) r(AВ)  min {r(A) r(В) }

3) r(A) = r(A^T)= r(AА^т)

4) r(A+В) ≤ r(A) + r(В)

5) ранг произведений некоторой матрицы А слева или справа на невырожденную матрицу подходящего размера равен рангу исходной матрицы. r(AВ)= r(СA) , │В│≠ 0, │С│≠ 0

2. Условия Куна-Таккера. Теорема Куна-Таккера. Условия дополняющей нежесткости.

Условия Куна-Таккера, позволяющие идентифицировать стационарные точки в задаче-→max(min), gi(x)  0. Указанные условия являются необходимыми, однако оказываются также и достаточными, если целевая функция и функции ограничений обладают некоторыми специальными свойствами.

Теорема Куна-Таккера:

Необх-ми усл-ми сущ-ия стацин-й т. ф-ии Лагранжа ,явл-ся след-е усл-ия:

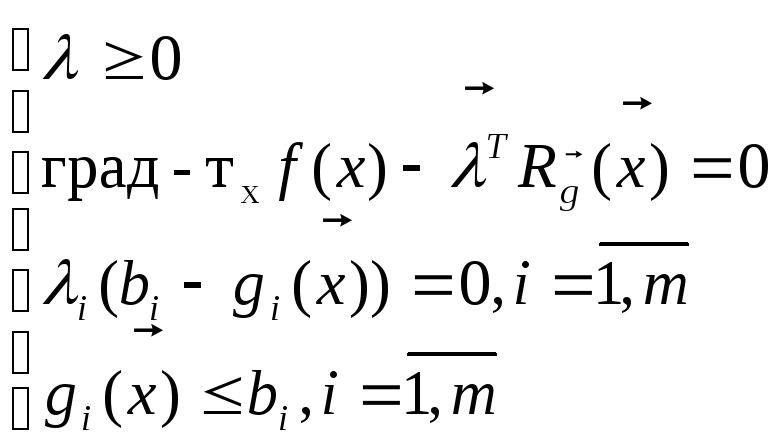
Эти усл-ия м.б. записаны в алгебраической форме:

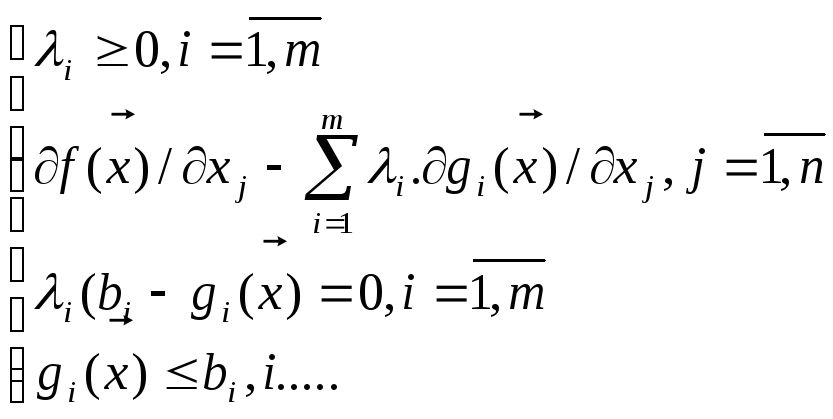
Замечание:

Из 1 и 3 (в системе) усл-й К-Т след-ет, что либо множ-ль Лагранжа =0, либо соответсвующее огр-ие вып-ся как строгое равенство, либо то и др-е вып-ся одноврем-но.

БИЛЕТ 36

1. Понятие обратной матрицы. Теорема об обратной матрице

Пусть задана квадратная матрица А_n*n. Матрица В_n*n такая, что А*В=В*А=Е наз обратной к матрице А и обозначается А^-1

А^-1 *А=А*А^-1 =Е

Теорема об обратной матрице

Справедливы утверждения:

1) Матрица А имеет обратную матрицу тогда и только тогда, когда определитель матрицы А не равен 0 (А0)

2) Если обратная матрица существует, то она единственна и ее можно найти по формуле:

А^-1= (1/А)*А^*

Где А^* является союзной матрицей и определяется по формуле

А^*=(А_ij)^т, т.е. элементами союзной матрицы являются элементы транспонированной матрицы алгебраических дополнений

По теореме о связи минора и алгебраических дополнений обратная матрица равна

А^-1=(1/А)*((-1)^i+jM_ij)^т

2. Закрытая ТЗ..

Имеется m поставщиков A₁, A₂, …, A_m некоторого однородного груза с запасами a₁, a₂, …, a_m.

Имеется n потребителей B₁, B₂, …, B_n с потребностями b₁, b₂, …, b_n соответственно.

Известны так же тарифы перевозок: c_ij, i = 1, m , j = 1,n

означающие стоимость перевозок единицы груза от A_i к B_j. Требуется составит план перевозок так, чтобы:

1. Суммарная стоимость всех перевозок была бы минимальной.

2. Каждый поставщик полностью реализует свой запас.

3. Каждый потребитель полностью удовл. свои потребности.

Формальная запись задачи:

f = Σ_i=1^mΣ_j=1ⁿ c_ijx_ij → min (1)

Σ_i=1^m x_ij = b_j , j = 1, n

Σ_j=1ⁿ x_ij = a_i , i = 1, m (2)

x_ij ≥ 0

_______________________________________________________