2) Проводится подстановка любой точки, не лежащей на критической прямой, в текущее неравенство, тем самым определяется область «хороших» и «плохих» точек.

3) После выявления «хороших» полупространств для каждого неравенства производится их пересечение.

БИЛЕТ 26

1. Понятие выпуклого множества. Теорема о пересечении выпуклых множеств. Понятие гиперплоскости в Rⁿ. Понятие полупространства.

Множество точек n-мерного пространства содержащие все точки отрезка соединяющего любые 2 точки этого множества наз выпуклым множеством

Теорема о пересечении выпуклых множеств

Пересечение любого числа выпуклых множеств явл выпуклым множеством.

Множество точек xRⁿ удовлетворяющих условию c^Tx=, где Rⁿ –где R¹ cRⁿ , наз гиперплоскостью в n-мерном пространстве

Уравнение c^Tx= наз уравнением гиперплоскости

Теорема о разделяющей гиперплоскости

Любая гиперплоскость разделяет все пр-во Rⁿ на 2 непересекающихся множества p₁ и p₂, наз полупространствами: p₁={xRⁿ:c^Tx}, p₂={xRⁿ:c^Tx>}

2. Назначение Схема реализации метода множителей Лагранжа.

В основе метода лежит тот факт, что в точке условного экстремума хД градиент целевой функции f(x) д.б. ортогонален касательной гиперплоскости к области ограничений Д, определяемый системой ограничений g₁(x)=b₁ или g(x)=b:

→max(min)

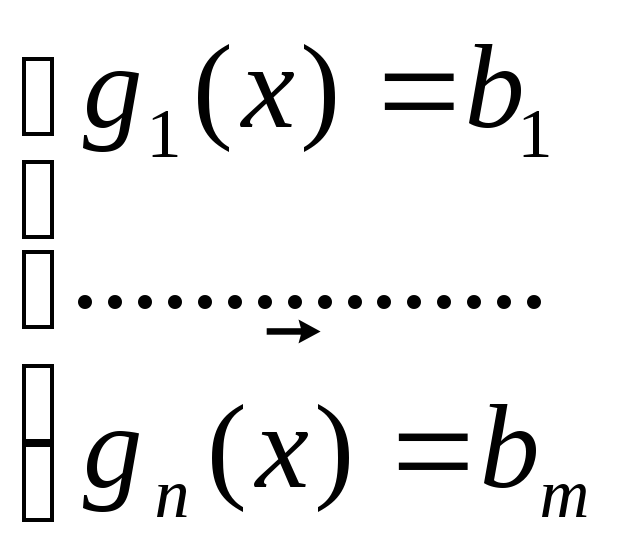
Это означает, что должны существовать такие числа ₁,₂,…_m для кот справедливо:

f(x) = _j=1ⁿ_j * g_j(x)

Метод реализуется выполнением следующих шагов:

Шаг1. Рассматривается ф-ия Лагранжа

L(x,λ) = f(x) + λ^T(b – g(x)) = f(x) + _i=1ⁿ _j (b_i – g_i(x))

Где x^T = (x₁, x₂, …, x_n) – вектор инструментальных переменных множителей Лагранжа,

λ^T = (λ₁, λ₂, … , λ_m) – вектор множителей Лагранжа.

Шаг2. Определяются стационарные точки (х^*, λ^*) функции множителей Лагранжа. Для этого решается система уравнений, представляющая собой необходимые условия существования стационарной точки (все частные производные по аргументам функции Лагранжа равны 0)

∂L(x,λ) / ∂x_j = (∂f(x) / ∂x_j) - _i=1^m λ_i * (∂g_i(x) / ∂ x_j) = 0, j = 1, m

∂L / ∂ λ_i = b_i - g_i(x) = 0, i = 1, m

Эта система м.б. представлена в матричной форме:

f_х(x) - λ^T Rg(x) = 0

b – g(x) = 0

где Rg(x) – матрица Якоби вектор-функции g(x)

БИЛЕТ 27

3. 1. Назначение Схема реализации метода множителей Лагранжа.

В основе метода лежит тот факт, что в точке условного экстремума хД градиент целевой функции f(x) д.б. ортогонален касательной гиперплоскости к области ограничений Д, определяемый системой ограничений g₁(x)=b₁ или g(x)=b:

→max(min)

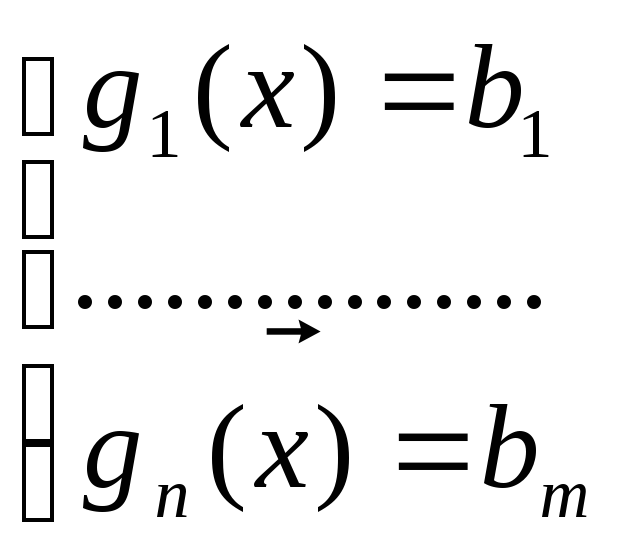
Это означает, что должны существовать такие числа ₁,₂,…_m для кот справедливо:

f(x) = _j=1ⁿ_j * g_j(x)

Метод реализуется выполнением следующих шагов:

Шаг1. Рассматривается ф-ия Лагранжа

L(x,λ) = f(x) + λ^T(b – g(x)) = f(x) + _i=1ⁿ _j (b_i – g_i(x))

Где x^T = (x₁, x₂, …, x_n) – вектор инструментальных переменных множителей Лагранжа,

λ^T = (λ₁, λ₂, … , λ_m) – вектор множителей Лагранжа.

Шаг2. Определяются стационарные точки (х^*, λ^*) функции множителей Лагранжа. Для этого решается система уравнений, представляющая собой необходимые условия существования стационарной точки (все частные производные по аргументам функции Лагранжа равны 0)

∂L(x,λ) / ∂x_j = (∂f(x) / ∂x_j) - _i=1^m λ_i * (∂g_i(x) / ∂ x_j) = 0, j = 1, m

∂L / ∂ λ_i = b_i - g_i(x) = 0, i = 1, m

Эта система м.б. представлена в матричной форме:

f_х(x) - λ^T Rg(x) = 0

b – g(x) = 0

где Rg(x) – матрица Якоби вектор-функции g(x)

2. Метод Крамера решения СЛУ

Этот метод предназначен для решения СЛУ в которых количество уравнений равно числу неизвестных т.е. матрица-система является квадратной.

Метод применяется только для тех СЛУ, где определитель не равен 0.

В основе метода лежит теорема Крамера:

Справедливы утверждения:

1) СЛУ Ах=b имеет единственное решение тогда и только тогда, когда │А│0