Теорема о необходимых условиях экстремума

Пусть функция f(x) имеет в точке x^* экстремум, тогда все ее частные производныеые первого порядка в этой точке равны 0, т.е. x^*является стационарной точкой:

f(x^*)/x_i = f ’x_i = 0,

Это соотношение эквивалентно f(x^*)=0

Теорема о достаточных условиях экстремума.

Пусть функция f(x) имеет непрерывные производные 2-го порядка в стационарной точке x^*, тогда точка x^* является точкой мах, если матрица Гессе Н(x^*) функции f(x) в т. x^* отрицательно определена, и точкой min,если матрица Н(x^*) положительно определена.

Теорема об условиях определённости матрицы.

Справедливы утверждения:

1)квадратная матрица положительно определена <=> когда все ее главные (угловые) миноры положительны

2) квадратная матрица отрицательно определена <=> когда знак любого ее главного (углового) минора каждого порядка совпадает со знаком (-1)^К

В основе метода лежат сформулированные выше теоремы о необходимых и достаточных условиях существования безусловного экстремума. Метод применим только для "достаточно гладких" (дважды непрерывно дифференцируемых функций). Метод состоит в выполнении следующих шагов.

Шаг 1. Решить уравнение (или систему уравнений ) и найти множество ее решений – стационарных точек (подозрительных на экстремум).

Шаг 2. Установить, пользуясь теоремой об условиях определенности матрицы, тип определенности матрицы Гессе в каждой стационарной точке функции , и на основе этого сделать вывод о существовании и типе экстремума

2. Элементарное преобразование СЛУ – преобразования (целенаправленные изменения) , кот оставляют СЛУ эквивалентными.

К элементарным преобразованиям относятся следующие:

1) Перестановка любых 2ух уравнений местами

2) удаление из СЛУ «пустых» уравнений вида 0х₁+0х₂+…0х_n=0

3) Умножение обоих частей в каком-либо ур-ии слу на число 0

4) Прибавление к какому-либо из уравнению слу др уравнения этой же слу, умноженного на произвольное число 0.

Эти эл-ые преобразования удобно представлять в виде эл-ых преобразований строк т.н. расширенной матрицы-системы (Ab), получаемой приписыванием к матрице А справа вектор-столбца b правой части СЛУ.

11 Теорема Кронекера-Капелли

Данная теорема отвечает на вопрос о существовании решений СЛУ.

Теорема Кронекера-Капелли СЛУ Ах=b совместна тогда и только тогда, когда ранг матрицы-системы А равен рангу расширенной матрицы-системы: r(A) =r(AB)

Расширеннаяматрица-система (Ab), получается приписыванием к матрице А справа вектор-столбца b правой части СЛУ.

Следствие: Однородная СЛУ Ах=0 имеет не нулевое решение, тогда и только тогда, когда ранг матрицы системы меньше числа её неизвестных

БИЛЕТ 9

1. Метод Крамера решения СЛУ

Этот метод предназначен для решения СЛУ в которых количество уравнений равно числу неизвестных т.е. матрица-система является квадратной.

Метод применяется только для тех СЛУ, где определитель не равен 0.

В основе метода лежит теорема Крамера:

Справедливы утверждения:

1) СЛУ Ах=b имеет единственное решение тогда и только тогда, когда │А│0

2) Если │а│0, то решение может быть найдено по формуле:

x_j=Д_j (b)/Д

где Д=│А│, Д_j (b)– это определитель матрицы-системы, в кот ее j-ый столбец заменен на столбец правой части b.

2. теор. Двойств-ти

1-я теорема двойственности:

Если одна задача двойств-ти. пары имеет решение, то и вторая тоже имеет решение, причём значения целевых ф-ций этих задач на оптим планах равны мужду собой. Если целевая ф-ция одной из задач двойствен. пары не ограничена, то множество допустимых решений второй задачи пусто, и наоборот.

2-я теорема двойственности:

План y* прямой задачи(3)(4) и план x* двойствен. задачи(1)(2) являются оптим. планами своих задач тогда и только тогда, когда выполняется соотношение:

(Σ_j=1ⁿa_ijx^*_j - b_j)y*_i = 0, i = 1, m

(Σ_i=1^ma_ijy*_i – c_j)x*_j = 0, j = 1, n

Следствие:

Если какая либо компонента оптим. плана одной из задач двойств. пары отлична от 0, то соотв. ограничение другой задачи должно выполнятся как точное равенство. Если же какое либо ограничение одной из задач выполняется как строгое неравенство, то соотв. компонента оптим. плана другой задачи этой пары равны 0.

3-я теорема двойственности

Пусть f٭=f(x٭)- значение целевой ф-ии прямой задачи на оптимальном плане x٭,тогда двойственность можно найти по соотношениям:

y*i=df٭/dbi, i=1,m

Билет 10

1. Теорема о представлении оптимального плана прямой ЗЛП. Пусть оптимальный план прямой ЗЛП (14.10)-(14.11) определяется базисными переменными (все свободные равны нулю). Тогда справедливо соотношение

(14.12)

где матрица, составленная из векторов стоящих при базисных переменных в исходной системе ограничений (14.11).

Доказательство. Собирая вместе все слагаемые левой части системы уравнений содержащие базисные переменные, имеем

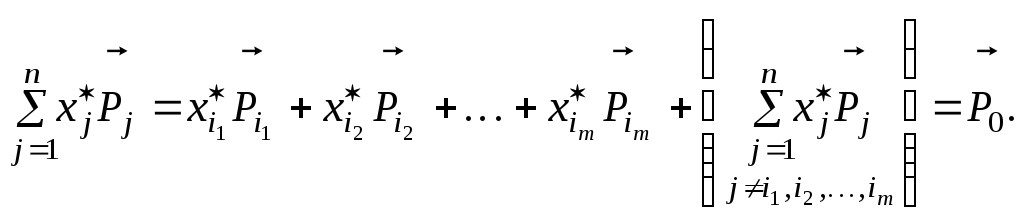(14.13)

Выражение в скобках в левой части (14.13) равно нулю, т.к. все слагаемые этого выражения равны нулю как свободные переменные (все свободные переменные в оптимальном плане ЗЛП равны нулю по теореме о вершине). Тогда из (14.13) следует

т.е.,

(14.14)

Умножая обе части (14.14) на слева, получаем что и требовалось доказать.

2. ф-ция наз-ся вогнутой (строго вогнутой), на множ-ве D, если справ-во:

(1)

ф-ия наз-ся выпуклой (строго выпуклой) на множ-ве D, ,если соотношение (1) неравенства противоположно.

Свойства выпуклых (вогнутых) функций:

1. Если f(x)- выпуклая, то –f(x) – вогнутая и наоборот.

2. Если f(x) выпукла, а >0, то ф-ция *f(x)- выпукла.

3. Сумма выпуклых ф-ций явл-ся выпуклой ф-цией.

Задача выпукло-вогнутого программирования:

Задача f(x)max(min), x D наз-ся задачей выпукло-вогнутого програм-я, если ф-ция f(x) явл-ся выпуклой при поиске min и вогнутой при поиске max, а обл-ть ограничений D предстваляет собой выпуклое множество. В задачах выпукло-вогнутого програм-я услов-е Куна-Таккера яв-ся кроме необходимым, также и достаточным.

БИЛЕТ 11

1. СЛУ и формы ее записи (представления): развернутая, матричная и векторная.

СЛУ наз любая конечная совокупность линейных уравнений.

Рассмотрим выражение Аx=b, где

a₁₁ a₁₂...a_1n

A= a₂₁ a₂₂ ...a_2n

a_m1 a_m2 ...a_mn

b₁

b₂

b= ....

b_m

x₁

x₂

x= ...

x_n

Это выражение, где матрица А- задана, правая часть (b) задана, а вектор-столбец х неизвестен, наз СЛУ в матричной форме представления.

Пользуясь операцией умножения матриц, первое выражение можно представить в виде:

а₁₁х₁+а₁₂х₂+…а_1nx_n=b₁

a₂₁x₁+a₂₂x₂+...a_2nx_n=b₂

....................................

a_m1x₁+a_m2x₂+...a_mnx_n=b_m

Это выражение представляет собой развернутую форму СЛУ.

Ещё одной формой представления СЛУ явл векторная форма записи:

_j=1ⁿA_jx_j=b здесь А_j – j-ый столбец матрицы А,

Гл задачей, связанной со СЛУ является задача ее решения.

Решением СЛУ является упорядоченный набор чисел х₁ х₂ … х_n или вектор-столбец

x₁

x₂

x= ...

x_n

который после подстановки в СЛУ обращает их в тождество.

СЛУ наз совместной если у неё есть хотя бы одно решение в противном случае эта система наз несовместной

Совместная СЛУ наз определённой, если у неё есть только одно решение и неопределённой в противном случае.