
- •1. Матрицы. Виды матриц
- •Специальные матрицы
- •2. Разложение Тейлора. Формула Тейлора с остаточным членом в форме Пеано.
- •Теорема о необходимых условиях экстремума
- •1) Перестановка любых 2ух уравнений местами
- •3) Умножение обоих частей в каком-либо ур-ии слу на число 0
- •4) Прибавление к какому-либо из уравнению слу др уравнения этой же слу, умноженного на произвольное число 0.
- •2) Если │а│0, то решение может быть найдено по формуле:
- •2 Слу наз эквивалентными или равносильными, если множества их решений совпадают.
- •Теорема об умножении определителей
- •2. Разложение Тейлора. Формула Тейлора с остаточным членом в форме Пеано.
- •Теорема о необходимых условиях экстремума
- •Ранг матрицы r(a) – это наивысший порядок отличных от 0 миноров этой матрицы
- •Теорема о производной по направлению
- •Теорема о необходимых условиях экстремума
- •2) Пусть противоречивых уравнений нет. Тогда 1 из уравнений выбирается за разрешающее уравнение и одно из неизвестных – за разрешающее неизвестное. К этому выбору предъявляются следующие требования:
- •3) Разрешающая неизвестная исключается из всех уравнений кроме разрешающего. Для этого разрешающее уравнение прибавляется к каждому из уравнений слу после умножения на подходящее число.
- •1) Реализация метода Гаусса даёт ответ на вопрос о совместности системы. Система совместна тогда и только тогда, когда при реализации метода Гаусса не возникает противоречивых уравнений
- •2) В процессе преобразований Гаусса допускаются промежуточные преобразования слу.
- •3) В любой момент преобразования Гаусса м.Б. Остановлены. Текущая система м.Б. Рассмотрена в качестве исходной и преобразования м.Б. Возобновлены по другой схеме.
- •1. Алгебраическое дополнение и минор
- •Теорема о необходимых условиях экстремума
- •2) Проводится подстановка любой точки, не лежащей на критической прямой, в текущее неравенство, тем самым определяется область «хороших» и «плохих» точек.
- •3) После выявления «хороших» полупространств для каждого неравенства производится их пересечение.
- •2) Если │а│0, то решение может быть найдено по формуле:
- •1. Понятие множества уровня функции, касательной гиперплоскости и вектора нормали к гиперплоскости.
- •1. Методы поиска обратной матрицы: метод союзной матрицы и метод элементарных преобразований.
- •2) Система s линейно-независима
- •2) Любой вектор yRn м.Б. Представлен в виде линейной комбинации векторов системы s
- •2. Экономическая интерпретация двойственных оценок
- •Метод окаймляющих миноров
- •Метод элементарных преобразований
- •Теорема об обратной матрице
- •64 Теорема о разрешимости тз:
- •1) Перестановка любых 2ух уравнений местами
- •3) Умножение обоих частей в каком-либо ур-ии слу на число 0
- •4) Прибавление к какому-либо из уравнению слу др уравнения этой же слу, умноженного на произвольное число 0.
- •2. Двойственные злп.
- •1) Перестановка любых 2ух уравнений местами
- •3) Умножение обоих частей в каком-либо ур-ии слу на число 0
- •4) Прибавление к какому-либо из уравнению слу др уравнения этой же слу, умноженного на произвольное число 0.
- •2) Пусть противоречивых уравнений нет. Тогда 1 из уравнений выбирается за разрешающее уравнение и одно из неизвестных – за разрешающее неизвестное. К этому выбору предъявляются следующие требования:
- •3) Разрешающая неизвестная исключается из всех уравнений кроме разрешающего. Для этого разрешающее уравнение прибавляется к каждому из уравнений слу после умножения на подходящее число.
- •1. Назначение и обоснование обобщенного метода множителей Лагранжа.
- •2. Открытая транспортная задача на избыток
- •26.Понятие градиента функции. Теорема о градиенте.
- •Методы поиска обратной матрицы: метод союзной матрицы и метод элементарных преобразований.
- •1. Ранг матрицы r(a) – это наивысший порядок отличных от 0 миноров этой матрицы
- •Метод окаймляющих миноров
- •Метод элементарных преобразований
Билет 1.
1. Определители. Определение и свойства определителей
Определитель – числовая функция, заданная на множестве квадратнгых матриц.
Перестановка Р={i1,i2 ,...,in} чисел (1,2, … n) – это расположение целых натуральных чисел в произвольном порядке.
Говорят, что в перестановке Р эл-ты ik,il образуют инверсию (непорядок), если выполняется условие (ik-il)(k-l)<0
Определителем │A│ квадратной матрицы An*n наз алгебраическая сумма n! слагаемых каждое из которых есть произведение n элементов матрицы А взятых по одному из каждой строки и каждого столбца, причем эти слагаемые берутся со знаком +, если число инверсий в перестановке индексов столбцов элементов этого произведения четно, и со знаком – в противном случае.
│A│=∑i1=1n∑i2=1n...∑in=1 n = a1i1*a2i2*….*anin*(-1)I (i1, i2, … , in) (i1≠i2≠…. ≠in)
Из определения следует, что определитель матрицы первого порядка будет равен │А1*1│=а11
Определители 2 и 3 порядка вычисляют по следующим из формулы схемам:
Определитель матрицы 2 порядка │А2*2│=а11*а22-а12*а21 (Разность м/у элементами главной и побочной диагонали)
Определитель матрицы 3 его порядка │А3*3│=а11*а22*а33+а12*а23*а31+а13*а21*а32-а11*а23*а32-а12*а21*а32-а13*а22*а31 (правило Сарррюса)
Свойства определителей:
1 При транспонировании матрицы её определитель не меняется │Ат│=│А│
2 Если в матрице есть нулевая строка или столбец, то её определитель равен 0
3 При перестановке 2 строк или столбцов матрицы её определитель меняет свой знак на противоположный
4 Если какую-либо строку или столбец матрицы умножить на число λ, то определитель этой матрицы будет равен λ*│А│
5 определитель матрицы не изменится, если к любой его строке или столбцу прибавить другую строку или столбец, умноженную на какое-либо число
6 Если матрица имеет 2 одинаковые строки (столбца), то определитель =0
2. Назначение и Схема реализации обобщенного метода множителей Лагранжа
Идея этого м-да
сост-т в том,что если точка безусловного
экстремума целевой ф-ии не удовл-ет всем
ограничениям задачи, то тогда решение
задачи с ограничениями должно достигаться
(если оно есть) в граничной точке области
ограничений =>одно или неск-ко огр-ий
в gi(x)
0,
![]() должны вып-ся как точные равенства (быть
активными).
должны вып-ся как точные равенства (быть
активными).
Реализация метода состоит в выполнении следующих шагов.
Шаг
1. Параметр
k
(число
учитываемых ограничений задачи)
полагается равным нулю. Исходная задача
решается без учета ограничений. Если
найденная экстремальная точка
удовлетворяет всем ограничениям исходной
задачи, то она запоминается. Параметр
k
увеличивается
на единицу:
![]() .
Переход на шаг 2.
.
Переход на шаг 2.
Шаг 2. Формируется система из k ограничений-равенств для текущей задачи: произвольные k ограничений-неравенств исходной задачи делаются «активными» посредством замены знака неравенства на знак равенства и включаются в формируемую систему ограничений. Переход на шаг 3.
Шаг 3. Полученная на предыдущем шаге текущая задача с исходной целевой функцией и системой «активных» ограничений-равенств решается каким-либо подходящим методом (например, обычным методом множителей Лагранжа). Если найденная экстремальная точка удовлетворяет ограничениям исходной задачи, то она запоминается. Переход на шаг 4.
Шаг
4. а) Если
![]() (число
активных ограничений меньше числа
ограничений исходной задачи), то
формируется такая система из k
активных
ограничений, которая еще не разу не
присутствовала в решаемых перед этим
задачах, после чего производится переход
на шаг 3. В том случае, когда все возможные
наборы из k
активных
ограничений перед этим рассматрены, а
соответствующие задачи решены, параметр
k
увеличивается
на единицу:
(число
активных ограничений меньше числа
ограничений исходной задачи), то
формируется такая система из k
активных
ограничений, которая еще не разу не
присутствовала в решаемых перед этим
задачах, после чего производится переход
на шаг 3. В том случае, когда все возможные
наборы из k
активных
ограничений перед этим рассматрены, а
соответствующие задачи решены, параметр
k
увеличивается
на единицу:
![]() .
Переход на шаг 2.
.
Переход на шаг 2.
б)
Если
![]() ,
то вычисления заканчиваются. В качестве
решения исходной задачи берется та из
запомненных на предыдущих шагах
экстремальных точек, которая дает
наибольшее (наименьшее) значение целевой
функции. При отсутствии запомненных
экстремальных точек делается вывод об
отсутствии решения исходной ЗНЛП.
,
то вычисления заканчиваются. В качестве
решения исходной задачи берется та из
запомненных на предыдущих шагах
экстремальных точек, которая дает
наибольшее (наименьшее) значение целевой
функции. При отсутствии запомненных
экстремальных точек делается вывод об
отсутствии решения исходной ЗНЛП.
Замечание 10.1.
Возможности применения метода для
решения практических задач без применения
компьютера ограничены, поскольку для
его реализации требуется вместо одной
исходной задачи решать большое число
задач с ограничениями-равенствами.
Например, если число ограничений в
(10.2)
![]() ,
а число активных ограничений
,
а число активных ограничений
![]() ,
то тогда на шаге 2 надо будет решить
,
то тогда на шаге 2 надо будет решить
![]()
задач с тремя ограничениями-равенствами.
БИЛЕТ 2
1. Матрицы. Виды матриц
Числовой матрицей Аm*n наз прямоугольная таблица чисел, состоящая из m строк и n столбцов
Числа, определяющие матрицу наз её элементами
Специальные матрицы
Матрица, имеющая 1 строку и 1 столбец наз матрицей-скаляром
Матрица, имеющая только 1 строку наз вектор-строкой
Матрица, имеющая только 1 столбец наз вектор-столбцом. А транспонируется в вектор-строку с помощью операции транспонирования и обозн-ся Ат
Матрица, у которой число строк и столбцов совпадает называют квадратной.
Произвольная матрица, все элементы которой равны 0 наз нулевой матрицей и обозначается O
Квадратная матрица, все элементы которой равны 0, за исключением элементов главной диагонали, которые равны1 наз единичной матрицей и обозначается E.
Операции над матрицами
1) Операции сравнения.
Матрицы А и В равны (А=В), если они имеют одинак размер, а все их соответств-ие элементы равны м/у собой aij= bij (i=1,m, j=1,n)
Говорят, что матрица A больше матрицы B, если матрицы имеют одинаковый размер и при этом aij>bij (i=1,m, j=1,n)
2) Операция сложения определена для любых двух матриц, имеющих одинаковый размер. Суммой С матриц А,В наз матрица А+В элементы которой определены соотношением: cij=aij+bij i=1,m j=1,n
3) Умножение матриц на число любая матрица А может быть умножена на произвольное число k, как слева так и справа в результате получается матрица С=kА=Аk, элементы которой определяются соотношением cij=kaij (i=1,m j=1,n)
Свойства:
А+В=В+А
(А+В)+С=А+(В+С) кА=Ак
к(А+В)=кА+кВ
(к+р)А=кА+рА
(кр)А=к(рА)
4) Операция вычитания определена для матриц одинакового размера. Вычитание матрицы В из Матрицы А: А-В=А+(-1)В
5) Операция произведения матриц. Произведение матриц С=А*В определено тогда и только тогда, когда количество столбцов левого сомножителя равно числу строк правого сомножителя, в результате получаем матрицу С=А*В, которая имеет столько строк, сколько левый сомножитель и столько столбцов, сколько правый сомножитель. Элементы произведения матриц определяются по формуле: сij=∑ aik*bkj, (к от 1 до р)
Свойства
(А+В)С=АС+ВС
А(В+С)=АВ+АС
А(ВС)=(АВ)С
к(ВС)=(кВ)С
АО=ОА=О
АЕ=ЕА=А
Матрица для которой А*В=В*А наз коммутативным или перестановочными
6) Операция возведения матрицы в степень определена для квадратных матриц. Пусть k- любое целое неотриц число. k-ой степенью Аk матрицы А наз матрица, опред-ая след-им образом:
E, если k=0
Ak=
Ak-1A, k>0
Свойства:
АkAp=Ak+p
(Аk)p=Akp
7) Операция транспонирования Пусть Аmxn произвольная матрица. Матрица Ат =(аji)nm, строки которой состоят из элементов столбцов матрицы А, а столбцы – из элементов строк матрицы А, назыв транспонированной матрицей А
Свойства:
(А+В)т = Ат+Вт
(А*В)т = Вт*Ат
(Ат)т = А
В специальный класс операций над матрицами выделяются следующие операции, называемые элементарными преобразованиями матриц:
1) умножение строки (столбца) матрицы на число ≠ 0
2)прибавление к элементам строки (столбца) матрицы соответствующих элементов другой её строки (столбца), умноженных на произвольное число
3) перестановка строк (столбцов) матриц местами.
!!! Любое элементарное преобразование матрицы может быть осуществлено последовательностью операций произведения этой матрицы на матрицы специального вида.
Теорема о представлении элементарных преобразований матриц операциями их умножения.
Справедливы следующие утверждения:
1) умножение i-ой строки матрицы Аmxn на число эквивалентно операции умножения L*A, где L – это квадратная матрица, где число находится в iой строке и iом столбце, все остальные элементы как в единичной матрице
(i)
100….
01000
Lmn ……. (i)
…….….
…………1 n*n
2) Прибавление к i-ой строке матрицы Аmxn ее j-ой строки, умноженной на число , эквивалентно операции умножения L*A, где L это квадратная матрица, где число находится в iой строке и jом столбце, все остальные элементы как в единичной матрице –
1 0 0 0 0 0
0 1 0 0 0 0
L(i)=0 0 1… 0 0
0 0 0 0 0
0 0 0 0 0 1
3) Перестановка строк матрицы А местами м.б. осуществлена конечной последовательностью умножений слева на эту матрицу матриц вида 1 и 2.
2. Понятие градиента функции. Теорема о градиенте.
Градиентом f(x) функции f(x) в точке y называется векторf(y), компоненты которого равны частным производным 1-ого порядка данной функции в точке y: Tf(y)=(f(y)/x1; f(y)/x2;… f(y)/xn).
Теорема о градиенте:
Градиент f(y)ф-ии f(x) указывает напр-е наискорейшего роста ф-ии f(x) в точке y. При этом максимальная скорость роста равна модулю градиента в этой точке:
Max f(y)/u=f(y)(под max написать: u Rn : u=1.
Доказательство:
Пусть - угол между векторами f(y) и u. Т.к. скалярное произведение(f(y),u) этих векторов может быть найдено по формуле
(f(y),u) =f(y)*u*cos,
а u- единичный вектор, тогда:
f(y)/u=f(y)cos .
Из этого равенства следует, что производная по направлению принимает наибольшее значение при cos =1, т.е. когда векторы f(y) и u имеют одинаковое направление. ЧТД
БИЛЕТ 3
1. Понятия частной производной функции, стационарной точки функции, градиента и матрицы Гессе.
Частной производной f’xj(z) = df(z)/dxj первого порядка функции f(x) в точке z по переменной xj наз величина: f’xj(z) = lim0 (f(z1,z2,…, zj-1, zj+j, zj+1,…zn)-f(z))/j \
Т.о. частная производная функции f(x) по переменной xj определяется точно так же как обычная производная по переменной xj при условии, что все другие переменные при этом являются const.
Говорят, что функция f(x) дифференцируема в точке zRn, если у неё в этой точке существуют все частные производные 1ого порядка по всем аргументам.
Говорят, что функция f(x) непрерывно дифференцируема в точке zRn, если все ее частные производные 1ого порядка непрерывны.
Точка zRn наз стационарной точкой функции f(x), если все частные производные 1ого порядка равны 0, т.е. f’xj(z) = 0.
Частной производной второго порядка f”xixj(z) = 2f(z)/xixj функции f(x) в точке z наз частная производная первого порядка от частной производной первого порядка.
Квадратная матрица Hnxn=(hij)nxn наз матрицей Гессе функции f(x) в точке z, если ее элементы определяются: hij= f”xixj(z).
Выражение G (H, x) = xT Hx = ∑i=1n∑j=1n hij xi xj наз квадратичной формой матрицы Hnxn=(hij)nxn
Градиентом f(x) функции f(x) в точке z наз вектор, компонентами кот являются частные производные 1ого порядка функции Tf(z)=(f’x1(z), f’x2(z),… , f’xn(z))
2.
|
прямая ЗЛП: |
|
двойственная ЗЛП: |
|
|
|
|
Нетрудно видеть, что если задачу (14.3)-(14.4) взять за прямую, то двойственной по отношению к ней будет задача (14.1)-(14.2). В связи с эти говорят, что задачи (14.1)-(14.2) и (14.3)-(14.4) образуют так называемую двойственную пару ЗЛП.
Двойственная
лемма. Для
любого плана
![]() задачи
(14.1)-(14.2) и любого плана
задачи
(14.1)-(14.2) и любого плана
![]() задачи (14.3)-(14.4)
справедливо
задачи (14.3)-(14.4)
справедливо
![]() .
.
Доказательство.
Умножим
основное ограничение
![]() задачи (14.1)-(14.2) на
задачи (14.1)-(14.2) на
![]() слева:
слева:
![]() . (14.5)
. (14.5)
Умножим основное
ограничение
![]() задачи (14.3)-(14.4) на
задачи (14.3)-(14.4) на
![]() слева:
слева:
![]() (14.6)
(14.6)
Преобразуем левую часть (14.5), используя свойства операции транспонирования:
![]() (14.7)
(14.7)
Из (14.7) следует, что
левые части (14.5) и (14.6) равны между собой.
Это означает, что
![]() что и требовалось доказать.
что и требовалось доказать.
Следствие.
Если для
некоторых планов
![]() и
и
![]() задач двойственной пары (4.25)-(4.26)
и
(4.27)-(4.28)
задач двойственной пары (4.25)-(4.26)
и
(4.27)-(4.28)
![]() то эти планы являются оптимальными
планами своих задач.
то эти планы являются оптимальными
планами своих задач.
Компоненты
![]() оптимального плана двойственной ЗЛП
(14.3)-(14.4) называются двойственными
оценками.
Двойственные оценки играют в линейном
программировании ту же роль, что и
множители Лагранжа в нелинейном
программировании.
оптимального плана двойственной ЗЛП
(14.3)-(14.4) называются двойственными
оценками.
Двойственные оценки играют в линейном
программировании ту же роль, что и
множители Лагранжа в нелинейном
программировании.
Компоненты
![]() оптимального плана прямой ЗЛП (14.1)-(14.2)
называются прямыми
оценками
оптимального плана прямой ЗЛП (14.1)-(14.2)
называются прямыми
оценками
Билет 4
1 Понятие угловой точки вып. Мног ……..
Пусть DcRn - выпуклый многогранник, точка xЄD назыв угловой точкой или вершиной D, если не сущ отрезка принадлежащего D, для которого т x явл-ся внутрен-й, это означает что не сущ y,zЄD : x=az +(1-a)*y, где 0<a<1. Точка x*ЄD назыв оптимальным планом ЗЛП, если она явл-ся точкой max или min целевой ф-ии котор требуется найти по усл задачи. Любая вершина области ограничений D ЗЛП f(x) → max (min) (xЄDcRn), назыв опорным планом этой ЗЛП
Опор. План ЗЛП назыв. Невырожд., если он содерж.ровно n положит компонент против. Случае, когда число положит. Компонент в опор. Плане < n, опор. План назыв. Вырожд.

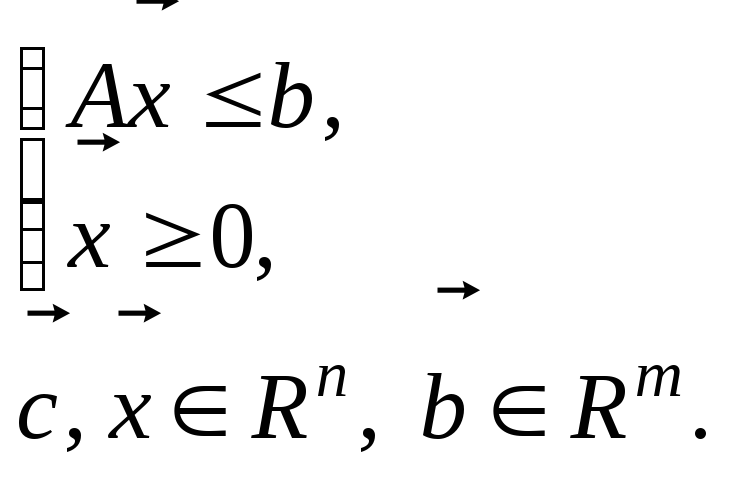 (14.2)
(14.2)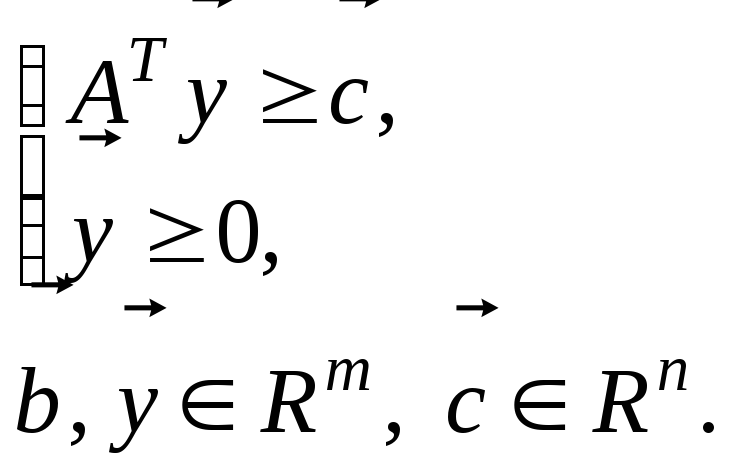 (14.4)
(14.4)