2. Двойственные злп.

Каждой ЗЛП можно поставить в соответствие другую ЗЛП, кот. называется двойственной по отношению к исходной в симметричной форме:

Прямая ЗЛП: Двойственная ЗЛП:

f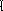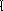(x) = c^тx → max(1) g(y) = b^тy → min(3)

Ax ≤ b (2) A^тy ≥ c(4)

x ≥ 0 y ≥ 0

c, x Є Rⁿ, b Є R^m b, y Є R^m, c Є Rⁿ

Эти задачи образуют двойственную пару ЗЛП.

______________________________________________________

Двойственная лемма:

Для любого плана х прямой задачи(1)-(2), и любого плана y двойственной задачи(3)-(4) справедливо:

f(x) ≤ g(y)

Док-во: Умножим обе части нер-ва Ax ≤ b в (2)( Ax ≤ b, x ≥ 0) на y – слева. Т. к. y>=0 следует y^тАx<= y^тb (5). Поскольку y^тb = b^тy=g(y),то тогда получается что из (5): умножим нер-во A^тy>=c на b^т- слева. Поскольку x>=0, то тогда x^т A^тy>= x^тc. Поскольку x^тс= c^тx= f(x), то тогда из послед нер-ва следует x^т A^тy>=f(x) (6). Согласно св-вам опраций умножения и транспонирования матриц имеем y^т Ax= (y^т Ax) ^т= x^т (y^тA) ^т= x^т A^тy и следует что левые части (5) (6) равны м/у собой f(x) ≤ g(y)

Следствие:

Если для некоторых планов x* и y* задач (1,2,3,4) выполняется f(x*) = g(y*), то эти планы являются оптим. Планами своих задач. Компоненты x*j,j=1,n опт. Плана х* прямой задачи (1)-(2) назыв. Прямыми. оценками, а компоненты y*_i , i = 1, n оптим. плана двойственной задачи(3)-(4) называются двойственными оценками

Билет 42

1. Понятие элементарного преобразования СЛУ и виды элементарных преобразований СЛУ

Элементарное преобразование СЛУ – преобразования (целенаправленные изменения) , которые оставляют СЛУ эквивалентными.

К элементарным преобразованиям относятся следующие:

1) Перестановка любых 2ух уравнений местами

2) удаление из СЛУ «пустых» уравнений вида 0х₁+0х₂+…0х_n=0

3) Умножение обоих частей в каком-либо ур-ии слу на число 0

4) Прибавление к какому-либо из уравнению слу др уравнения этой же слу, умноженного на произвольное число 0.

Метод Гаусса решения СЛУ

Основан на том факте, что элементарные преобразования СЛУ дают эквивалентные системы.

Метод Гаусса состоит в последовательной реализации шагов, на каждом из кот производятся следующие действия:

1) Из системы, полученной после предыдущих шагов, удаляются все пустые уравнения вида: 0х₁+0х₂+…0х_n=0

если в оставшейся системе имеется хотя бы одно противоречивое уравнение вида

0х₁+0х₂+…0х_n=b0 то исходная СЛУ несовместна, т.е. не имеет решений.

2) Пусть противоречивых уравнений нет. Тогда 1 из уравнений выбирается за разрешающее уравнение и одно из неизвестных – за разрешающее неизвестное. К этому выбору предъявляются следующие требования:

а) на предыдущих шагах выбранное уравнение не было разрешающим

б) в разрешающем уравнении коэффициент при разрешающем неизвестном должен быть отличен от 0. Этот коэффициент наз разрешающим элементом

3) Разрешающая неизвестная исключается из всех уравнений кроме разрешающего. Для этого разрешающее уравнение прибавляется к каждому из уравнений слу после умножения на подходящее число.

Преобразования заканчиваются, если ни одно из уравнений не может быть взято за разрешающее (все они перебывали в этой роли). Те неизвестные, которые в процессе преобразований были разрешающими наз базисными. Те неизвестные, которые не были разрешающими наз свободными.

Если число уравнений финальной СЛУ равно числу неизвестных, то тогда все эти неизвестные побывали в числе разрешающих и исходная СЛУ имеет единственное решение, непосредственно вытекающее из финальной СЛУ.

В случае, когда число уравнений финальной системы меньше числа неизвестных, то тогда те неизвестные, которые не были в качестве разрешающих, объявляются свободными и могут принимать любые значения.

Неизвестные, которые побывали в качестве разрешающих наз базисными. Значения базисных переменных полностью определяются свободными и непосредственно вытекают из финальной СЛУ.

Замечания:

1) Реализация метода Гаусса даёт ответ на вопрос о совместности системы. Система совместна тогда и только тогда, когда при реализации метода Гаусса не возникает противоречивых уравнений

2) В процессе преобразований Гаусса допускаются промежуточные преобразования СЛУ.

3) В любой момент преобразования Гаусса м.б. остановлены. Текущая система м.б. рассмотрена в качестве исходной и преобразования м.б. возобновлены по другой схеме.

4) реализация метода Гауса позволяет вычислить ранг матрицы исходной системы, который всегда равен числу базисгых неизвестных и числу уравнений финальной СЛУ

2. Интерпретация множителей Лагранжа. Теорема Лагранжа.

Анализируя значения множителей Лагранжа можно получить доп ценную информацию о задаче. С этим связано широкое распространение метода множителей Лагранжа. Множители Лагранжа измеряют чувствительность оптимального значения f*=f(х*) целевой функции, к изменениям const-компонент ограничений b.Что следует из теоремы.

Теорема Лагранжа:

Пусть х* - решение задачи f(x)→ min (max)

g₁(x)=b₁

………

g_m(x)=b_m

а векторы▼,,…,,определяющие строки м-цы Якоби , являются линейно независ-ми, тогда сущ-ет единств-й вектор множителей Лагранжа , удовлетворяющий сист-вместе с х* системе условий:

b – g(x) = 0,

причем = , .

Во многих экономических задачах целевая функция имеет размерность стоимости (т.е. цены, умноженной на объем продукции). С помощью ограничений вида g(x)=b устанавливаются определенные величины для затрат ресурсов. Поскольку в таких задачах с помощью множителей Лагранжа измеряют, по сути, чувствительность величины f*=f(х*), имеющей размерность стоимости, к изменениям некот кол-ва затраченного ресурса, то эти множители в этом случае имеют размерность цены. По этой причине множители Лагранжа часто называют теневыми ценами (данного вида ресурсов

БИЛЕТ 43