Производные высших порядков явно заданной функции

Рассмотрим произвольную дифференцируемую функцию у=f(х). Производная от функции у=f(х) является также функцией от x и называется производной первого порядка. Предположим, что и функция 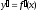дифференцируема.

Определение 3. Производной второго порядка или второй производной функции у = f(x) называется производная от ее первой производной и обозначается: , , .

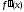Таким образом,

Аналогично производной третьего порядка или третьей производной функции у = f(x) называется производная от ее второй производной и обозначается: , , .

Таким образом,

Производной n-го порядка или n-й производной функции у = f(x) называется производная от производной (n-1)-го порядка:

Начиная с производной четвертого порядка, производные обозначаются римскими цифрами или числами в скобках.

Вторая производная имеет простой физический смысл. Пусть s=s(t) – закон движения материальной точки, тогда первая производная определяет скорость движения . Вторая производная есть скорость изменения скорости движения, т. е. ускорение .

Производные высших порядков неявно заданной функции

Пусть у=f(х) задана неявно в виде уравнения F(x, y) = 0.

Продифференцировав это уравнение по x и разрешив полученное уравнение относительно , найдем первую производную. Продифференцировав по x первую производную, найдем вторую производную от неявной функции. В нее войдут x, у и . Подставляя найденное значение в выражение второй производной, выразим через x и у.

Аналогично поступаем для нахождения производной третьего и высших порядков.

Производные высших порядков параметрически заданной функции

Пусть функция у=f(x) задана параметрическими уравнениями

Ее первая производная (если она существует) находится по формуле (6):

Поскольку вторая производная от функции y по x есть первая производная от по x, то для нахождения второй производной нужно найти первую производную от следующей параметрически заданной функции:

По формуле (6) имеем:

или

Аналогично находится третья производная от функции заданной параметрически

и т. д.

Дифференциалы высших порядков

Пусть y = f(x) дифференцируемая функция, тогда ее первый дифференциал есть также функция переменной x; можно найти дифференциал этой функции.

Определение 4. Дифференциалом второго порядка (вторым дифференциалом) функции y = f(x) называется дифференциал от первого дифференциала функции. Обозначается: или .

Так как не зависит от x, то при дифференцировании считаем постоянным:

Таким образом,

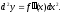
Дифференциалом третьего порядка (третьим дифференциалом) функции y = f(x) называется дифференциал от второго дифференциала функции. Обозначается: или .

Можно показать, что

Аналогично, дифференциалом n-го порядка функции y = f(x) называется дифференциал от дифференциала (n–1)-го порядка функции. Обозначается: или .

Из последнего равенства находим, В частности, при n=1, 2, 3 соответственно получаем:

т. е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

Замечание. Отметим, что все приведенные формулы для нахождения дифференциала n –го () порядка функции y = f(x), справедливы только тогда, когда x – независимая переменная. Если мы будем рассматривать функцию y = f(x), где x является функцией от какой-то другой независимой переменной, то ее дифференциалы n –го () порядков будут вычисляться по другим формулам.