Знакопеременные ряды. Общий достаточный признак сходимости знакопеременных рядов

Знакочередующийся ряд является частным случаем знакопеременного ряда.

Определение. Числовой ряд 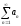, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным.

Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.

Теорема. Пусть дан знакопеременный ряд

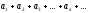. (6)

Если сходится ряд

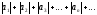, (7)

составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд (6).

Отметим, что обратное утверждение несправедливо: если сходится ряд (6), то это не означает, что будет сходиться ряд (7).

Определение. Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится. Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Функциональные ряды. Степенные ряды. Сходимость степенных рядов

Определение. Ряд, членами которого являются функции от x, называется функциональным:

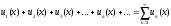. (8)

Придавая x определенное значение 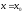, мы получим числовой ряд

,

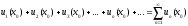который может быть как сходящимся так и расходящимся.

Если полученный числовой ряд сходится, то точка 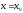называется точкой сходимости ряда (8); если же расходится – точкой расходимости функционального ряда.

Определение. Совокупность числовых значений аргумента x, при которых функциональный ряд сходится, называется его областью сходимости.

Из всех функциональных рядов простейшими и наиболее употребительными в математике и ее приложениях являются степенные ряды вида:

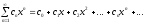. (9)

или более общего вида

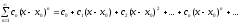
Действительные числа 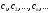называются коэффициентами ряда.

Теорема (Абеля). 1) Если степенной ряд сходится при значении 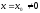, то он сходится, и притом абсолютно, при всех значениях x таких, что 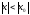. 2) Если степенной ряд расходится при 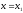, то он расходится при всех значениях x таких, что .

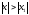Из теоремы Абеля следует, что существует такое число 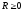, что при всех 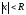ряд сходится, а при 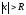– расходится. Число R называется радиусом сходимости, а нтервал (–R, R) – интервалом сходимости степенного ряда. На концах интервала сходимости, т. е. при x=–R и x=R, ряд может как сходиться, так и расходиться.

Радиус сходимости определяется по формулам

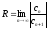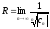или , (10)

если указанные пределы существуют.

Замечание. Если R=0, то интервал сходимости такого ряда вырождается в точку. Если же 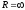, то интервал сходимости совпадает со всей числовой прямой.

Ряды Тейлора и Маклорена

Как известно, для любой функции f(x), определенной в некоторой окрестности точки 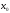и имеющей в ней производные до (n+1)-го порядка включительно, справедлива формула Тейлора:

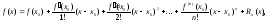(11)

где 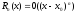остаточный член в форме Пеано. Формулу (11) кратко можно записать в виде:

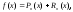
где

–

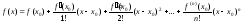многочлен Тейлора.

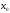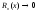Если функция f(x) имеет производные любых порядков (т. е. бесконечно дифференцируема) в окрестности точки и остаточный член при 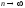, то из формулы Тейлора получается разложение функции f(x) по степеням 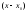, называемое рядом Тейлора:

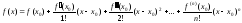. (12)

Если в ряде Тейлора положить 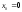, то получим разложение функции f(x) по степеням x в так называемый ряд Маклорена:

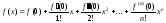. (13)

Для разложения функции f(x) в ряд Маклорена нужно:

a) найти производные ;

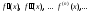б) вычислить значения производных в точке ;

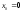в) написать разложение (13) для заданной функции и найти его интервал сходимости.

Приведем таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций:

;
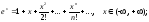
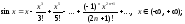
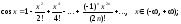
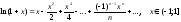