
- •GfВведение в математический анализ План
- •Множества
- •Операции над множествами
- •Понятие функции, ее области определения и множества значений. Способы задания функции
- •Основные свойства функции
- •Понятие обратной функции
- •Понятие сложной функции
- •Применение функций в экономике
- •Числовые последовательности
- •Предел последовательности
- •Число е, применение в экономике
- •Предел функции
- •Замечательные пределы
- •Бесконечно малые, бесконечно большие функции
- •Классификация бесконечно малых
- •Односторонние пределы функции
- •Непрерывность функции, классификация точек разрыва
- •Основы дифференциального исчисления функции одной переменной План
- •Определение производной
- •Геометрический и физический смысл производной
- •Связь между непрерывностью и дифференцируемостью функции
- •Правила дифференцирования функций
- •Дифференцирование сложной, обратной функций
- •Производная неявной и параметрически заданной функций
- •Определение и геометрический смысл дифференциала
- •Производные высших порядков явно заданной функции
- •Производные высших порядков неявно заданной функции
- •Производные высших порядков параметрически заданной функции
- •Дифференциалы высших порядков
- •Основные теоремы дифференциального исчисления
- •Раскрытие неопределенностей с помощью правила Лопиталя
- •Формула Тейлора
- •Разложение по формуле Маклорена некоторых элементарных функций
- •Исследование функций с помощью производных Условия возрастания и убывания функции
- •Понятие экстремума
- •Выпуклость графика функции. Точки перегиба
- •Асимптоты графика функции
- •Применение производных в экономике
- •Функция нескольких переменных План
- •Определение функции нескольких переменных. Область определения
- •Линии уровня
- •Предел функции нескольких переменных
- •Непрерывность функции нескольких переменных
- •Частные производные первого и высших порядков
- •Полный дифференциал и его применение при приближенных вычислениях
- •Дифференциалы высших порядков
- •Производная по направлению, градиент функции
- •Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции нескольких переменных в замкнутой области
- •Условный экстремум. Метод множителей Лагранжа
- •Метод наименьших квадратов
- •Основы интегрального исчисления План
- •Первообразная функции и неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •Основные методы интегрирования
- •Рациональные дроби
- •Интегрирование простейших рациональных дробей
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрический функций
- •Интегрирование некоторых иррациональных функций
- •Интегралы, не выражающиеся через элементарные функции
- •Определенный интеграл
- •Основные свойства определенного интеграла
- •Определенный интеграл с переменным верхним пределом
- •Формула Ньютона – Лейбница
- •Основные методы вычисления определенного интеграла
- •Геометрические приложения определенного интеграла
- •Некоторые приложения определенного интеграла в экономике
- •Несобственные интегралы
- •Дифференциальные уравнения План
- •Общие сведения о дифференциальных уравнениях
- •Дифференциальные уравнения первого порядка (общие понятия)
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные уравнения. Уравнения я. Бернулли
- •Дифференциальные уравнения второго порядка (основные понятия)
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения второго порядка
- •Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Применение дифференциальных уравнений в задачах экономики
- •Числовые и функциональные ряды План
- •Основные понятия. Сходимость ряда
- •Необходимый признак сходимости
- •Достаточные признаки сходимости рядов с положительными членами
- •Знакочередующиеся ряды. Признак Лейбница
- •Знакопеременные ряды. Общий достаточный признак сходимости знакопеременных рядов
- •Функциональные ряды. Степенные ряды. Сходимость степенных рядов
- •Ряды Тейлора и Маклорена
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Определение 12. Линейным дифференциальным уравнением второго порядка называется уравнение вида
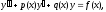 (15)
(15)
где
y
– искомая функция, а
 ,
,
 и
и
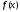 – известные функции, непрерывные на
некотором интервале (а, b).
– известные функции, непрерывные на
некотором интервале (а, b).
Если
 ,
то уравнение (15) называется линейным
однородным
уравнением. Если же функция
,
то уравнение (15) называется линейным
однородным
уравнением. Если же функция
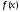 не равна тождественно нулю, то уравнение
(15) называется линейным
неоднородным
уравнением. Если разрешить уравнение
(15) относительно второй производной, то
легко видеть, что оно является частным
случаем уравнения
не равна тождественно нулю, то уравнение
(15) называется линейным
неоднородным
уравнением. Если разрешить уравнение
(15) относительно второй производной, то
легко видеть, что оно является частным
случаем уравнения
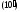 и
удовлетворяет условиям теоремы Коши.
Поэтому для любых начальных условий
(11) это уравнение имеет единственное
решение задачи Коши.
и
удовлетворяет условиям теоремы Коши.
Поэтому для любых начальных условий
(11) это уравнение имеет единственное
решение задачи Коши.
Рассмотрим
частный случай уравнения (15), когда
функции
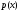 и
и
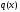 – постоянные величины, т. е.
– постоянные величины, т. е.

Уравнение такого вида называется линейным уравнением с постоянными коэффициентами.
Линейные однородные уравнения второго порядка
Рассмотрим линейное однородное уравнение второго порядка
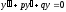 ,
(16)
,
(16)
где p и q – вещественные числа.
Можно
показать, что при определенных условиях
функция
 ,
где k
–некоторое число, является
решением уравнения (16). Действительно,
подставляя функцию
,
где k
–некоторое число, является
решением уравнения (16). Действительно,
подставляя функцию
 и
ее производные
и
ее производные
 в уравнение (16), получим
в уравнение (16), получим
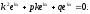
Сокращая
обе части этого равенства на
 ,
получаем квадратичное уравнение
относительно k
,
получаем квадратичное уравнение
относительно k
 .
(17)
.
(17)
Уравнение
(17) называется характеристическим
уравнением
для уравнения (16). Заметим, что если число
 является корнем уравнения (17), то функция
является корнем уравнения (17), то функция
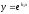 есть решение однородного уравнения
(16). Таким
образом, в зависимости от корней
есть решение однородного уравнения
(16). Таким
образом, в зависимости от корней
 и
и
 характеристического уравнения (17)
получаем общее решение уравнения (16).
Таким образом, справедлива следующая
характеристического уравнения (17)
получаем общее решение уравнения (16).
Таким образом, справедлива следующая
Теорема
3.
1. Если корни характеристического
уравнения (17) различные действительные
числа, т. е.
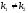 ,
то общее решение однородного
дифференциального уравнения (16) имеет
вид
,
то общее решение однородного
дифференциального уравнения (16) имеет
вид
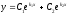 ;
;
2.
Если корни уравнения (17) равные
действительные числа, т. е.
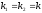 ,
то общее решение однородного
дифференциального уравнения (16) имеет
вид
,
то общее решение однородного
дифференциального уравнения (16) имеет
вид
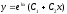 ;
;
3.
Если корни уравнения (17) комплексные,
т. е.
 ,
то общее решение однородного
дифференциального уравнения (16) имеет
вид
,
то общее решение однородного
дифференциального уравнения (16) имеет
вид
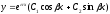 .
.
Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид
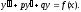 (18)
(18)
Теорема 4. Общее решение неоднородного уравнения (18) состоит из суммы его частного решения и общего решения соответствующего однородного уравнения.
Таким образом, общее решение уравнения (18) находится по формуле
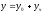 ,
(19)
,
(19)
где
 –
общее решение соответствующего
однородного уравнения
–
общее решение соответствующего
однородного уравнения
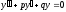 ,
,
а
 –
частное решение неоднородного уравнения
(18).
–
частное решение неоднородного уравнения
(18).
Укажем способы нахождения частного решения в случае, когда правая часть уравнения (18) имеет специальный вид.
1. Если
 ,
,
где
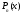 – многочлен степени n,
тогда частное решение будем искать в
виде
– многочлен степени n,
тогда частное решение будем искать в
виде
 ,
,
где
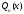 – многочлен степени n
с неопределенными коэффициентами; r=0,
если
– многочлен степени n
с неопределенными коэффициентами; r=0,
если
 не является корнем характеристического
уравнения; если же
не является корнем характеристического
уравнения; если же
 является корнем характеристического
уравнения, то r
равно кратности этого корня.
является корнем характеристического
уравнения, то r
равно кратности этого корня.
2. Если
 ,
,
где
 – многочлены степени n
и
m
соответственно,
тогда частное решение будем искать в
виде
– многочлены степени n
и
m
соответственно,
тогда частное решение будем искать в
виде
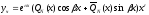 ,
,
где
 – многочлены степени
– многочлены степени
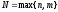 с неопределенными коэффициентами; r=0,
если
с неопределенными коэффициентами; r=0,
если
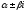 не является корнем характеристического
уравнения; если же
не является корнем характеристического
уравнения; если же
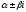 является корнем характеристического
уравнения, то r
равно кратности этого корня.
является корнем характеристического
уравнения, то r
равно кратности этого корня.
