
- •GfВведение в математический анализ План
- •Множества
- •Операции над множествами
- •Понятие функции, ее области определения и множества значений. Способы задания функции
- •Основные свойства функции
- •Понятие обратной функции
- •Понятие сложной функции
- •Применение функций в экономике
- •Числовые последовательности
- •Предел последовательности
- •Число е, применение в экономике
- •Предел функции
- •Замечательные пределы
- •Бесконечно малые, бесконечно большие функции
- •Классификация бесконечно малых
- •Односторонние пределы функции
- •Непрерывность функции, классификация точек разрыва
- •Основы дифференциального исчисления функции одной переменной План
- •Определение производной
- •Геометрический и физический смысл производной
- •Связь между непрерывностью и дифференцируемостью функции
- •Правила дифференцирования функций
- •Дифференцирование сложной, обратной функций
- •Производная неявной и параметрически заданной функций
- •Определение и геометрический смысл дифференциала
- •Производные высших порядков явно заданной функции
- •Производные высших порядков неявно заданной функции
- •Производные высших порядков параметрически заданной функции
- •Дифференциалы высших порядков
- •Основные теоремы дифференциального исчисления
- •Раскрытие неопределенностей с помощью правила Лопиталя
- •Формула Тейлора
- •Разложение по формуле Маклорена некоторых элементарных функций
- •Исследование функций с помощью производных Условия возрастания и убывания функции
- •Понятие экстремума
- •Выпуклость графика функции. Точки перегиба
- •Асимптоты графика функции
- •Применение производных в экономике
- •Функция нескольких переменных План
- •Определение функции нескольких переменных. Область определения
- •Линии уровня
- •Предел функции нескольких переменных
- •Непрерывность функции нескольких переменных
- •Частные производные первого и высших порядков
- •Полный дифференциал и его применение при приближенных вычислениях
- •Дифференциалы высших порядков
- •Производная по направлению, градиент функции
- •Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции нескольких переменных в замкнутой области
- •Условный экстремум. Метод множителей Лагранжа
- •Метод наименьших квадратов
- •Основы интегрального исчисления План
- •Первообразная функции и неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •Основные методы интегрирования
- •Рациональные дроби
- •Интегрирование простейших рациональных дробей
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрический функций
- •Интегрирование некоторых иррациональных функций
- •Интегралы, не выражающиеся через элементарные функции
- •Определенный интеграл
- •Основные свойства определенного интеграла
- •Определенный интеграл с переменным верхним пределом
- •Формула Ньютона – Лейбница
- •Основные методы вычисления определенного интеграла
- •Геометрические приложения определенного интеграла
- •Некоторые приложения определенного интеграла в экономике
- •Несобственные интегралы
- •Дифференциальные уравнения План
- •Общие сведения о дифференциальных уравнениях
- •Дифференциальные уравнения первого порядка (общие понятия)
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные уравнения. Уравнения я. Бернулли
- •Дифференциальные уравнения второго порядка (основные понятия)
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения второго порядка
- •Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Применение дифференциальных уравнений в задачах экономики
- •Числовые и функциональные ряды План
- •Основные понятия. Сходимость ряда
- •Необходимый признак сходимости
- •Достаточные признаки сходимости рядов с положительными членами
- •Знакочередующиеся ряды. Признак Лейбница
- •Знакопеременные ряды. Общий достаточный признак сходимости знакопеременных рядов
- •Функциональные ряды. Степенные ряды. Сходимость степенных рядов
- •Ряды Тейлора и Маклорена
GfВведение в математический анализ План
Множества. Понятие функции, ее области определения и множества значений. Способы задания функции. Основные свойства функции. Понятие обратной, сложной функции. Приложение функций в экономике.
Числовые последовательности. Предел последовательности. Число е, применение в экономике (формулы сложных и непрерывных процентов).
Предел функции. Замечательные пределы. Бесконечно малые и бесконечно большие функции, сравнение бесконечно малых. Односторонние пределы функций. Непрерывность функций, классификация точек разрыва.
Множества
Понятие множества считается первоначальным, неопределенным.
Определение 1. Под множеством будем понимать совокупность каких-либо объектов произвольной природы.
Объекты или предметы, из которых состоят множества, называются элементами множества.
Множества обозначают прописными латинскими буквами А, В, …, X, У, …, а элементы множества – строчными латинскими буквами а, b, …, x, y, … .
Если
элемент x
является
элементом множества А,
то пишут
 ,
если y
не является элементом множества А,
то пишут
,
если y
не является элементом множества А,
то пишут
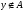 .
.
Определение 2. Множество, не содержащее ни одного элемента, называется пустым и обозначается .
Элементы
множества записывают в фигурных скобках,
внутри которых они перечислены (если
это возможно), либо указано общее
свойство, которым обладают все элементы
данного множества. Например, запись
А={1,
2, 3} означает, что множество состоит из
элементов 1, 2 и 3; запись
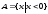 означает, что множество А
состоит из всех действительных (если
не оговорено иное) отрицательных чисел.
означает, что множество А
состоит из всех действительных (если
не оговорено иное) отрицательных чисел.
Определение 3. Множество А называется подмножеством множества В, если каждый элемент множества А принадлежит множеству В.
Обозначается .
.
Определение 4. Два множества называются равными, если они состоят из одних и тех же элементов.
Равенство
множеств А
и В
обозначается .
.
Операции над множествами
1.
Объединением
множеств А
и В
называется
множество
 ,
содержащее те и только те элементы,
которые принадлежит хотя бы одному из
множеств А
или В.
,
содержащее те и только те элементы,
которые принадлежит хотя бы одному из
множеств А
или В.
 .
.
2.
Пересечением
множеств А
и В называется
множество ,
содержащее те и только те элементы,
которые принадлежат обоим множествам
одновременно.
,
содержащее те и только те элементы,
которые принадлежат обоим множествам
одновременно.
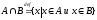 .
.
3.
Разностью
множеств А
и В называется
множество
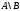 ,
содержащее те и только те элементы
множества А,
которые не принадлежат множеству В.
,
содержащее те и только те элементы
множества А,
которые не принадлежат множеству В.
 .
.
4.
Декартовым
произведением множеств
А
и В
называется множество
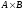 ,
содержащее всевозможные упорядоченные
пары (x,y),
где
,
содержащее всевозможные упорядоченные
пары (x,y),
где
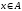 ,
,
 .
.
 .
.
Замечание.
Если
А=В,
то
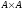 называется декартовым
квадратом
и обозначается
называется декартовым
квадратом
и обозначается
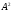 ,
т.е.
,
т.е.
 .
.
Пример. Рассмотрим числовые множества:
1. N={1, 2, 3, …, n, …} – множество натуральных чисел;
2. Z={ …, –2, –1, 0, 1, 2, …, } – множество целых чисел;
3.
Q=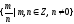 – множество рациональных чисел;
– множество рациональных чисел;
4. R – множество действительных чисел.
Между
этими множествами существует соотношение:
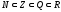 .
.
Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью.
Действительные числа, не являющиеся рациональными, называются иррациональными.
